【スマホで読む・わかりやすい】センター数学IIB2020追試【解説・正解・問題】

第２問

正解と解説

ア 3　イ,ウ 3,1　エオ 10
カ 3　キ 2　ク,ケ a, 1
コサ,シ －2, 3
スセソ,タチ －41, 27
ツ 2　テトナ －11
ニ 3　ヌネ －3

(1)

$f(x)$ を $x$ で微分すると
$f'(x)=3x^2$
したがって
$f'(-1)=3$

・・・ア

直線 $\ell$ は，点A$(-1,-2)$ を通り，傾きが 3 の直線だから，その方程式は
$y+2=3(x+1)$
$y=3(x+1)-2$
$=3x+3-2$
$=3x+1$

・・・イウ

式を変形すると
$3x-y+1=0$
点と直線の距離を求める公式を求めて，直線 $\ell$ と原点(0,0)の距離 $d$ を求めると
$d=\cfrac{|3\cdot0-1\cdot0+1|}{\sqrt{3^2+1^2}}$
$=\cfrac{1}{\sqrt{10}}=\cfrac{\sqrt{10}}{10}$

・・・エオ

(2)

曲線 $C_2$ の $x=1$ における接線の傾きは直線 $\ell$ と一致するので
$g'(-1)=3$

・・・カ

ここで，$g(x)$ を $x$ で微分すると
$g'(x)=3x^2+2ax+b$
となるので
$g'(-1)=3-2a+b=3$
$2a-b=0$
$b=2a$

・・・キ

また，$C_2$ は点Aを通るので
$g(-1)=(-1)^3+a(-1)^2+b(-1)+c$
$=-1+a-b+c=-2$
$a-b+c=-1$
$b=2a$ を代入すると
$a-2a+c=-1$
$c=a-1$

・・・クケ

(3)

(2)より
$g(x)=x^3+ax^2+bx+c$
$=x^3+ax^2+2ax+a-1$
$a=-2$ を代入すると
$g(x)=x^3-2x^2-4x-2-1$
$=x^3-2x^2-4x-3$
$g(x)$ を $x$ で微分すると
$g'(x)=3x^2-4x-4$
$3x^2-4x-4=0$ とすると
$(3x+2)(x-2)=0$
$x=-\cfrac{2}{3},\enspace2$
増減表は

$\def\arraystretch{1.25}\begin{array}{c||c|c|c|c|c}x&\cdots&-\frac{2}{3}&\cdots&2&\cdots\\\hline g'(x)&+&0&-&0&+\\\hline g(x)&\nearrow&\text{極大}&\searrow&\text{極小}&\nearrow\end{array}$

したがって，極大値は
$g\Big(-\cfrac{2}{3}\Big)=\Big(-\cfrac{2}{3}\Big)^3-2\Big(-\cfrac{2}{3}\Big)^2-4\Big(-\cfrac{2}{3}\Big)-3$
$=-\cfrac{8}{27}-\cfrac{8}{9}+\cfrac{8}{3}+3$
$=\cfrac{-8-24+72-81}{27}$
$=\cfrac{-41}{27}$

・・・スセソタチ

また，極小値は
$g(2)=2^3-2\cdot2^2-4\cdot2-3$
$=-11$

・・・テトナ

(4)

グラフが $x$ 軸より下側にあるので，そのまま積分すると面積がマイナスの値になってしまう。そのため，式にマイナスの符号をつけることに注意すると
$\displaystyle S_1=\int_{-2}^{-1}-\Big\{g(x)-f(x)\Big\}dx$
$\displaystyle =\int_{-2}^{-1}\Big\{f(x)-g(x)\Big\}dx$
$\displaystyle S_2=\int_{-1}^{1}-\Big\{g(x)-f(x)\Big\}dx$
$\displaystyle =\int_{-1}^{1}\Big\{f(x)-g(x)\Big\}dx$
したがって
$S=S_1+S_2$
$\displaystyle=\int_{-2}^1\Big\{f(x)-g(x)\Big\}dx$

・・・ニ

これを計算すると
$\displaystyle S=\int_{-2}^1\Big\{f(x)-g(x)\Big\}dx$
$\displaystyle=\int_{-2}^1 x^3-1-(x^3+ax^2+2ax+a-1)dx$
$\displaystyle=\int_{-2}^1 -ax^2-2ax-a\space dx$
$\displaystyle=-a\int_{-2}^1 x^2+2x+1\space dx$
$=-a\Big[\cfrac{x^3}{3}+x^2+x\Big]_{-2}^1$
$=-a\Big\{\cfrac{1}{3}+1+1-\Big(-\cfrac{8}{3}+4-2\Big)\Big\}$
$=-a\Big(\cfrac{1}{3}+2+\cfrac{8}{3}-2\Big)$
$=-3a$

・・・ヌネ

問題文

$a,b,c$ を実数とし，関数 $f(x)=x^3-1$，$g(x)=x^3+ax^2+bx+c$ を考える。座標平面上の曲線 $y=f(x)$ を $C_1$ とし，曲線 $y=g(x)$ を $C_2$ とする。$C_2$ は点 A$(-1,-2)$ を通り，$C_2$ の A における接線は $C_1$ の A における接線と一致するものとする。
(1) 曲線 $C_1$ の点 A における接線を $\ell$ とする。$f'(-1)=\boxed{\text{ ア }}$ により，$\ell$ の方程式は $y=\boxed{\text{ イ }}\space x+\boxed{\text{ ウ }}$ である。また，原点 O と直線 $\ell$ の距離は $\cfrac{\sqrt{\boxed{\text{ エオ }}}}{\boxed{\text{ エオ }}}$ である。
(2) 曲線 $C_2$ の点 A における接線は(1)の直線 $\ell$ と一致しているので，$g'(-1)=\boxed{\text{ カ }}$ である。したがって，$b,c$ を $a$ を用いて表すと，$b=\boxed{\text{ キ }}\space a,c=\boxed{\text{ ク }}-\boxed{\text{ ケ }}$ である。
(3) $a=-2$ のとき，関数 $g(x)$ は $x=\cfrac{\boxed{\text{ コサ }}}{\boxed{\text{ シ }}}$ で極大値 $\cfrac{\boxed{\text{ スセソ }}}{\boxed{\text{ タチ }}}$ をとり，$x=\boxed{\text{ ツ }}$ で極小値 $\boxed{\text{ テトナ }}$ をとる。
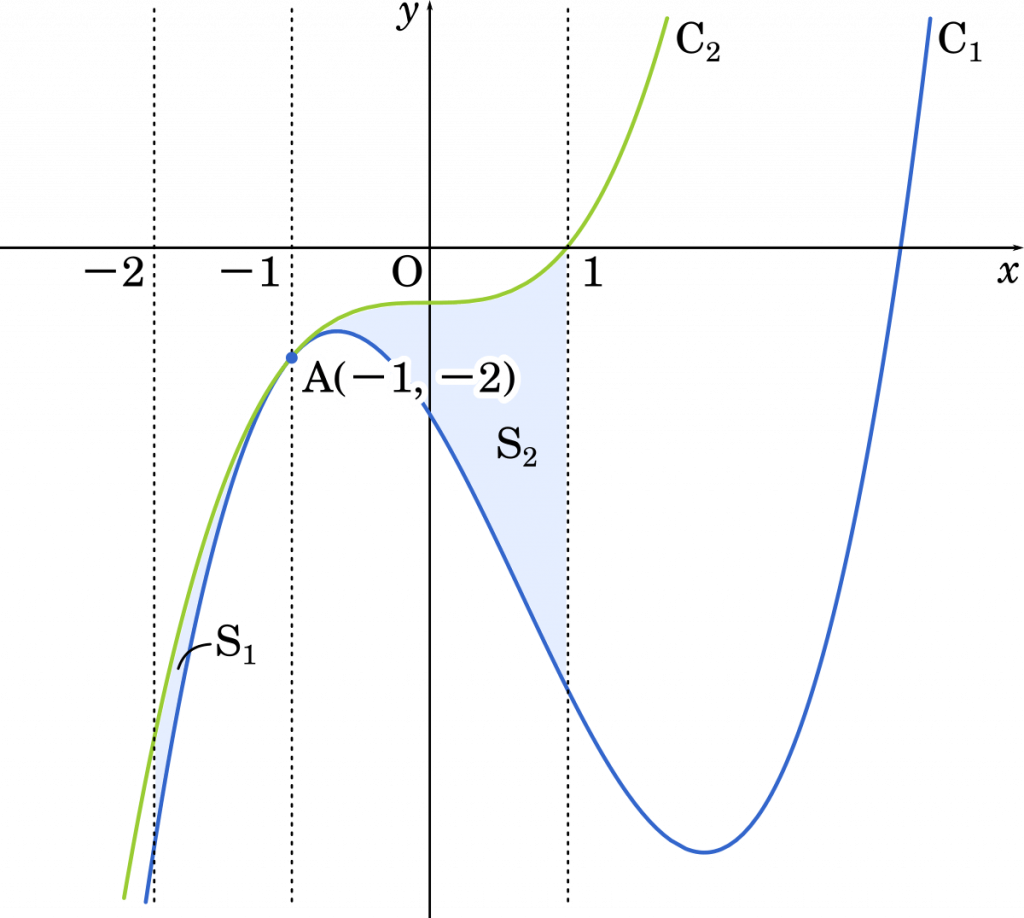
(4) $a < 0$ とする。$-2\leqq x \leqq -1$ において，曲線 $C_1$ と $C_2$ および直線 $x=-2$ で囲まれた図形の面積を $S_1$ とする。また，$-1\leqq x\leqq 1$ において，曲線 $C_1$ と $C_2$ および直線 $x=1$ で囲まれた図形の面積を $S_2$ とする。このとき，$S=S_1+S_2$ とおくと，$S=\boxed{\text{ ニ }}$ と表される。$\boxed{\text{ ニ }}$ に当てはまるものを，次の⓪～③のうちから一つ選べ。
⓪ $\displaystyle\int_{-2}^{-1}\{g(x)-f(x)\}dx+\int_{-1}^{1}\{f(x)-g(x)\}dx$
① $\displaystyle\int_{-2}^{-1}\{f(x)-g(x)\}dx+\int_{-1}^{1}\{g(x)-f(x)\}dx$
② $\displaystyle\int_{-2}^{1}\{g(x)-f(x)\}dx$
③ $\displaystyle\int_{-2}^{1}\{f(x)-g(x)\}dx$
これを計算することにより，$S=\boxed{\text{ ヌネ }}\space a$