【スマホで読む・わかりやすい】センター数学IIB2020本試【解説・正解・問題】

第4問　解答・解説

ア イ 3 6　ウ エ 4 3　オカ 36

キク ケ －2 3　コ 1　サ シ 2 6

ス,セ,ソタ 2, 2, －4

チ 3　ツテ 30

ト ナ ニ 1 2 2

ヌ ネ ノ 1 2 2　ハヒ 60

フ 3　ヘ ホ 4 3

(1)

$|\overrightarrow{\text{OA}}|=\sqrt{3^2+3^2+(-6)^2}=3\sqrt{6}$

…アイ

$|\overrightarrow{\text{OB}}|=\sqrt{(2+2\sqrt{3})^2+(2-2\sqrt{3})^2+(-4)^2}$

$=\sqrt{4+8\sqrt{3}+12+4-8\sqrt{3}+12+16}$

$=4\sqrt{3}$

…ウエ

成分表示による内積の公式 $\vec{a}\cdot\vec{b}=x_1x_2+y_1y_2+z_1z_2$ を用いて

$\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OB}}=3(2+2\sqrt{3})+3(2-2\sqrt{3})+(-6)(-4)$

$=6+6\sqrt{3}+6-6\sqrt{3}+24$

$=36$

…オカ

(2)

$\overrightarrow{\text{OC}}=s\overrightarrow{\text{OA}}+t\overrightarrow{\text{OB}}$，$\overrightarrow{\text{OA}}$⊥$\overrightarrow{\text{OC}}$ より $\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OC}}=0$ だから

$\overrightarrow{\text{OA}}(s\overrightarrow{\text{OA}}+t\overrightarrow{\text{OB}})=0$

$s|\overrightarrow{\text{OA}}|^2+t\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OB}}=0$

(1)より $|\overrightarrow{\text{OA}}|=3\sqrt{6}$，$\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OB}}=36$ だから

$54s+36t=0$

$3s+2t=0$

また①より

$\overrightarrow{\text{OB}}\cdot\overrightarrow{\text{OC}}=24$

$\overrightarrow{\text{OB}}(s\overrightarrow{\text{OA}}+t\overrightarrow{\text{OB}})=24$

$s\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OB}}+t|\overrightarrow{\text{OB}}|^2=24$

(1)より，$|\overrightarrow{\text{OB}}|=4\sqrt{3}$ だから

$36s+48t=24$

$3s+4t=2$

ここで，$3s+2t=0$ と $3s+4t=2$ を連立して

$2t=2$

$t=1$

…コ

$3s+2\cdot1=0$

$3s=-2$

$s=\cfrac{-2}{3}$

…キク，ケ

さらに $|\overrightarrow{\text{OC}}|$ を求めると

$\overrightarrow{\text{OC}}=-\cfrac{2}{3}\overrightarrow{\text{OA}}+\overrightarrow{\text{OB}}$

$=-\cfrac{2}{3}(3,3,-6)+(2+\sqrt{3},2-2\sqrt{3},-4)$

$=(-2,-2,4)+(2+2\sqrt{3},2-2\sqrt{3},-4)$

$=(2\sqrt{3},-2\sqrt{3},0)$

$|\overrightarrow{\text{OC}}|=\sqrt{(2\sqrt{3})^2+(-2\sqrt{3})^2+0^2}$

$=2\sqrt{6}$

…サシ

(3)

$\overrightarrow{\text{CB}}=\overrightarrow{\text{OB}}-\overrightarrow{\text{OC}}$

$=(2+2\sqrt{3},2-2\sqrt{3},-4)-(2\sqrt{3},-2\sqrt{3},0)$

$=(2,2,-4)$

…スセソタ

さらに $|\overrightarrow{\text{CB}}|$ を求めると

$|\overrightarrow{\text{CB}}|=\sqrt{2^2+2^2+(-4)^2}=2\sqrt{6}$

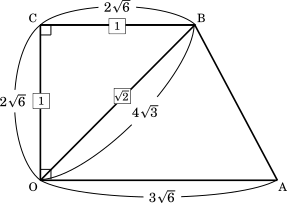
ここで

OB : OC = $4\sqrt{3}:2\sqrt{6}$

$2\sqrt{3}$ で割ると

$=2:\sqrt{2}$

$\sqrt{2}$ をかけると

$=2\sqrt{2}:2$

$=\sqrt{2}:1$

つまり，△OBC は辺の長さの比が $1:1:\sqrt{2}$ の直角二等辺三角形であることが分かる。したがって，OC ⊥ CB だから，四角形 OABC は台形である。

…チ

台形の面積を求めると

$S=\cfrac{1}{2}(2\sqrt{6}+3\sqrt{6})\cdot2\sqrt{6}=30$

…ツテ

(4)

点 D の座標を $(x,y,1)$ とおくと，$\overrightarrow{\text{OA}}$⊥$\overrightarrow{\text{OD}}$ だから

$\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OD}}=0$

$3x+3y-6=0$

$x+y=2$

また

$\overrightarrow{\text{OC}}\cdot\overrightarrow{\text{OD}}=2\sqrt{6}$

$2\sqrt{3}x-2\sqrt{3}y+0\cdot1=2\sqrt{6}$

$x-y=\sqrt{2}$

式を連立して

$2x=2+\sqrt{2}$

$x=1+\cfrac{\sqrt{2}}{2}$

$x+y=2$ に代入して

$1+\cfrac{\sqrt{2}}{2}+y=2$

$y=1-\cfrac{\sqrt{2}}{2}$

したがって，点 D の座標は

$\bigg(1+\cfrac{\sqrt{2}}{2},1-\cfrac{\sqrt{2}}{2},1\bigg)$

…トナニヌネノ

次に ∠COD を求めると

$|\overrightarrow{\text{OD}}|=\sqrt{\bigg(1+\cfrac{\sqrt{2}}{2}\bigg)^2+\bigg(1-\cfrac{\sqrt{2}}{2}\bigg)^2+1^2}$

$=\sqrt{1+\sqrt{2}+\cfrac{1}{2}+1-\sqrt{2}+\cfrac{1}{2}+1}$

$=\sqrt{4}=2$

$\overrightarrow{\text{OC}}\cdot\overrightarrow{\text{OD}}=|\overrightarrow{\text{OC}}||\overrightarrow{\text{OD}}|\cos\angle\text{COD}=2\sqrt{6}$

$2\sqrt{6}\cdot2\cos\angle\text{COD}=2\sqrt{6}$

$\cos\angle\text{COD}=\cfrac{1}{2}$

$\angle\text{COD}=60\degree$

さらに四面体 DABC を考えると，OD から垂線を下ろし OC と交わる点を H とすると，∠COD = $60\degree$，OD = $2$ より，DH = $\sqrt{3}$ であることが分かる。

…フ

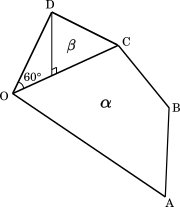
また，△ABC の面積を求めると

△ABC=$30-$△OAC=$30-\cfrac{1}{2}\cdot3\sqrt{6}\cdot2\sqrt{6}=30-18=12$

四面体の体積を求めると

$V=\cfrac{1}{3}\cdot12\cdot\sqrt{3}=4\sqrt{3}$

…ヘホ

第4問　問題文

点 O を原点とする座標空間に 2 点

A$(3,3, -6)$, B$(2 + 2\sqrt{3}, 2-2\sqrt{3}, -4)$

をとる。3点 O, A, B の定める平面を $\alpha$ とする。また, $\alpha$ に含まれる点 C は

$\overrightarrow{\text{OA}}$⊥$\overrightarrow{\text{OC}}$, $\overrightarrow{\text{OB}}\cdot\overrightarrow{\text{OC}}=24\cdots\cdots$①

を満たすとする。

(1) $|\overrightarrow{\text{OA}}|=\boxed{\text{ア}}\sqrt{\boxed{\text{イ}}}$, $|\overrightarrow{\text{OB}}|=\boxed{\text{ウ}}\sqrt{\boxed{\text{エ}}}$ である。

(2) 点 C は平面 $\alpha$ 上にあるので, 実数 $s, t$ を用いて, $\overrightarrow{\text{OC}}=s\overrightarrow{\text{OA}}+t\overrightarrow{\text{OB}}$ と表すことができる。このとき, ① からである。したがって, $|\overrightarrow{\text{OC}}|=\boxed{\text{サ}}\sqrt{\boxed{\text{シ}}}$ である。

(3) $\overrightarrow{\text{CB}}=(\boxed{\text{ス}},\boxed{\text{セ}},\boxed{\text{ソタ}})$ である。したがって,平面 $\alpha$ 上の四角形 OABC は $\boxed{\text{チ}}$。$\boxed{\text{チ}}$ に当てはまるものを, 次の ⓪~④ のうちから一つ選べ。ただし, 少なくとも一組の対辺が平行な四角形を台形という。

⓪ 正方形である

① 正方形ではないが, 長方形である

② 長方形ではないが,平行四辺形である

③ 平行四辺形ではないが,台形である

④ 台形ではない

$\overrightarrow{\text{OA}}$⊥$\overrightarrow{\text{OC}}$ であるので, 四角形 OABC の面積は $\boxed{\text{ツテ}}$ である。

(4) $\overrightarrow{\text{OA}}$⊥$\overrightarrow{\text{OD}}$, $\overrightarrow{\text{OC}}\cdot\overrightarrow{\text{OD}} = 2\sqrt{6}$ かつ $z$ 座標が $1$ であるような点 D の座標は

$\bigg(\boxed{\text{ト}}+\cfrac{\sqrt{\boxed{\text{ナ}}}}{\boxed{\text{ニ}}},\boxed{\text{ヌ}}-\cfrac{\sqrt{\boxed{\text{ネ}}}}{\boxed{\text{ノ}}},1\bigg)$

である。このとき ∠COD = $\boxed{\text{ハヒ}}$ である。

3点 O, C, D の定める平面を $\beta$ とする。$\alpha$ と $\beta$ は垂直であるので, 三角形 ABC を底面とする四面体 DABC の高さは $\sqrt{\boxed{\text{フ}}}$ である。したがって, 四面体 DABC の体積は $\boxed{\text{ヘ}}\sqrt{\boxed{\text{ホ}}}$ である。