第2問 解答・解説
ア イ 2 2 ウ 1 エ オ カ 2 4 2
キ ク 4 1 ケ,コ 0,2
サ シ 2 1 ス a セ ソ 3 3
タ 1 チ ツ 1 3
テ,ト,ナ,ニ ヌ 2,4,2,1 3
ネ ノ 2 3 ハ ヒフ 2 27
(1)
C:y=x2+2x+1 を x で微分すると
y’=2x+2=2(x+1)
x=t における接線の傾きは 2t+2 となる。
これが点(t,t2+2t+1) を通るので,ℓ の方程式は
y−t2−2t−1=(2t+2)(x−t)
y=(2t+2)x−t(2t+2)+t2+2t+1
y=(2t+2)x−t2+1⋯⋯①
…アイウ
また f(x) を x で微分すると
f′(x)=2x−4a+2
x=s における接線の傾きは 2s−4a+2 となる。
これが点(s,f(s)) を通るので,ℓ の方程式は
y−f(s)=(2s−4a+2)(x−s)
y=(2s−4a+2)x−s(2s−4a+2)+f(s)
=(2s−4a+2)x−2s2+4as−2s+s2−(4a−2)s+4a2+1
=(2s−4a+2)x−s2+4a2+1⋯⋯②
…エオカキク
①,② を比べると
2t+2=2s−4a+2
2t=2s−4a
t=s−2a
また
−t2+1=−s2+4a2+1
t2=s2−4a2
これに t=s−2a を代入して
(s−2a)2=s2−4a2
s2−4as+4a2=s2−4a2
4as=8a2
s=2a
…コ
よって
t=s−2a=2a−2a
t=0
…ケ
これを ① に代入して
ℓ:y=2x+1
…サシ
(2)
C,D を連立すると
x2−(4a−2)x+4a2+1=x2+2x+1
−(4a−2)x+4a2=2x
4ax=4a2
x=a
…ス
また,
S=∫0ax2+2x+1−2x−1 dx
=∫0ax2 dx
=[3x3]0a=3a3
…セソ

(3)

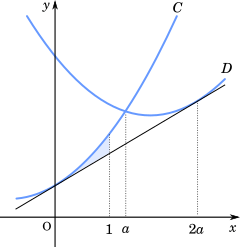
図より,a > 1 のとき,求める面積は一定であることが分かる。このとき,
T=∫01x2+2x+1−2x−1 dx
=[3x3]01=31
…チツ
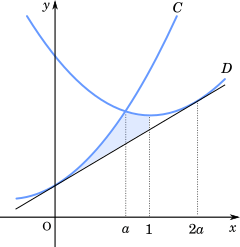
また,21≦a≦1 のとき

T=S+∫a1x2−(4a−2)x+4a2+1−2x−1 dx
T=3a3+∫a1x2−4ax+4a2 dx
=3a3+[3x3−2ax2+4a2x]a1
=3a3+(31−2a+4a2)−(3a3−2a3+4a3)
=−2a3+4a2−2a+31
…チツ
(4)
U=2T−3S
=−4a3+8a2−4a+32−a3
=−5a3+8a2−4a+32
g(a)=−5a3+8a2−4a+32 として
g′(a)=−15a2+16a−4
−15a2+16a−4=0 とおくと
15a2−16a+4=0
(3a−2)(5a−2)=0
a=32,52
af′(a)f(a)⋯− 520⋯+
520⋯+ 21+241⋯+
21+241⋯+ 320272⋯−
320272⋯− 1−−31
1−−31
g(21)=−5⋅81+8⋅41−4⋅21+32=241
g(32)=−5⋅278+8⋅94−4⋅32+32=272
g(1)=−5+8−4+32=−31
したがって,U は a=32 で最大値 272 をとる。
…ネノハヒフ
第2問 問題文
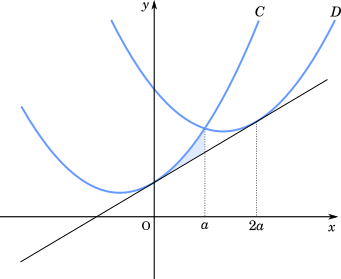
a > 0 とし, f(x)=x2−(4a−2)x+4a2+1 とおく。座標平面上で, 放物線 y=x2+2x+1 を C, 放物線 y=f(x) を D とする。また, ℓ を C と D の両方に接する直線とする。
(1) ℓ の方程式を求めよう。
ℓ と C は点 (t,t2+2t+1) において接するとすると, ℓ の方程式は
y=(アt+イ)x−t2+ウ⋯⋯①
である。また,ℓ と D は点 (s,f(s)) において接するとすると, ℓ の方程式は
y=(エs−オa+カ)x−s2+キa2+ク⋯⋯②
である。ここで, ① と ② は同じ直線を表しているので, t=ケ, s=コa が成り立つ。
したがって, ℓ の方程式は y=サx+シ である。
(2) 二つの放物線 C,D の交点の x 座標は ス である。
C と直線 ℓ, および直線 x=ス で囲まれた図形の面積を S とすると, S=ソaセ である。
(3) a≧21 とする。二つの放物線 C,D と直線 ℓ で囲まれた図形の中で 0≦x≦1 を満たす部分の面積 T は, a>タ のとき, a の値によらず
T=ツチ
であり, 21≦a≦タ のとき
T=−テa3+トa2−ナa+ヌニ
である。
(4) 次に, (2), (3) で定めた S,T に対して, U=2T−3S とおく。 a が 21≦a≦タ の範囲を動くとき, U は a=ノネ で最大値 ヒフハ をとる。
関連