【スマホで読む・わかりやすい】センター数学IIB2020本試【解説・正解・問題】

解答・解説

ア イ ウ 3 2 3　エ 3

オ カ キ ク 2 3 5 3　ケコ 12

サ シ 4 5　ス セ 3 5

ソ 3　タチ 11　ツテ 13

トナニ －36　ヌ ネノ 2 10

ハ ヒフ 3 －4　ヘ 7　ホ 5

(1)

加法定理を用いて

$\sqrt{3}\cos\bigg(\theta-\cfrac{\pi}{3}\bigg)=\sqrt{3}\bigg(\cos\theta\cos\cfrac{\pi}{3}+\sin\theta\sin\cfrac{\pi}{3}\bigg)$

$=\sqrt{3}\bigg(\cfrac{1}{2}\cos\theta+\cfrac{\sqrt{3}}{2}\sin\theta\bigg)$

$=\cfrac{\sqrt{3}}{2}\cos\theta+\cfrac{3}{2}\sin\theta$

…アイウ

よって

$\sin\theta\gt\cfrac{\sqrt{3}}{2}\cos\theta+\cfrac{3}{2}\sin\theta$

$\cfrac{1}{2}\sin\theta+\cfrac{\sqrt{3}}{2}\cos\theta\lt 0$

三角関数の合成を用いて

$\sin\bigg(\theta+\cfrac{\pi}{3}\bigg)\lt 0$

…ウ

よって

$\pi\lt\theta+\cfrac{\pi}{3}\lt2\pi$

$\cfrac{2}{3}\pi\lt\theta\lt\cfrac{5}{3}\pi$

…オカキク

(2)

$25x^2-35x+k=0$

解と係数の関係より

$\alpha+\beta=\cfrac{35}{25}=\cfrac{7}{5}$

$\sin\theta+\cos\theta=\cfrac{7}{5}$

$\alpha\beta=\cfrac{k}{25}$

$\sin\theta\cos\theta=\cfrac{k}{25}$

ここで，$\sin\theta+\cos\theta$ を 2 乗した上で，公式 $\sin^2 x+\cos^2 x=1$ を用いるとよい

$(\sin\theta+\cos\theta)^2=\cfrac{49}{25}$

$\sin^2\theta+2\sin\theta\cos\theta+\cos^2\theta=\cfrac{49}{25}$

$1+2\sin\theta\cos\theta=\cfrac{49}{25}$

$2\sin\theta\cos\theta=\cfrac{24}{25}$

$\sin\theta\cos\theta=\cfrac{12}{25}$

よって

$\cfrac{k}{25}=\cfrac{12}{25}$

$k=12$

…ケコ

$k$ の値を $25x^2-35x+k=0$ に代入して

$25x^2-35x+12=0$

$(5x-3)(5x-4)=0$

$x=\cfrac{3}{5},\cfrac{4}{5}$

$\theta$ が $\sin\theta\geqq\cos\theta$ であることに注意すると

$\sin\theta=\cfrac{4}{5},\cos\theta=\cfrac{3}{5}$

…サシスセ

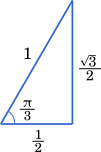
ここで，$\tan\theta$ を比べると

$\tan\theta=\cfrac{4}{3}\gt1$

$\tan\cfrac{\pi}{4}=1$ だから，$\theta\gt\cfrac{\pi}{4}$ であることが分かる。また $\tan\cfrac{\pi}{3}=\cfrac{\sqrt{3}}{1}=\sqrt{3}$ であるから，$\cfrac{4}{3}$ と $\sqrt{3}$ を比べると，それぞれ 2 乗して

$\cfrac{16}{9}\lt 3$

となる。よって，$\theta\lt\cfrac{\pi}{3}$ である。

したがって，$\cfrac{\pi}{4}\leqq\theta\lt\cfrac{\pi}{3}$

…ソ

〔2〕

$t^{\small\frac{1}{3}}-t^{-\small\frac{1}{3}}=-3$

両辺を 2 乗して

$(t^{\small\frac{1}{3}}-t^{-\small\frac{1}{3}})^2=9$

$t^{\small\frac{2}{3}}-2+t^{\small-\frac{2}{3}}=9$

$t^{\small\frac{2}{3}}+t^{\small-\frac{2}{3}}=11$

…タチ

次に $t^{\small\frac{1}{3}}+t^{\small-\frac{1}{3}}$
の両辺を 2 乗して

$(t^{\small\frac{1}{3}}+t^{\small-\frac{1}{3}})^2=t^{\small\frac{2}{3}}+2+t^{\small-{\frac{2}{3}}}$

$=11+2=13$

よって

$t^{\small\frac{1}{3}}+t^{\small-\frac{1}{3}}=\sqrt{13}$

…ツテ

また，$t^{\small\frac{1}{3}}-t^{\small-\frac{1}{3}}=-3$ の両辺を 3 乗して

$(t^{\small\frac{1}{3}}-t^{\small-\frac{1}{3}})^3=-27$

$t-3t^{\small\frac{2}{3}}\cdot t^{\small-\frac{1}{3}}+3t^{\small{\frac{1}{3}}}\cdot t^{\small{-\frac{2}{3}}}-t^{-1}=-27$

$t-t^{-1}-3(t^{\small\frac{1}{3}}-t^{\small-\frac{1}{3}})=-27$

$t-t^{-1}+9=-27$

$t-t^{-1}=-36$

…トナニ

(2)

② の左辺を変形すると

$\log_3(x\sqrt{y})=\log_3 x+\log_3\sqrt{y}$

$=\log_3 x+\log_3 y^{\small\frac{1}{2}}$

$=\log_3 x+\cfrac{1}{2}\log_3 y$

$=X+\cfrac{1}{2}Y$

よって ② は

$X+\cfrac{1}{2}Y\leqq5$

$2X+Y\leqq10\cdots\cdots$④

…ヌネノ

③ の左辺を変形すると

$\log_{81}\cfrac{y}{x^3}=\log_{81}y-\log_{81}x^3$

底の変換の公式 $\log_a b=\cfrac{\log_c b}{\log_c a}$ を用いて

$=\cfrac{\log_3 y}{\log_3 81}-\cfrac{\log_3 x^3}{\log_3 81}$

$=\cfrac{\log_3 y-3\log_3 x}{4}$

$=\cfrac{Y-3X}{4}$

よって ③ は

$\cfrac{Y-3X}{4}\leqq1$

$Y-3X\leqq4$

$3X-Y\geqq-4\cdots\cdots$⑤

…ハヒフ

次に $Y$ のとり得る最大の整数の値を求めると

④ を変形して

$Y\leqq-2X+10$

また， ⑤ を変形して

$Y\leqq3X+4$

これより

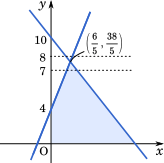
$\begin{cases}Y=-2X+10\\Y=3x+4\end{cases}$

として，その交点を求める。式を連立すると

$-2X+10=3X+4$

$5X=6$

$X=\cfrac{6}{5}$

これを式に代入して

$Y=-2\cdot\cfrac{6}{5}+10$

$=-\cfrac{12}{5}+10$

$=\cfrac{38}{5}$

グラフより $Y$ の取り得る最大の整数の値は $7$ であることが分かる。

…ヘ

さらに $Y=7$ を ④ に代入して

$2X+7\leqq10$

$2X\leqq3$

$X\leqq\cfrac{3}{2}$

$3X-7\geqq-4$

$3X\geqq3$

$X\geqq1$

よって $1\leqq X\leqq\cfrac{3}{2}$

$1\leqq\log_3 x\leqq\cfrac{3}{2}$

ここで $x$ の最大値を考えるために $\log_3 x=\cfrac{3}{2}$ とおくと

$x=3^{\small\frac{3}{2}}=\sqrt{3^3}=3\sqrt{3}$

$3\sqrt{3}$ の大きさを考えると

$\sqrt{3}\lt2$

$3\sqrt{3}\lt6$

よって $0\lt x\lt 6$

したがって $x$ のとり得る最大の整数の値は $5$

…ホ

第1問　問題文

〔1〕

(1) $0\leqq\theta\lt2\pi$ のとき

$\sin\theta\\gr\sqrt{3}\cos\bigg(\theta-\cfrac{\pi}{3}\bigg)\cdots\cdots$①

となる $\theta$ の値の範囲を求めよう。

加法定理を用いると

$\sqrt{3}\cos\bigg(\theta-\cfrac{\pi}{3}\bigg)=\cfrac{\sqrt{\boxed{\text{ア}}}}{\boxed{\text{イ}}}\cos\theta+\cfrac{\boxed{\text{ウ}}}{\boxed{\text{イ}}}\sin\theta$

である。よって, 三角関数の合成を用いると, ① は

$\sin\bigg(\theta+\cfrac{\pi}{\boxed{\text{エ}}}\bigg)\lt 0$

と変形できる。したがって, 求める範囲は

$\cfrac{\boxed{\text{オ}}}{\boxed{\text{カ}}}\pi\lt\theta\lt\cfrac{\boxed{\text{キ}}}{\boxed{\text{ク}}}\pi$

である。

(2) $0\leqq\theta\leqq\cfrac{\pi}{2}$ とし, $k$ を実数とする。$\sin\theta$ と $\cos\theta$ は $x$ の2次方程式 $25x^2-35x^2+k=0$ の解であるとする。このとき, 解と係数の関係により $\sin\theta+\cos\theta$ と $\sin\theta\cos\theta$ の値を考えれば, $k=\boxed{\text{ケコ}}$ であることがわかる。

さらに, $\theta$ が $\sin\theta\geqq\cos\theta$ を満たすとすると, $\sin\theta=\cfrac{\boxed{\text{サ}}}{\boxed{\text{シ}}}$, $\cos\theta=\cfrac{\boxed{\text{ス}}}{\boxed{\text{セ}}}$ である。このとき, $\theta$ は $\boxed{\text{ソ}}$ を満たす。$\boxed{\text{ソ}}$ に当てはまるものを, 次の ⓪~⑤ のうちから一つ選べ。

⓪ $0\leqq\theta\lt\cfrac{\pi}{12}$　① $\cfrac{\pi}{12}\leqq\theta\lt\cfrac{\pi}{6}$

② $\cfrac{\pi}{6}\leqq\theta\lt\cfrac{\pi}{4}$　③ $\cfrac{\pi}{4}\leqq\theta\lt\cfrac{\pi}{3}$

⓪ $\cfrac{\pi}{3}\leqq\theta\lt\cfrac{5}{12}\pi$　① $\cfrac{5}{12}\pi\leqq\theta\leqq\cfrac{\pi}{2}$

〔2〕

(1) $t$ は正の実数であり, $t^{\small\frac{1}{3}}-t^{\small-\frac{1}{3}}=-3$ を満たすとする。このとき

$t^{\small\frac{2}{3}}+t^{\small-\frac{2}{3}}=\boxed{\text{タチ}}$

である。さらに

$t^{\small\frac{1}{3}}+t^{\small-\frac{1}{3}}=\sqrt{\boxed{\text{ツテ}}}$, $t-t^{-1}=\boxed{\text{トナニ}}$

である。

(2) $x$, $y$ は正の実数とする。連立不等式

$\begin{cases}\log_3(x\sqrt{y})\leqq5\cdots\cdots\text{②}\\\log_{81}\cfrac{y}{x^3}\leqq1\cdots\cdots\text{③}\end{cases}$

について考える。

$X=\log_3 x$, $y=\log_3 y$ とおくと, ②は

$\boxed{\text{ヌ}}X+Y\leqq\boxed{\text{ネノ}}\cdots\cdots$④

と変形でき, ③ は

$\boxed{\text{ハ}}X-Y\geqq\boxed{\text{ヒフ}}\cdots\cdots$⑤

と変形できる。

$X$, $Y$ が $4$ と $5$ を満たすとき, $Y$ のとり得る最大の整数の値は $\boxed{\text{ヘ}}$ である。また, $x$, $y$ が ②, ③ と $\log_3 y=\boxed{\text{ヘ}}$ を同時に満たすとき, $x$ のとり得る最大の整数の値は、$\boxed{\text{ホ}}$ である。