【スマホで読む・わかりやすい】センター数学IIB2019追試【解説・正解・問題】

第2問　正解と解説

ア 0　イウ －3　エ,オ,カ 3, 3, 2
キ 0　クケ －3　コサ －1　シ 1
ス 3　セ 1　ソ タ 1 3
チ,ツ,テ 3, 1, 3　ト 2
ナ,ニ,ヌ 6, 2, 3
ネ ノ 1 3　ハ 3

(1)

$x=1$ で極値をとるので

$f'(1)=0$

・・・ア

$f(x)=px^3+qx$ より

$f'(x)=3px^2+q$

$f'(1)=3p+q=0$

$q=-3p$

・・・イ

よって $f(x)$ は

$f(x)=px^3-3px$

また

$f'(x)=3px^2-3p$

となる。以下，$f(x)$，$f'(x)$ の式はこれを用いて考えていく。

$x=s$ のとき接線の傾きは

$f'(s)=3ps^2-3p$

これが ($s$，$ps^3-3ps$) を通るので，接線は

$y-ps^3+3ps=(3ps^2-3p)(x-s)$

$y=(3ps^2-3p)x-(3ps^2-3p)s+ps^3-3ps$

$=(3ps^2-3p)x-3ps^3+3ps+ps^3-3ps$

$=(3ps^2-3p)x-2ps^3\cdots\cdots$①

・・・エオカ

接線の傾きを

$g(s)=3ps^2-2p$

とすると，条件 $p$ ＞ 0 より，$s=0$ のとき最小値 $-2p$ をとる。

・・・キクケ

(2)

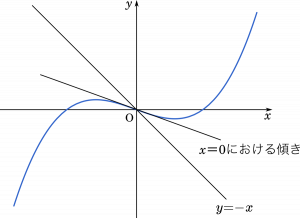
$x=0$ のときの接線の傾きは

$f'(0)=-3p$

条件 $p$ ＞ 0 より，接線は右下がりであり，$f(x)$ のグラフは上に示した形になる。

$-3p$ ≧ －1 のとき

$y=-x$ との共有点は 1 個。

・・・シ

また，直線 $y=-x$ を $y=-x+r$ として平行移動しても，共有点は 1 個である。このとき

$-3p$ ≧ －1

$p$ ≦ $\cfrac{1}{3}$

$-3p$ ＜ －1 のとき

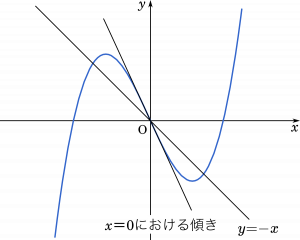
共有点は 3 個。

・・・ス

したがって，$C$ と直線 $\ell$ の共有点の個数が，$r$ の値によらず 1 個となるのは 0 ＜ $p$ ≦ $\cfrac{1}{3}$ のときである。

・・・セソタ

(3)

$p$ ＞ $\cfrac{1}{3}$ とすると

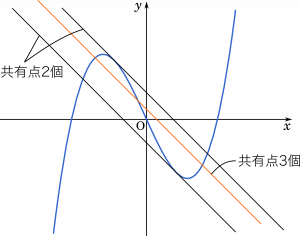
$f'(x)=3px^2-3p$ より，$(s,ps^3-3ps)$ における接線の傾きが －1 になるとき

$3ps^2-3p=-1$

$3ps^2=3p-1$

$s^2=\cfrac{3p-1}{3p}$

$s=\pm\sqrt{\cfrac{3p-1}{3p}}$

・・・チツテ

$\ell$ が接線のどちらかに一致するとき，$C$ と $\ell$ の共有点は 2 個。

・・・ト

このとき $\ell$ は傾き －1 で $(s,ps^3-3ps)$ を通るから，接線の式は

$y-ps^3+3ps=-(x-s)$

$y=-x+s+ps^3-3ps$

これが $y$ 軸を通るとき，(0, $r$) を通るから

$r=s+ps^3-3ps$

$=(1-3p+ps^2)s$

$=\Big(1-3p+p\cdot\cfrac{3p-1}{3p}\Big)\cdot\pm\sqrt{\cfrac{3p-1}{3p}}$

$=\cfrac{3-9p+3p-1}{3}\cdot\pm\sqrt{\cfrac{3p-1}{3p}}$

$=\cfrac{2-6p}{3}\cdot\pm\sqrt{\cfrac{3p-1}{3p}}$

ここから $|r|$ を求める。絶対値とは原点からの距離であることに注意すると，$\pm\sqrt{\cfrac{3p-1}{3p}}$ の絶対値は $\sqrt{\cfrac{3p-1}{3p}}$ であることが分かる。また，$\cfrac{2-6p}{3}$ の絶対値を考えると

$p$ ＞ $\cfrac{1}{3}$

$6p$ ＞ 2

$-6p$ ＜ －2

$2-6p$ ＜ 0

よって，$\Big|\cfrac{2-6p}{3}\Big|=\cfrac{6p-2}{3}$ だから

$|r|=\cfrac{6p-2}{3}\sqrt{\cfrac{3p-1}{3p}}$

・・・ナニヌ

(4)

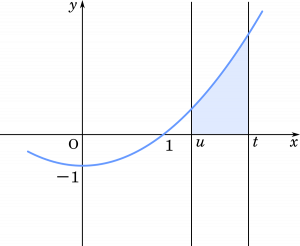
図形の面積と $f(t)$ は等しいから

$\displaystyle\int_u^t x^2-1\space dx=\Big[\cfrac{x^3}{3}-x\Big]_u^t$

$=\cfrac{t^3}{3}-t-\cfrac{u^3}{3}+u=pt^3-3pt$

両辺を比べると

$p=\cfrac{1}{3}$

・・・ネノ

$-\cfrac{u^3}{3}+u=0$

$\cfrac{u^3}{3}=u$

$\cfrac{u^2}{3}=1$

$u^2=3$

$u$ ≧ 1 より

$u=\sqrt{3}$

・・・ハ

問題文

$p$，$q$，$r$ を実数とし，$p$ ＞ 0 とする。関数 $f(x)=px^3+qx$ は $x=1$ で極値をとるとする。曲線 $y=f(x)$ を $C$，直線 $y=-x+r$ を $\ell$ とする。

(1) $f'(1)=\boxed{\text{ア}}$ であるから，$q=\boxed{\text{イウ}}\space p$ である。また，点($s$，$f(s)$)における曲線 $C$ の接線は

$y=(\boxed{\text{エ}}ps^2-\boxed{\text{オ}}\space p)x-\boxed{\text{カ}}\space ps^3\cdots\cdots$①

と表せる。よって，$C$ の接線の傾きは，$s=\boxed{\text{キ}}$ のとき最小値 $\boxed{\text{クケ}}\space p$ をとる。

(2) 曲線 $C$ と直線 $y=-x$ の共有点の個数は，$\boxed{\text{クケ}}\space p$ ≧ $\boxed{\text{コサ}}$ のとき $\boxed{\text{シ}}$ 個で，$\boxed{\text{クケ}}\space p$ ＜ $\boxed{\text{コサ}}$ のとき $\boxed{\text{ス}}$ 個となる。

$C$ と直線 $\ell$ の共有点の個数が，$r$ の値によらず $\boxed{\text{セ}}$ 個となるのは 0 ＜ $p$ ≦ $\cfrac{\boxed{\text{ソ}}}{\boxed{\text{タ}}}$ のときであり，$p$ ＞ $\cfrac{\boxed{\text{ソ}}}{\boxed{\text{タ}}}$ のときは $C$ と $\ell$ の共有点の個
数が，$r$ の値によって 1 個，2 個および 3 個の場合がある。

(3) p ＞ $\cfrac{\boxed{\text{ソ}}}{\boxed{\text{タ}}}$ とし，曲線 $C$ と直線 $\ell$ が 3 個の共有点をもつような $r$ の値の範囲を $p$ を用いて表そう。点($s$，$f(s)$)における $C$ の接線の傾きが －1 となる
のは $s=\pm\sqrt{\cfrac{\boxed{\text{チ}}\space p-\boxed{\text{ツ}}}{\boxed{\text{テ}}\space p}}$ のときである。したがって，傾きが －1 となる $C$ の接線は 2 本あり，$\ell$ がこれらの接線のどちらかに一致するとき，$C$ と $\ell$ の共有点は $\boxed{\text{ト}}$ 個となる。① を用いて，これら 2 本の接線と $y$ 軸との交点を求めれば，$C$ と $\ell$ が 3 個の共有点をもつような $r$ の絶対値の範囲は

$|r|$ ＜ $\cfrac{\boxed{\text{ナ}}\space p-\boxed{\text{ニ}}}{\boxed{\text{ヌ}}}\sqrt{\cfrac{\boxed{\text{チ}}\space p-\boxed{\text{ツ}}}{\boxed{\text{テ}}\space p}}$

であることがわかる。

(4) $u$ を 1 以上の実数とする。$t$ が $t$ ＞ $u$ の範囲を動くとき，曲線 $y=x^2-1$ と $x$ 軸および 2 直線 $x=u$，$x=t$ で囲まれた図形の面積が $f(t)$ とつねに等しいとする。このとき，$p=\cfrac{\boxed{\text{ネ}}}{\boxed{\text{ノ}}}$ であり，$u=\sqrt{\boxed{\text{ハ}}}$ となる。