【スマホで読む・わかりやすい】センター数学IIB2019追試【解説・正解・問題】

第1問　正解と解説

ア イ ウ 6 2 9　エ 0　オ カ 3 4
キク ケ －4 3　コ 5　サ,シ,ス 2, 6, 8
セ ソ 1 3　タ 1　チ 2　ツ 7
テ ト 3 1　ナ 2　ニ 0　ヌ 0
ネ 4　ノ 3　ハヒ 11

〔1〕(1)

円 $C$ の方程式は

$C:(x-3)^2+(y-1)^2=1$

$x^2-6x+9+y^2-2y+1=1$

$x^2+y^2-6x-2y+9=0$

・・・アイウ

〔1〕(2)

円の半径は 1 だから，円 $C$ と直線 $\ell$ が接するとき，円の中心 I と直線 $\ell$ の距離は 1 になる。

$\ell:y=ax$

移行して

$ax-y=0$

点と直線の距離の公式 $d=\cfrac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}$ より

$\cfrac{|a\cdot3-1\cdot1}{\sqrt{a^2+(-1)^2}}=1$

$|3a-1|=\sqrt{a^2+1}$

両辺を 2 乗して

$(3a-1)^2=a^2+1$

(左辺について，式を 2 乗したものは正の値となるので絶対値を外すことができる。)

$9a^2-6a+1=a^2+1$

$8a^2-6a=0$

$a^2-\cfrac{3}{4}a=0$

$a\Big(a-\cfrac{3}{4}\Big)=0$

$a=0$，$\cfrac{3}{4}$

・・・エオカ

$a=\cfrac{3}{4}$ のとき，直線 $\ell$ は

$\ell:y=\cfrac{3}{4}x$

$C$ と $\ell$ の接点を通り，$\ell$ に垂直な直線は円の中心 I を通る。直線の傾きを $m$ とすると

$\cfrac{3}{4}m=-1$ より $m=-\cfrac{4}{3}$

直線は (3，1) を通るので，式は

$y-1=-\cfrac{4}{3}(x-3)$

$y=-\cfrac{4}{3}x+4+1$

$=\cfrac{-4}{3}x+5$

・・・キクケコ

〔1〕(3)

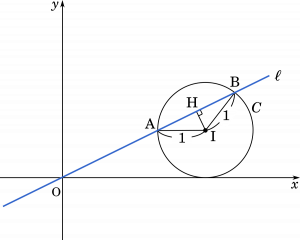
円の中心 I を通り直線 AB に垂直な直線と AB の交点を H とおく。IH の長さを求めると(1)より

IH ＝ $\cfrac{|3a-1|}{\sqrt{a^2+1}}$

三平方の定理より

$\text{AH}^2=1^2-\text{IH}^2$

$=1-\cfrac{(3a-1)^2}{a^2+1}$

$=\cfrac{a^2+1-9a^2+6a-1}{a^2+1}$

$=\cfrac{6a-8a^2}{a^2+1}$

AH ＝ $\sqrt{\cfrac{6a-8a^2}{a^2+1}}$

AB ＝ AH＋BH ＝ 2AH だから

AB ＝ $2\sqrt{\cfrac{6a-8a^2}{a^2+1}}$

・・・サシス

AB の長さが 2 のとき

$2\sqrt{\cfrac{6a-8a^2}{a^2+1}}=2$

$\sqrt{\cfrac{6a-8a^2}{a^2+1}}=1$

両辺を 2 乗して

$\cfrac{6a-8a^2}{a^2+1}=1$

$6a-8a^2=a^2+1$

$9a^2-6a+1=0$

$(3a-1)^2=0$

$a=\cfrac{1}{3}$

・・・セソ

〔2〕(1)

$2^0=1$ だから

$\log_21=0$

・・・タ

$2^1=2$ だから

$\log_22=1$

・・・チ

また $\log_2x=t$ とおくと

$2^t=x$

$x$ が 100 以下の自然数となるのは

$t=0,1,2,3,4,5,6$

のときである。したがって全部で 7 個。

・・・ツ

〔2〕(2)

$r=\log_23$ とおくと

$\log_254=\log_2(2\cdot3^3)$

$=\log_22+\log_23^3$

$=1+3\log_23$

$=3r+1$

・・・テト

また，$\log_25$ と $\cfrac{r+3}{2}$ の大きさをくらべると

$\cfrac{r+3}{2}=\cfrac{\log_23+\log_28}{\log_24}$

$=\cfrac{\log_2(3\cdot8)}{\log_24}$

底の変換公式の逆を用いて

$=\log_424$

また $\log_25$ は底の変換公式を用いて

$\log_25=\cfrac{\log_45}{\log_42}$

ここで $4^{\small{\frac{1}{2}}}=2$ だから，$\log_42=\cfrac{1}{2}$

$=\cfrac{\log_45}{\cfrac{1}{2}}=\cfrac{\log_45\times2}{\cfrac{1}{2}\times2}$

$=2\log_45=\log_45^2$

$=\log_425$

したがって

$\log_425$ ＞ $\log_424$

$\log_25$ ＞ $\cfrac{r+3}{2}$

・・・ナ

また，$\log_{\small\frac{1}{2}}\cfrac{1}{\sqrt{3}}$ と $r$ の大きさを比べると

底の変換公式を用いて

$\log_{\small\frac{1}{2}}\cfrac{1}{\sqrt{3}}=\cfrac{\log_2\cfrac{1}{\sqrt{3}}}{\log_2\cfrac{1}{2}}$

$=\cfrac{\log_21-\log_23^{\small{\frac{1}{2}}}}{\log_22^{-1}}$

$=\cfrac{-\cfrac{1}{2}\log_23}{-\log_22}$

$=\cfrac{1}{2}\log_23=\cfrac{1}{2}r$

したがって

$\cfrac{1}{2}r$ ＜ $r$

$\log_{\small\frac{1}{2}}\cfrac{1}{\sqrt{3}}$ ＜ $r$

・・・ニ

〔2〕(3)

たとえば，$k=3$ とすると，$3^0=1$，$3^1=3$ だから

0 ＜ $\log_32$ ＜ 1

が成り立つ。これは $k$ が 3 以上のときも同様だから，$n$ ≦ $\log_k2$ ＜ $n+1$ を満たす整数 $n$ は 0

・・・ヌ

$\cfrac{m}{10}$ ≦ $\log_k2$ は

$k^{\small{\frac{m}{10}}}$ ≦ 2

と書き直せる。両辺を 10 乗すると

$(k^{\small{\frac{m}{10}}})^{10}$ ≦ $2^{10}$

$k^m$ ≦ $2^{10}$

・・・ネ

$\log_72$ は上の不等式より 0 ≦ $\log_72$ ＜ 1 だから，一の位は 0 である。また $k^m$ ≦ $2^{10}$ において $k=7$ とすると

$7^m$ ≦ $2^{10}=1024$

$7^3=343$，$7^4=2401$ だから $m$ の最大は 3

よって $\cfrac{3}{10}$ ≦ $\log_72$ となるので，小数第一位の数字は 3

・・・ノ

$\log_k2$ の小数第一位の数字が 2 のとき

$k^2$ ≦ $2^{10}=(2^5)^2$

$k$ は正の数だから

$k$ ≦ 32

$\log_k2$ の小数第一位の数字が 3 のとき

$k^3$ ≦ $2^{10}=1024$

$10^3=1000$，$11^3=1331$ だから $k$ の最大は 10

つまり，$k$ が 11 以上 32 以下のとき，小数第一位の数字が 2 になることが分かる。したがって，最小のものは 11

・・・ハヒ

問題文

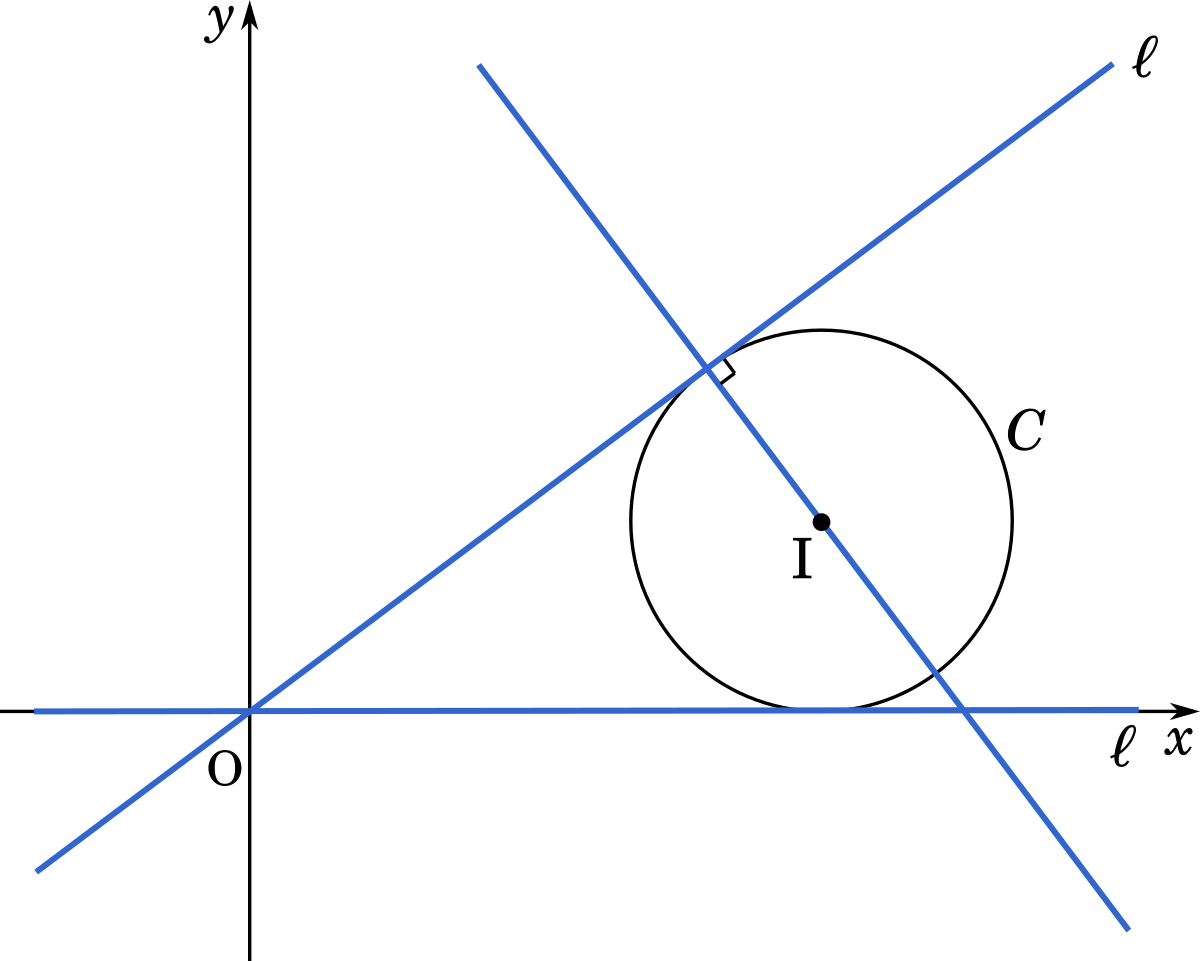
〔1〕$a$ を実数とする。座標平面上で，点(3，1)を中心とする半径 1 の円を $C$ とし，直線 $y=ax$ を $\ell$ とする。

(1) 円 $C$ の方程式は

$x^2+y^2-\boxed{\text{ア}}x-\boxed{\text{イ}}y+\boxed{\text{ウ}}=0$

である。

(2) 円 $C$ と直線 $\ell$ が接するのは

$a=\boxed{\text{エ}}$，$\cfrac{\boxed{\text{オ}}}{\boxed{\text{カ}}}$

のときである。

$a=\cfrac{\boxed{\text{オ}}}{\boxed{\text{カ}}}$ のとき，$C$ と $\ell$ の接点を通り，$\ell$ に垂直な直線の方程式は

$y=\cfrac{\boxed{\text{キク}}}{\boxed{\text{ケ}}}x+\boxed{\text{コ}}$

である。ただし，$\boxed{\text{キク}}$，$\boxed{\text{ケ}}$，$\boxed{\text{コ}}$ は，文字 $a$ を用いない形で答えること。

(3) 円 $C$ と直線 $\ell$ が異なる 2 点 A，Bで交わるとき，二つの交点を結ぶ線分 AB の長さは

$\boxed{\text{サ}}\sqrt{\cfrac{\boxed{\text{シ}}a-\boxed{\text{ス}}a^2}{a^2+1}}$

である。また，AB の長さが 2 となるのは

$a=\cfrac{\boxed{\text{セ}}}{\boxed{\text{ソ}}}$

のときである。

〔2〕

(1) $\log_2\boxed{\text{タ}}=0$，$\log_2\boxed{\text{チ}}=1$ である。また，100 以下の自然数 $x$ で $\log_2x$ が整数になるものは全部で $\boxed{\text{ツ}}$ 個ある。

(2) $r=\log_23$ とおく。このとき，$\log_254$ を $r$ を用いて表すと

$\log_254=\boxed{\text{テ}}r+\boxed{\text{ト}}$

となる。また，$\log_25$ と $\cfrac{r+3}{2}$，$\log_{\small{\frac{1}{2}}}\cfrac{1}{\sqrt{3}}$ と $r$ の大きさをそれぞれ比較すると

$\log_25$ $\boxed{\text{ナ}}$ $\cfrac{r+3}{2}$，$\log_{\small{\frac{1}{2}}}\cfrac{1}{\sqrt{3}}$ $\boxed{\text{ニ}}$ $r$

である。$\boxed{\text{ナ}}$，$\boxed{\text{ニ}}$ に当てはまるものを，次の⓪~②のうちから一つずつ選べ。ただし，同じものを選んでもよい。

⓪ ＜　① ＝　② ＞

(3) $k$ を 3 以上の整数とする。$\log_k2$ の値を調べよう。

$n$ ≦ $\log_k2$ ＜ $n+1$ を満たす整数 $n$ は $\boxed{\text{ヌ}}$ である。

また，整数 $m$ について，不等式 $\cfrac{m}{10}$ ≦ $\log_k2$ は，$\boxed{\text{ネ}}$ と書き直せることから，$\log_k2$ を小数で表したときの小数第1位の数字を求めることができる。$\boxed{\text{ネ}}$ に当てはまるものを，次の⓪~⑤のうちから一つ選べ。

⓪ $km$ ≦ 20　① $k^m$ ≦ 20

② $m^k$ ≦ 20　③ $km$ ≦ $2^{10}$

④ $k^m$ ≦ $2^{10}$　⑤ $m^k$ ≦ $2^{10}$

たとえば，$\log_72$ の小数第1位の数字は $\boxed{\text{ノ}}$ であり，$\log_k2$ の小数第1位の数字が 2 となる $k$ の値のうち最小のものは $\boxed{\text{ハヒ}}$ であることがわかる。