【スマホで読む・わかりやすい】センター数学IIB2019本試【解説・正解・問題】

第4問　解答・解説

アイ 90　ウ エ 5 2　オカ －1

キ 2　ク 2　ケコサ 120　シス 60

セ 2　ソ タ 2 2　チ ツ テ 3 3 2

ト 0　ナ,ニ ヌ 1，3 5

ネ ノ 5 5　ハ ヒ 1 6

フ 3　ヘ ホ 3 3

(1)

$\vec{a}\cdot\vec{c}=0$ だから ∠AOC＝90°

・・・アイ

公式 $s=\cfrac{1}{2}bc\sin A$ より

$S=\cfrac{1}{2}\cdot2\cdot\sqrt{5}=\cfrac{\sqrt{5}}{2}$

・・・ウエ

(2)

$\overrightarrow{\text{BA}}\cdot\overrightarrow{\text{BC}}=(\vec{a}-\vec{b})(\vec{c}-\vec{b})$

$=\vec{a}\cdot\vec{c}-\vec{a}\cdot\vec{b}-\vec{b}\cdot\vec{c}+|\vec{b}|^2$

＝0－1－3＋3＝－1

・・・オカ

$|\overrightarrow{\text{BA}}|^2=(\vec{a}-\vec{b})^2$

$=|\vec{a}|^2-2\vec{a}\cdot\vec{b}+|\vec{b}|^2$

＝1－2＋3＝2

よって

$|\overrightarrow{\text{BA}}|=\sqrt{2}$

・・・キ

また

$|\overrightarrow{\text{BC}}|^2=(\vec{c}-\vec{b})^2$

$=|\vec{c}|^2-2\vec{b}\cdot\vec{c}+|\vec{b}|^2$

＝5－6＋3＝2

よって

$|\overrightarrow{\text{BC}}|=\sqrt{2}$

・・・ク

また，$\overrightarrow{\text{BA}}\cdot\overrightarrow{\text{BC}}$ は

$\overrightarrow{\text{BA}}\cdot\overrightarrow{\text{BC}}=|\overrightarrow{\text{BA}}||\overrightarrow{\text{BC}}|\cos$∠ABC

と表すことができる。よって

$-1=\sqrt{2}\cdot\sqrt{2}\cos$∠ABC

$\cos$∠ABC＝$-\cfrac{1}{2}$

∠ABC ＝ 120°

・・・ケコサ

このことから

∠BAD ＝ ∠ADC ＝ 180°－120° ＝ 60°

・・・シス

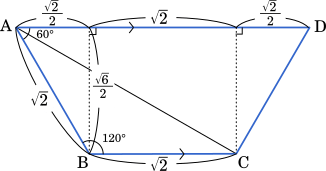
AD ＝ $\sqrt{2}+2\cdot\cfrac{\sqrt{2}}{2}=2\sqrt{2}$

よって，$\overrightarrow{\text{AD}}=2\overrightarrow{\text{BC}}$

・・・セ

また，$\overrightarrow{\text{OA}}$ は $\overrightarrow{\text{OD}}=\overrightarrow{\text{OA}}+\overrightarrow{\text{AD}}$ と表せるから

$\overrightarrow{\text{OD}}=\overrightarrow{\text{OA}}+2\overrightarrow{\text{BC}}$

$=\vec{a}+2(\vec{c}-\vec{b})$

$=\vec{a}-2\vec{b}+2\vec{c}$

・・・ソタ

四角形 ABCD は台形だから，面積を求めると

$\cfrac{1}{2}(\sqrt{2}+2\sqrt{2})\cdot\cfrac{\sqrt{6}}{2}$

$=\cfrac{3\sqrt{3}}{2}$

・・・チツテ

(3)

$\overrightarrow{\text{BH}}$ ⊥ $\vec{a}$ だから，$\overrightarrow{\text{OH}}$ ⊥ $\vec{a}$ が成り立つ。

$\overrightarrow{\text{OH}}\cdot\vec{a}=0$

・・・ト

また

$\overrightarrow{\text{OH}}=s\vec{a}+t\vec{b}$ とおくと

$\overrightarrow{\text{BH}}\cdot\vec{a}=(\overrightarrow{\text{OH}}-\overrightarrow{\text{OB}})\cdot\vec{a}$

$=\vec{a}\cdot\overrightarrow{\text{OH}}-\vec{a}\cdot\vec{b}$

$=s|\vec{a}|^2-t\vec{a}\cdot\vec{c}-\vec{a}\cdot\vec{b}$

$=s-1$

$\overrightarrow{\text{BH}}$ ⊥ $\vec{a}$ だから

$s-1=0$

$s=1$

・・・ナ

$\overrightarrow{\text{BH}}\cdot\vec{c}=(\overrightarrow{\text{OH}}-\overrightarrow{\text{OB}})\cdot\vec{c}$

$=s\vec{a}\cdot\vec{c}+t|\vec{c}|^2-\vec{b}\cdot\vec{c}$

$=5t-3$

$\overrightarrow{\text{BH}}$ ⊥ $\vec{c}$ だから

$5t-3=0$

$t=\cfrac{3}{5}$

・・・ニヌ

したがって $\overrightarrow{\text{OH}}=\vec{a}+\cfrac{3}{5}\vec{c}$

$|\overrightarrow{\text{BH}}|^2=(\overrightarrow{\text{OH}}-\overrightarrow{\text{OB}})^2$

$=(\vec{a}-\vec{b}+\cfrac{3}{5}c)^2$

$=\Big\{(\vec{a}-\vec{b})+\cfrac{3}{5}\vec{c}\Big\}^2$

$=(\vec{a}-\vec{b})^2+\cfrac{6}{5}(\vec{a}-\vec{b})\vec{c}+\cfrac{9}{25}|\vec{c}|^2$

$=|\vec{a}|^2-2\vec{a}\cdot\vec{b}+|\vec{b}|^2+\cfrac{6}{5}\vec{a}\cdot\vec{c}-\cfrac{6}{5}\vec{b}\cdot\vec{c}+\cfrac{9}{25}|\vec{c}|^2$

$=1^2-2\cdot1+(\sqrt{3})^2+\cfrac{6}{5}\cdot0-\cfrac{6}{5}\cdot3+\cfrac{9}{25}(\sqrt{5})^2$

$=1-2+3-\cfrac{18}{5}+\cfrac{9}{5}$

$=\cfrac{1}{5}$

よって

$|\overrightarrow{\text{BH}}|=\cfrac{\sqrt{5}}{5}$

・・・ネノ

$V=\cfrac{1}{3}\cdot\cfrac{\sqrt{5}}{2}\cdot\cfrac{\sqrt{5}}{5}=\cfrac{1}{6}$

・・・ハヒ

(4)

(3)の三角錐を今度は △ABC を底面とする三角錐とすると，四角錐 OABCD と高さが同じだから，体積の比は底面積の比に等しい。

△ABC の底辺を BC とし，△ADC の底辺を AD とすると，AD ＝ 2BC より，面積の比は 1：2 となる。よって，△ABC：四角形ABCD ＝ 1：3 だから，四角錐 OABCD の体積は $3V$ と表せる。

・・・フ

よって，体積は $\cfrac{1}{6}\cdot 3=\cfrac{1}{2}$

高さを $h$ とすると

$\cfrac{1}{3}\cdot\cfrac{3\sqrt{3}}{2}h=\cfrac{1}{2}$

$h=\cfrac{\sqrt{3}}{3}$

・・・ヘホ

第4問　問題文

四角形 ABCD を底面とする四角錐 OABCD を考える。四角形 ABCD は, 辺 AD と辺 BC が平行で, AB＝CD, ∠ABC＝∠BCD を満たすとする。さらに, $\overrightarrow{\text{OA}}=\vec{a}$, $\overrightarrow{\text{OB}}=\vec{b}$, $\overrightarrow{\text{OC}}=\vec{c}$ として

$|\vec{a}|=1$，$|\vec{b}|=\sqrt{3}$，$|\vec{c}|=\sqrt{5}$

$\vec{a}\cdot\vec{b}=1$，$\vec{b}\cdot\vec{c}=3$，$\vec{a}\cdot\vec{c}=0$

であるとする。

(1) ∠AOC＝$\boxed{\text{アイ}}$° により, 三角形 OAC の面積は $\cfrac{\sqrt{\boxed{\text{ウ}}}}{\boxed{\text{エ}}}$ である。

(2) $\overrightarrow{\text{BA}}\cdot\overrightarrow{\text{BC}}=\boxed{\text{オカ}}$，$|\overrightarrow{\text{BA}}|=\sqrt{\boxed{\text{キ}}}$，$|\overrightarrow{\text{BC}}|=\sqrt{\boxed{\text{ク}}}$ であるから, ∠ABC＝$\boxed{\text{ケコサ}}$° である。さらに, 辺 AD と辺 BC が平行であるから, ∠BAD＝∠ADC＝$\boxed{\text{シス}}$° である。よって，$\overrightarrow{\text{AD}}=\boxed{\text{セ}}\overrightarrow{\text{BC}}$ であり

$\overrightarrow{\text{AD}}=\vec{a}-\boxed{\text{ソ}}\vec{b}+\boxed{\text{タ}}\vec{c}$

と表される。また, 四角形 ABCD の面積は $\cfrac{\boxed{\text{チ}}\sqrt{\boxed{\text{ツ}}}}{\boxed{\text{テ}}}$ である。

(3) 三角形 OAC を底面とする三角錐 BOAC の体積 $V$ を求めよう。

3 点 O, A, C の定める平面 $\alpha$ 上に, 点 H を $\overrightarrow{\text{BH}}$⊥$\vec{a}$ と $\overrightarrow{\text{BH}}$⊥$\vec{c}$ が成り立つようにとる。$|\overrightarrow{\text{BH}}|$ は三角錐 BOAC の高さである。H は $\alpha$ 上の点であるから,実数 $s$, $t$ を用いて $\overrightarrow{\text{OH}}=s\vec{a}+t\vec{c}$ の形に表される。

$\overrightarrow{\text{BH}}\cdot\vec{a}=\boxed{\text{ト}}$，$\overrightarrow{\text{BH}}\cdot\vec{c}=\boxed{\text{ト}}$ により，$s=\boxed{\text{ナ}}$，$t=\cfrac{\boxed{\text{ニ}}}{\boxed{\text{ヌ}}}$ である。よって，$|\overrightarrow{\text{BH}}|=\cfrac{\sqrt{\boxed{\text{ネ}}}}{\boxed{\text{ノ}}}$ が得られる。したがって, (1)により, $V=\cfrac{\boxed{\text{ハ}}}{\boxed{\text{ヒ}}}$ であることがわかる。

(4) (3)の $V$ を用いると, 四角錐 OABCD の体積は $\boxed{\text{フ}}V$ と表せる。さらに, 四角形 ABCD を底面とする四角錐 OABCD の高さは $\cfrac{\sqrt{\boxed{\text{ヘ}}}}{\boxed{\text{ホ}}}$ である。