【スマホで読む・わかりやすい】センター数学IIB2019本試【解説・正解・問題】

第2問　解答・解説

ア 0　イ 0　ウエ －3　オ 1　カキ －2

クケ －2　コ 2　サ シ a 2　ス セ 3 3

ソタ 12　チ ツ テ 3 a a　ト ナ 3 1

ニ 2　ヌ b　ネ 2　ノハ ヒ 12 5

フ ヘホ 3 25

(1)

$f(x)$ が $x=-1$ で極値 2 をとるから $f'(-1)=2$ が成り立つ。

$f'(x)=3x^2+2px+q$

$f'(-1)=3-2p+q=0$

・・・ア

また，$f(-1)=-1+p-q=2$ だから，式どうしを連立して足すと

$2-p=2$

$p=0$

・・・イ

値を代入して

$3-2\cdot0+q=0$

$q=-3$

・・・ウエ

よって

$f(x)=x^3-3x$

増減を調べると

$f'(x)=3x^2-3$

ここで，$3x^2-3=0$ とおくと

$x^2-1=0$

$x^2=1$

$x=\pm1$

$\def\arraystretch{1.25}\begin{array}{c:c:c:c:c:c} x &\cdots&-1\cdots&1&\cdots\\\hline f'(x)&+&0&-&0&+\\\hline f(x)&\nearrow&&\searrow&-2&\nearrow\end{array}$

$f(1)=1-3=-2$

したがって，$f(x)$ は $x=1$ で最小値 －2 をとる。

・・・オカキ

(2)

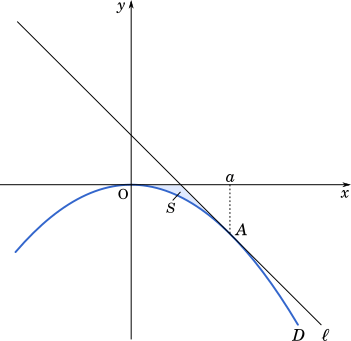
$D:y=-kx^2$

$y’=-2kx$

$x=a$ のとき，接線の傾きは $-2ka$

これが ($a$，$-ka^2$) を通るので

$\ell:y+ka^2=-2ka(x-a)$

$y=-2kax+ka^2\cdots\cdots$①

・・・クケコ

$x$ 軸との交点は

$0=-2kax+ka^2$

$2kax=ka^2$

$2x=a$

$x=\cfrac{a}{2}$

・・・サシ

次に，面積 $S$ を求める。

まず，$D$ と $x=a$ および $x$ 軸で囲まれた図形の面積を求める。図形は $x$ 軸より下にあるから，マイナスの符号をつけるとよい。

$\displaystyle -\int_0^a -kx^2\space dx$

$\displaystyle =k\int_0^a x^2\space dx$

$=k\Big[\cfrac{x^3}{3}\Big]_0^a$

$=\cfrac{k}{3}a^3$

・・・スセ

また，$\ell$ と $x=a$ および $x$ 軸で囲まれた三角形の面積は

$\cfrac{1}{2}\cdot\cfrac{a}{2}\cdot ka^2=\cfrac{k}{4}a^3$

よって

$S=\cfrac{k}{3}a^3-\cfrac{k}{4}a^3=\cfrac{k}{12}a^3$

・・・ソタ

(3)

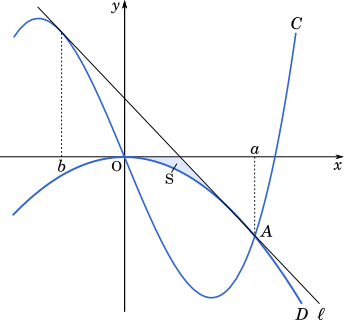
A($a$，$ka^2$) が $C:f(x)=x^3-3x$ 上にあるので

$-ka^2=a^3-3a$

$k=\cfrac{3}{a}-a$

・・・チツテ

$b$ を用いて $\ell$ の方程式を求めると

$f'(x)=3x^2-3$

$x=b$ のとき，傾きは $3b^2-3$

これが，($b$,$b^3-3b$) を通るので

$\ell:y-b^3+3b=(3b^2-3)(x-b)$

$y=(3b^2-3)x-(3b^2-3)b+b^3-3b$

$=3(b^2-1)x-3b^3+3b+b^3-3b$

$=3(b^2-2)x-2b^3\cdots\cdots$②

・・・トナニ

$g(x)=3(b^2-2)x-2b^3$ とおくと

$f(x)-g(x)=x^3-3x-3(b^2-1)x+2b^3$

$=x^3-3x-3b^2x+3x+2b^3$

$=x^3-3b^2x+2b^3$

$f(x)$ と $g(x)$ は $x=b$ で接するから

$x^3-3b^2x+2b^3=0$

が成り立つ。

これを因数分解するには，組立除法を用いるとよい。式の左辺は $x=b$ のとき 0 となるので

$\begin{aligned}1&&0&&-3b^2&&2b^3&&|\underline{b}\\&&b&&b^2&&-2b^3\\\hline 1&&b&&-2b^2&&0\end{aligned}$

$(x-b)(x^2+bx-2b^2)=0$

$(x-b)(x+2b)(2-b)=0$

$(x-b)^2(x+2b)=0$

よって

$f(x)-g(x)=(x-b)^2(x+2b)$

・・・ヌネ

また $f(x)$ と $g(x)$ は $x=a$ で交わるので，$(x-b)^2(x+2b)=0$ より，$a=-2b$ が成り立つ。

よって

$b=-\cfrac{a}{2}$

①と②で，直線の傾きどうしを比べると

$-2ka=3(b^2-1)$

$k$ と $b$ の値を代入して

$-2\Big(\cfrac{3}{a}-a\Big)a=3\Big\{\Big(-\cfrac{a}{2}\Big)^2-1\Big\}$

$-6+2a^2=\cfrac{3}{4}a^2-3$

$\cfrac{5}{4}a^2=3$

$a^2=\cfrac{12}{5}$

・・・ノハヒ

また，$S=\cfrac{k}{12}a^3$ より

$S=\cfrac{1}{12}\Big(\cfrac{3}{a}-a\Big)\cdot a^3$

$=\cfrac{a^2}{4}-\cfrac{a^4}{12}$

$=\cfrac{1}{4}\cdot\cfrac{12}{5}-\cfrac{1}{12}\cdot\Big(\cfrac{12}{5}\Big)^2$

$=\cfrac{3}{5}-\cfrac{12}{25}$

$=\cfrac{3}{25}$

・・・フヘホ

第2問　問題文

$p$，$q$ を実数とし, 関数 $f(x)=x^3+px^2+qx$ は $x=-1$ で極値 2 をとるとする。また, 座標平面上の曲線 $y=f(x)$ を $C$, 放物線 $y=-kx$ を $D$, 放物線 $D$ 上の点 $(a,-ka^2)$ を A とする。ただし, $k$ ＞ 0, $a$ ＞ 0 である。

(1) 関数 $f(x)$ が $x=-1$ で極値をとるので, $f'(-1)=\boxed{\text{ア}}$ である。これと $f(-1)=2$ より, $p=\boxed{\text{イ}}$，$q=\boxed{\text{ウエ}}$ である。よって, $f(x)$ は $x=\boxed{\text{オ}}$ で極小値 $\boxed{\text{カキ}}$ をとる。

(2) 点 A における放物線 $D$ の接線を $\ell$ とする。$D$ と $\ell$ および $x$ 軸で囲まれた図形の面積 $S$ を $a$ と $k$ を用いて表そう。

$\ell$ の方程式は

$y=\boxed{\text{クケ}}kax+ka^{\boxed{\text{コ}}}\cdots\cdots$①

と表せる。$\ell$ と $x$ 軸の交点の $x$ 座標は $\cfrac{\boxed{\text{サ}}}{\boxed{\text{シ}}}$ であり, $D$ と $x$ 軸および直線 $x=a$ で囲まれた図形の面積は $\cfrac{k}{\boxed{\text{ス}}}a^{\boxed{\text{セ}}}$ である。よって, $S=\cfrac{k}{\boxed{\text{ソタ}}}a^{\boxed{\text{セ}}}$ である。

(3) さらに, 点 A が曲線 $C$ 上にあり, かつ (2) の接線 $\ell$ が $C$ にも接するとする。このときの (2) の $S$ の値を求めよう。

A が $C$ 上にあるので, $k=\cfrac{\boxed{\text{チ}}}{\boxed{\text{ツ}}}-\boxed{\text{テ}}$ である。

$\ell$ と $C$ の接点の $x$ 座標を $b$ とすると, $\ell$ の方程式は $b$ を用いて

$y=\boxed{\text{ト}}(b^2-\boxed{\text{ナ}})x-\boxed{\text{ニ}}b^3\cdots\cdots$②

と表される。②の右辺を $g(x)$ とおくと

$f(x)-g(x)=(x-\boxed{\text{ヌ}})^2(x+\boxed{\text{ネ}}b)$ と因数分解されるので, $a=-\boxed{\text{ネ}}b$ となる。①と②の表す直線の傾きを比較することにより, $a^2=\cfrac{\boxed{\text{ノハ}}}{\boxed{\text{ヒ}}}$ である。

したがって, 求める $S$ の値は $\cfrac{\boxed{\text{フ}}}{\boxed{\text{ヘホ}}}$ である。