【スマホで読む・わかりやすい】センター数学IIB2018本試【解説・正解・問題】

第4問　解答・解説

ア 2　イ 2　ウ エ オ カ 3 4 1 4

キク ケ －3 4　コ サ,シ 1－a, a

スセ,ソ －a, 4　タチ －3　ツ,テ 9,6

トナ ニ ヌ 3a 2 2

(1)

$\overrightarrow{\text{AB}}=\overrightarrow{\text{FB}}-\overrightarrow{\text{FA}}=\vec{q}-\vec{p}$

・・・ア

$|\overrightarrow{\text{AB}}|^2=|\vec{p}|^2-2\vec{p}\cdot\vec{q}+|\vec{q}|^2\cdots\cdots$①

・・・イ

(2)

内分点の公式 $\dfrac{n\vec{a}+m\vec{b}}{m+n}$ より

$\overrightarrow{\text{FD}}=\dfrac{3\vec{p}+\vec{q}}{1+3}=\dfrac{3}{4}\vec{p}+\dfrac{1}{4}\vec{q}\cdots\cdots$②

・・・ウエオカ

(3)

$\overrightarrow{\text{FD}}=s\vec{r}$ より

$\dfrac{3}{4}\vec{p}+\dfrac{1}{4}\vec{q}=s\vec{r}$

$3\vec{p}+\vec{q}=4s\vec{r}$

$\vec{q}=-3\vec{p}+4s\vec{r}\cdots\cdots$③

・・・キクケ

E は BC の内分点だから

$\overrightarrow{\text{FE}}=(1-a)\vec{q}+a\vec{r}$

また，$\overrightarrow{\text{FE}}=t\vec{p}$ より

$(1-a)\vec{q}+a\vec{r}=t\vec{p}$

$(1-a)\vec{q}=t\vec{p}-a\vec{r}$

$\vec{q}=\dfrac{t}{1-a}\vec{p}-\dfrac{a}{1-a}\vec{r}\cdots\cdots$④

・・・コサシ

③と④を比べると

$-3=\dfrac{t}{1-a}$，$4s=\dfrac{-a}{1-a}$

$s=\dfrac{-a}{4(1-a)}$，$t=-3(1-a)$

・・・スセソタチ

(4)

①より

$|\overrightarrow{\text{AB}}|^2=1-2\vec{p}\cdot\vec{q}+|\vec{q}|^2$

また

$\overrightarrow{\text{BE}}=\overrightarrow{\text{FE}}-\overrightarrow{\text{FB}}$

$=t\vec{p}-\vec{q}$

$=-3(1-a)\vec{p}-\vec{q}$

$|\overrightarrow{\text{BE}}|^2=\{-3(1-a)\vec{p}-\vec{q}\}^2$

$=9(1-a)^2|\vec{p}|^2+6(1-a)\vec{p}\cdot\vec{q}+|\vec{q}|^2$

$=9(1-a)^2+6(1-a)\vec{p}\cdot\vec{q}+|\vec{q}|^2$

・・・ツテ

$|\overrightarrow{\text{AB}}|^2=|\overrightarrow{\text{BE}}|^2$ より

$1-2\vec{p}\cdot\vec{q}+|\vec{q}|^2=9(1-a)^2+6(1-a)\vec{p}\cdot\vec{q}+|\vec{q}|^2$

$6(1-a)\vec{p}\cdot\vec{q}+2\vec{p}\cdot\vec{q}=1-9(1-a)^2$

$\{6(1-a)+2\}\vec{p}\cdot\vec{q}=1-9(1-2a+a^2)$

$(6-6a+2)\vec{p}\cdot\vec{q}=1-9+18a-9a^2$

$(8-6a)\vec{p}\cdot\vec{q}=-9a^2+18a-8$

$(6a-8)\vec{p}\cdot\vec{q}=9a^2-18a+8$

$2(3a-4)\vec{p}\cdot\vec{q}=(3a-2)(3a-4)$

$2\vec{p}\cdot\vec{q}=3a-2$

$\vec{p}\cdot\vec{q}=\dfrac{3a-2}{2}$

・・・トナニヌ

第４問　問題文

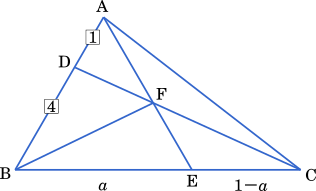
$a$ を 0 ＜ $a$ ＜ 1 を満たす定数とする。三角形 ABC を考え，辺 AB を 1：3 に内分する点を D，辺 BC を $a：(1-a)$ に内分する点を E，直線 AE と直線 CD
の交点を F とする。$\overrightarrow{\text{FA}}$ ＝ $\vec{p}$，$\overrightarrow{\text{FB}}$ ＝ $\vec{q}$，$\overrightarrow{\text{FC}}$ ＝ $\vec{r}$ とおく。

(1) $\overrightarrow{\text{AB}}$ ＝ $\boxed{\text{ア}}$ であり

$|\overrightarrow{\text{AB}}|^2=|\vec{p}|^2-\boxed{\text{イ}}\space\vec{p}\cdot\vec{q}+|\vec{q}|^2\cdots\cdots$①

である。ただし，$\boxed{\text{ア}}$ については，当てはまるものを，次の⓪～③のうちから一つ選べ。

⓪ $\vec{p}+\vec{q}$　① $\vec{p}-\vec{q}$

② $\vec{q}-\vec{p}$　③ $-\vec{p}-\vec{q}$

(2) $\overrightarrow{\text{FD}}$ を $\vec{p}$ と $\vec{q}$ を用いて表すと

$\overrightarrow{\text{FD}}$ ＝ $\cfrac{\boxed{\text{ウ}}}{\boxed{\text{エ}}}\vec{p}+\cfrac{\boxed{\text{オ}}}{\boxed{\text{カ}}}\vec{q}\cdots\cdots$②

である。

(3) $s$，$t$ をそれぞれ $\overrightarrow{\text{FD}}$ ＝ $s\vec{r}$，$\overrightarrow{\text{FE}}$ ＝ $t\vec{p}$ となる実数とする。$s$ と $t$ を $a$ を用いて表そう。

$\overrightarrow{\text{FD}}$ ＝ $s\vec{r}$ であるから，②により

$\vec{q}$ ＝ $\boxed{\text{キク}}\vec{p}+\boxed{\text{ケ}}s\vec{r}\cdots\cdots$③

である。また，$\overrightarrow{\text{FE}}$ ＝ $t\vec{p}$ であるから

$\vec{q}$ ＝ $\cfrac{t}{\boxed{\text{コ}}-\boxed{\text{サ}}}\vec{p}-\cfrac{\boxed{\text{シ}}}{\boxed{\text{コ}}-\boxed{\text{サ}}}\vec{r}\cdots\cdots$④

である。③と④により

$s$ ＝ $\cfrac{\boxed{\text{スセ}}}{\boxed{\text{ソ}}(\boxed{\text{コ}}-\boxed{\text{サ}})}$，$t$ ＝ $\boxed{\text{タチ}}(\boxed{\text{コ}}-\boxed{\text{サ}})$

である。

(4) $|\overrightarrow{\text{AB}}|$＝$|\overrightarrow{\text{BE}}|$ とする。$|\vec{p}|$ ＝ 1 のとき，$\vec{p}$ と $\vec{q}$ の内積を $a$ を用いて表そう。

①により

$|\overrightarrow{\text{AB}}|^2$ ＝ $1-\boxed{\text{イ}}\vec{p}\cdot\vec{q}+|\vec{q}|^2$

である。また

$|\overrightarrow{\text{BE}}|^2$ ＝ $\boxed{\text{ツ}}(\boxed{\text{コ}}-\boxed{\text{サ}})^2+\boxed{\text{テ}}(\boxed{\text{コ}}-\boxed{\text{サ}})\vec{p}\cdot\vec{q}+|\vec{q}|^2$

である。したがって

$\vec{p}\cdot\vec{q}=\cfrac{\boxed{\text{トナ}}-\boxed{\text{ニ}}}{\boxed{\text{ヌ}}}$

である。