【スマホで読む・わかりやすい】センター数学IIB2018本試【解説・正解・問題】

第1問　解答・解説

ア 2　イ ウ 4 5　エオカ 345　キ 6

ク 3　ケ コ 3 2　サシ スセ 29 30

ソ 2　タ 3　チ ツ 1 2　テ 0

ト ナ 3 9　ニ 2　ヌ ネ 3 4

ノ ハヒ 4 27

〔1〕

(1)

1 ラジアンとは半径が 1，弧の長さが 1 の扇形の中心角の大きさのことである。

・・・ア

(2)

144°を弧度で表すと，360°＝2π だから

$2\pi\times\cfrac{144}{360}=\cfrac{4}{5}\pi$

・・・イウ

$\cfrac{23}{12}\pi=x\degree$ とすると

$2\pi\times\cfrac{x}{360}=\cfrac{23}{12}\pi$

$\cfrac{\pi}{180}=\cfrac{23}{12}$

$x=\cfrac{23}{12}\cdot180=345\degree$

・・・エオカ

(3)

$x=\theta+\cfrac{\pi}{5}$ とおくと

$\theta+\cfrac{\pi}{30}=\theta+\cfrac{6-5}{30}$

$=\theta+\cfrac{1}{5}\pi-\cfrac{1}{6}\pi$

したがって，①は

$2\sin x-2\cos\Big(x-\cfrac{\pi}{6}\Big)=1$

・・・キ

加法定理を用いて

$2\sin x-2\Big(\cos x\cos\cfrac{\pi}{6}+\sin x\sin\cfrac{\pi}{6}\Big)=1$

$2\sin x-2\Big(\cos x\cdot\cfrac{\sqrt{3}}{2}+\sin x\cdot\cfrac{1}{2}\Big)=1$

$2\sin x-\sqrt{3}\cos x-\sin x=1$

$\sin x-\sqrt{3}\cos x=1$

・・・ク

三角関数の合成 $a\sin x+b\cos x=r\sin(x+\alpha)$ を用いて

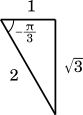
$2\sin\Big(x-\cfrac{\pi}{3}\Big)=1$

$\sin\Big(x-\cfrac{\pi}{3}\Big)=\cfrac{1}{2}$

・・・ケコ

$\cfrac{\pi}{2}$ ≦ $\theta$ ≦ $\pi$ より

$x-\cfrac{\pi}{3}=\cfrac{5}{6}\pi$

$x=\cfrac{7}{6}\pi$

$x=\theta+\cfrac{\pi}{5}$ より

$\cfrac{7}{6}\pi=\theta+\cfrac{\pi}{5}$

$\theta=\cfrac{29}{30}\pi$

・・・サシスセ

〔2〕

3 と底として②の両辺の対数をとり，$t=\log_3 x$ とおくと

$\log_3 x^t$ ≧ $\log_3\Big(\cfrac{x}{c}\Big)^3$

$t\log_3 x$ ≧ $3\log_3\Big(\cfrac{x}{c}\Big)$

$t\log_3 x$ ≧ $3\log_3 x-3\log_3 c$

$t^2$ ≧ $3t-3\log_3 c$

$t^2-3t+3\log_3 c$ ≧ 0 $\cdots\cdots$③

・・・ソタ

次に，$c=\sqrt[3]{9}=9^{\small{\frac{1}{3}}}$

③は

$t^2-3t+3\log_3 9^{\small{\frac{1}{3}}}$ ≧ 0

$t^2-3t+\cfrac{1}{3}\cdot3\log_3 9$ ≧ 0

$t^2-3t+2$ ≧ 0

$(t-1)(t-2)$ ≧ 0

$t$ ≦ 1，$t$ ≧ 2

・・・チツ

よって，$\log_3 x$ ≦ 1，$\log_3 x$ ≧ 2

ここで，$\log_3 x=1$ のとき，$x=3$ だから

0 ＜ $x$ ≦ 3

また，$\log_3 x=2$ のとき，$x=9$ だから

$x$ ≧ 9

・・・テトナ

次に，$x$ が $x$ ＞ 0 の範囲を動くとき，$t$ の取り得る値の範囲は実数全体である。

・・・ニ

このとき，横の軸を $t$ として③をグラフで表すと，グラフは $t$ 軸と交わることはない。つまり，$t^2-3t+3\log_3 c=0$ は実数解を持たないか 1 つ持つから，判別式を求めると

$D=9-4\cdot3\log_3c$ ≦ 0

9 ≦ $4\cdot3\log_3c$

$\log_3 c$ ≧ $\cfrac{3}{4}$

・・・ヌネ

ここで，$\log_3 c=\cfrac{3}{4}$ のとき，$3^{\small{\frac{3}{4}}}=c$ だから

$c$ ≧ $3^{\small\frac{3}{4}}$

$c$ ≧ $27^{\small{\frac{1}{4}}}$

$c$ ≧ $\sqrt[4]{27}$

・・・ノハヒ

第１問　問題文

〔1〕

(1) 1 ラジアンとは，$\boxed{\text{ア}}$ のことである。$\boxed{\text{ア}}$ に当てはまるものを，次の⓪～③のうちから一つ選べ。

⓪ 半径が 1，面積が 1 の扇形の中心角の大きさ

① 半径が π，面積が 1 の扇形の中心角の大きさ

② 半径が 1，弧の長さが 1 の扇形の中心角の大きさ

③ 半径が π，弧の長さが 1 の扇形の中心角の大きさ

(2) 144°を弧度で表すと $\cfrac{\boxed{\text{イ}}}{\boxed{\text{ウ}}}$ π ラジアンである。また，$\cfrac{23}{12}$ π ラジアンを度で表すと $\boxed{\text{エオカ}}$°である。

(3) $\cfrac{\pi}{2}$ ≦ $\theta$ ≦ π の範囲で

$2\sin\Big(\theta+\cfrac{\pi}{5}\Big)-2\cos\Big(\theta+\cfrac{\pi}{30}\Big)=1\cdots\cdots$①

を満たす $\theta$ の値を求めよう。

$x＝\theta+\cfrac{\pi}{5}$ とおくと，① は

$2\sin x-2\cos\Big(x-\cfrac{\pi}{\boxed{\text{キ}}}\Big)-1$

と表せる。加法定理を用いると，この式は

$\sin x-\sqrt{\boxed{\text{ク}}}\cos x=1$

となる。さらに，三角関数の合成を用いると

$\sin\Big(x-\cfrac{\pi}{\boxed{\text{ケ}}}\Big)=\cfrac{1}{\boxed{\text{コ}}}$

と変形できる。$x=\theta+\cfrac{\pi}{5}$，$\cfrac{\pi}{2}$≦ $\theta$ ≦ π だから，$\theta$＝$\cfrac{\boxed{\text{サシ}}}{\boxed{\text{スセ}}}$ π である。

〔2〕$c$ を正の定数として，不等式

$x^{\small{log_3 x}}$ ≧ $\Big(\cfrac{x}{c}\Big)^3\cdots\cdots$②

を考える。

3 を底とする②の両辺の対数をとり，$t$＝$\log_3 x$ とおくと

$t^{\boxed{\text{ソ}}}-\boxed{\text{タ}}t+\boxed{\text{タ}}\log_3 c$ ≧ 0 $\cdots\cdots$③

となる。ただし，対数 $log_a b$ に対し，$a$ を底といい，$b$ を真数という。

$c$＝$\sqrt[3]{9}$ のとき，②を満たす $x$ の値の範囲を求めよう。③により

$t$ ≦ $\boxed{\text{チ}}$，$t$ ≧ $\boxed{\text{ツ}}$

である。さらに，真数の条件を考えて

$\boxed{\text{テ}}$ ＜ $x$ ≦ $\boxed{\text{ト}}$， $x$ ≧ $\boxed{\text{ナ}}$

となる。

次に，②が $x$ ＞ $\boxed{\text{テ}}$ の範囲でつねに成り立つような $c$ の値の範囲を求めよう。

$x$ が $x$ ＞ $\boxed{\text{テ}}$ の範囲を動くとき，$t$ のとり得る値の範囲は $\boxed{\text{ニ}}$ である。$\boxed{\text{ニ}}$ に当てはまるものを，次の⓪～③のうちから一つ選べ。

⓪ 正の実数全体　① 負の実数全体

② 実数全体　③ 1 以外の実数全体

この範囲の $t$ に対して，③がつねに成り立つための必要十分条件は，$\log_3 c$ ≧ $\cfrac{\boxed{\text{ヌ}}}{\boxed{\text{ネ}}}$ である。すなわち，$c$ ≧ $\sqrt[\boxed{\text{ノ}}]{\boxed{\text{ハヒ}}}$ である。