【スマホで読む・わかりやすい】センター数学IIB2017追試【解説・正解・問題】
第4問 解答・解説
ア 8 イ 0 ウ 2 エ 2 オカ 60
キ 1 ク,ケ,コ 2,1,1 サシ スセ 13 18
ソ タ チ ツ 2 2 3 2
テ ト ナ ニヌ 1 9 1 12
ネ ノハ 1 18
$\overrightarrow{\text{DA}}=(2-x,-y,-z)$
$\overrightarrow{\text{DB}}=(1-x,1-y,-z)$
$\overrightarrow{\text{DC}}=(1-x,-y,1-z)$
となるので
$\overrightarrow{\text{DA}}\cdot\overrightarrow{\text{DB}}-\overrightarrow{\text{DB}}\cdot\overrightarrow{\text{DC}}$
$=(2-x)(1-x)+(-y)(1-y)+(-z)^2-(1-x)^2-(1-y)(-y)-(-z)(1-z)$
$=2-2x-x+x^2-y+y^2+z^2-1+2x-x^2+y-y^2+z-z^2$
$=z-x+1\cdots\cdots$①
・・・ア
$\overrightarrow{\text{DB}}\cdot\overrightarrow{\text{DC}}-\overrightarrow{\text{DC}}\cdot\overrightarrow{\text{DA}}$
$=(1-x)^2+(1-y)(-y)+(-z)(1-z)-(1-x)(2-x)-(-y)^2-(1-z)(-z)$
$=1-2x+x^2-y+y^2-z+z^2-2+x+2x-x^2-y^2+z-z^2$
$=x-y-1\cdots\cdots$②
・・・イ
(2)
三平方の定理より
AB=$\sqrt{(1-2)^2+(1-0)^2+(0-0)^2}$
=$\sqrt{2}$
・・・ウ
正四面体のすべての辺の長さは等しいから,
$\overrightarrow{\text{DA}}$,$\overrightarrow{\text{DB}}$,$\overrightarrow{\text{DC}}$ の大きさは,いずれも $\sqrt{2}$
・・・エ
また,すべての面は正三角形だから,どの二つのベクトルのなす角も 60°
・・・オカ
内積を求めると
$\overrightarrow{\text{DA}}\cdot\overrightarrow{\text{DB}}=\overrightarrow{\text{DB}}\cdot\overrightarrow{\text{DC}}=\overrightarrow{\text{DC}}\cdot\overrightarrow{\text{DA}}$
$=\sqrt{2}\cdot\sqrt{2}\cos60\degree$
$=2\cdot\cfrac{1}{2}=1$
・・・キ
次に,$(x,y,z)$ を求めるには,連立方程式を作るとよい。
①より
$\overrightarrow{\text{DA}}\cdot\overrightarrow{\text{DB}}-\overrightarrow{\text{DB}}\cdot\overrightarrow{\text{DC}}=1-1=0$
$z-x+1=0$
同様に,②より
$x-y-1=0$
式を足すと
$z-y=0$
$y=z$
これを用いて
$\overrightarrow{\text{DA}}=(2-x,-y,-y)$
$\overrightarrow{\text{DB}}=(1-x,1-y,-y)$
$\overrightarrow{\text{DC}}=(1-x,-y,1-y)$
と書き換えることができる。ここから,$x$ と $y$ の関係を表す式を作るために,辺の長さが $\sqrt{2}$ であることを利用するとよい。
$|\overrightarrow{\text{DA}}|^2=2$ より
$(2-x)^2+(-y)^2+(-y)^2=2$
$4-4x+x^2+2y^2=2$
$x^2+2y^2-4x+2=0$
$|\overrightarrow{\text{DB}}|^2=2$ より
$(1-x)^2+(1-y)^2+(-y)^2=2$
$1-2x+x^2+1-2y+y^2+y^2=2$
$x^2+2y^2-2x-2y=0$
2つの式を連立して引き算すると
$-2x+2y+2=0$
$x-y-1=0$
$y=x-1$
これを $x^2+2y^2-4x+2=0$ に代入すると
$x^2+2(x-1)^2-4x+2=0$
$x^2+2x^2-4x+2-4x+2=0$
$3x^2-8x+4=0$
$(x-2)(3x-2)=0$
$x=2$,$\cfrac{2}{3}$
$x$ > 1 より,$x$=2
よって,$y$=2-1=1,$z$=1
$(x,y,z)=(2,1,1)$
・・・クケコ
(3)
$\overrightarrow{\text{PQ}}=\overrightarrow{\text{DQ}}-\overrightarrow{\text{DP}}$
$=\cfrac{1}{3}\overrightarrow{\text{DA}}-\cfrac{1}{2}(\overrightarrow{\text{DA}}+\overrightarrow{\text{DB}})$
$=-\cfrac{1}{6}\overrightarrow{\text{DA}}-\cfrac{1}{2}\overrightarrow{\text{DB}}$
ここで,$(x,y,z)=(2,1,1)$ より
$\overrightarrow{\text{DA}}=(2-2,-1,-1)=(0,-1,-1)$
$\overrightarrow{\text{DB}}=(1-2,1-1,-1)=(-1,0,-1)$
$\overrightarrow{\text{DC}}=(1-2,-1,1-1)=(-1,-1,0)$
よって
$\overrightarrow{\text{PQ}}=-\cfrac{1}{6}(0,-1,-1)-\cfrac{1}{2}(-1,0,-1)$
$=(\cfrac{\space1\space}{2},\cfrac{\space1\space}{6},\cfrac{\space2\space}{3})$
$|\overrightarrow{\text{PQ}}|^2=\Big(\cfrac{1}{2}\Big)^2+\Big(\cfrac{1}{6}\Big)^2+\Big(\cfrac{2}{3}\Big)^2$
$=\cfrac{1}{4}+\cfrac{1}{36}+\cfrac{4}{9}=\cfrac{13}{18}$
・・・サシスセ
また
$\overrightarrow{\text{PR}}=\overrightarrow{\text{DR}}-\overrightarrow{\text{DP}}$
$=t\overrightarrow{\text{DC}}-\cfrac{1}{2}(\overrightarrow{\text{DA}}+\overrightarrow{\text{DB}})$
$=t(-1,-1,0)-\cfrac{1}{2}(0,-1,-1)-\cfrac{1}{2}(-1,0,-1)$
$=\Big(-t+\cfrac{1}{2},-t+\cfrac{1}{2},1\Big)$
$|\overrightarrow{\text{PR}}|^2=\Big(-t+\cfrac{1}{2}\Big)^2+\Big(-t+\cfrac{1}{2}\Big)^2+1$
$=t^2-t+\cfrac{1}{4}+t^2-t+\cfrac{1}{4}+1$
$=2t^2-2t+\cfrac{3}{2}$
・・・ソタチツ
さらに,$4S^2$ を求める。
$|\overrightarrow{\text{PQ}}||\overrightarrow{\text{PR}}|\cos\theta=\overrightarrow{\text{PQ}}\cdot\overrightarrow{\text{PR}}$
$=\cfrac{1}{2}\Big(-t+\cfrac{1}{2}\Big)+\cfrac{1}{6}\Big(-t+\cfrac{1}{2}\Big)+\cfrac{2}{3}\cdot1$
$=-\cfrac{t}{2}+\cfrac{1}{4}+\cfrac{1}{12}+\cfrac{2}{3}$
$=-\cfrac{2}{3}t+1$
よって
$4S^2=\cfrac{13}{18}\Big(2t^2-2t+\cfrac{3}{2}\Big)-(-\cfrac{3}{2}t+1\Big)^2$
$=\cfrac{13}{9}t^2-\cfrac{13}{9}t+\cfrac{13}{12}-\cfrac{4}{9}t^2+\cfrac{4}{3}t-1$
$=t^2-\cfrac{1}{9}t+\cfrac{1}{12}$
・・・テトナニヌ
式を平方完成すると
$=\Big(t-\cfrac{1}{18}\Big)^2-\cfrac{1}{18^2}+\cfrac{1}{12}$
よって,$S$ は $t=\cfrac{1}{18}$ のとき最小になる。
・・・ネノハ
第4問 問題文
座標空間において 4 点 A$(2,0,0)$, B$(1,1,0)$, C$(1,0,1)$, D$(x,y,z)$ を考える。
(1) 三つのベクトル $\overrightarrow{\text{DA}}$, $\overrightarrow{\text{DB}}$, $\overrightarrow{\text{DC}}$ について
$\overrightarrow{\text{DA}}\cdot\overrightarrow{\text{DB}}-\overrightarrow{\text{DB}}\cdot\overrightarrow{\text{DC}}=\boxed{\text{ア}}\cdots\cdots$①
$\overrightarrow{\text{DB}}\cdot\overrightarrow{\text{DC}}-\overrightarrow{\text{DC}}\cdot\overrightarrow{\text{DA}}=\boxed{\text{イ}}\cdots\cdots$②
である。$\boxed{\text{ア}}$, $\boxed{\text{イ}}$ に当てはまるものを, 次の⓪~⑧のうちから一つ ずつ選べ。ただし, 同じものを選んでもよい。
⓪ $x-y-1$ ① $y-z-1$ ② $z-x-1$
③ $x-y$ ④ $y-z$ ⑤ $z-x$
⑥ $z-y+1$ ⑦ $y-z+1$ ⑧ $z-x+1$
(2) AB = BC = CA = $\boxed{\text{ウ}}$ により, 三角形 ABC は正三角形である。以下, 4点 A, B, C, D が, 正四面体の四つの頂点になるとする。このときの $x, y, z$ の値を求めよう。ただし, $x\gt1$ とする。
ベクトル $\overrightarrow{\text{DA}}$, $\overrightarrow{\text{DB}}$, $\overrightarrow{\text{DC}}$ の大きさは, いずれも $\sqrt{\boxed{\text{エ}}}$ であり, どの二つのベクトルのなす角も $\boxed{\text{オカ}}\degree$ である。よって, $\overrightarrow{\text{DA}}\cdot\overrightarrow{\text{DB}}=\overrightarrow{\text{DB}}\cdot\overrightarrow{\text{DC}}=\overrightarrow{\text{DC}}\cdot\overrightarrow{\text{DA}}=\boxed{\text{キ}}$ となる。このことと①, ②および$|\overrightarrow{\text{DA}}|=|\overrightarrow{\text{DB}}|=|\overrightarrow{\text{DC}}|=\sqrt{\boxed{\text{エ}}}$ により, $(x, y, z)=(\boxed{\text{ク}},\boxed{\text{ケ}},\boxed{\text{コ}})$ となる。
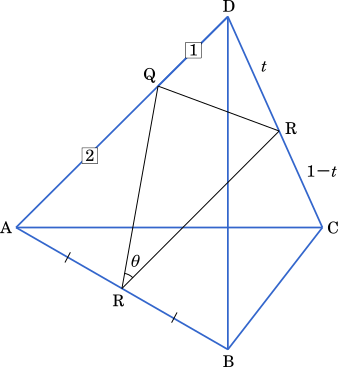
(3) $(x,y,z)=(\boxed{\text{ク}},\boxed{\text{ケ}},\boxed{\text{コ}})$ のときを考える。線分 AB の中点をP, 線分 DA を 1 : 2 に内分する点を Q, 線分 DC を $t : (1 – t)$ $(0\lt t\lt 1)$ に内分する点を R とする。三角形 PQR の面積 $S$ が最小になるときの $t$ の値を求めよう。
$|\overrightarrow{\text{PQ}}|^2=\cfrac{\boxed{\text{サシ}}}{\boxed{\text{スセ}}}$, $|\overrightarrow{\text{PR}}|^2=\boxed{\text{ソ}}\space t^2-\boxed{\text{タ}}\space t+\cfrac{\boxed{\text{チ}}}{\boxed{\text{ツ}}}$
であり, $\overrightarrow{\text{PQ}}$ と $\overrightarrow{\text{PR}}$ のなす角を $\theta$ とすると, $S=\cfrac{1}{2}|\overrightarrow{\text{PQ}}||\overrightarrow{\text{PR}}|\sin\theta$ なので
$4S^2=|\overrightarrow{\text{PQ}}|^2|\overrightarrow{\text{PR}}|^2\sin^2\theta$
$=|\overrightarrow{\text{PQ}}|^2|\overrightarrow{\text{PR}}|^2-|\overrightarrow{\text{PQ}}|^2|\overrightarrow{\text{PR}}|^2\cos^2\theta$
$=t^2-\cfrac{\boxed{\text{テ}}}{\boxed{\text{ト}}}\space t+\cfrac{\boxed{\text{ナ}}}{\boxed{\text{ニヌ}}}$
である。よって, $S$ は $t=\cfrac{\boxed{\text{ネ}}}{\boxed{\text{ノハ}}}$ のとき最小になる。
SNSでシェア