【スマホで読む・わかりやすい】センター数学IIB2017追試【解説・正解・問題】

第2問　解答・解説

ア イウ エ 3 10 3　オ カ 1 3　キ 3

クケコ －13　サ 1　シ ス 3 4

セソ タ －2 3　チ ツ 2 4　テ ト 2 2

ナニ ヌ －2 0　ネ,ノ 0,2　ハ 5

ヒ フヘ ホ 3 87 6

(1)

$f'(x)=3x^2-10x+3$

・・・アイウエ

$3x^2-10x+3=0$ とおくと

$(x-3)(3x-1)=0$

$x=3,\cfrac{1}{3}$

$\def\arraystretch{1.25}\begin{array}{c:c:c:c:c:c:c} x &0& \cdots & \frac{1}{3}&\cdots&3&\cdots \\ \hline f'(x) &+ &+ & 0&-&0&+ \\ \hline f(x) &-4 &\nearrow & -\frac{95}{27} &\searrow&-13&\nearrow \end{array}$

$f(0)=-4$

$f\Big(\cfrac{1}{3}\Big)=\cfrac{1}{27}-\cfrac{5}{9}+1-4=-\cfrac{95}{27}$

$f(3)=27-45+9-4=-13$

したがって，$f(x)$ は $x=\cfrac{1}{3}$ で極大値，$x=3$ で極小値をとる。また，$x$ ≧ 0 の範囲における $f(x)$ の最小値は $-13$

・・・オカキクケコ

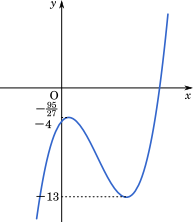
さらに，上の図より，実数解の個数は 1 個。

・・・サ

(2)

$f'(0)=3$ より，$x=0$ における接線の傾きは 3

これが (0，―4) を通るので

$\ell$：$y=3x-4$

・・・シス

また，$C$ を $x$ で微分すると

$y’=2x+p$

$C$ は点 ($a$，$3a-4$) で $\ell$ と接するので

$x=a$ のとき，接線の傾きは $2a+p$ だから

$2a+p=3$

が成り立つ。式を変形して

$p=-2a+3$

・・・セソタ

これと ($a$，$3a-4$) を $C$ に代入して

$3a-4=a^2+(-2a+3)a+q$

$q=3a-4-a^2-(-2a+3)a$

$=a^2-4$

・・・チツ

(3)

$g(x)=x^2+px+q$ とおくと

$g(0)g(1)=q(1+p+q)$

$=(a^2-4)(1-2a+3+a^2-4)$

$=(a^2-4)(a^2-2a)$

$=a(a+2)(a-2)^2$ ＜ 0

・・・テト

$(a-2)^2$ は常に正の値をとるので，不等式を $(a-2)^2$ で割ると

$a(a+2)$ ＜ 0

―2 ＜ $a$ ＜ 0

・・・ナニヌ

また，$g(0)=q=a^2-4=(a+2)(a-2)$

0 ＜ $a+2$ ＜ 2，－4 ＜ $a-2$ ＜ －2

正の数×負の数＝負の数だから，$g(0)$ ＜ 0

・・・ネ

さらに，$g(1)=1+p+q=a^2-2a=a(a-2)$

－2 ＜ $a$ ＜ 0，－4 ＜ $a-2$ ＜ －2

負の数×負の数＝正の数だから，$g(1)$ ＞ 0

・・・ノ

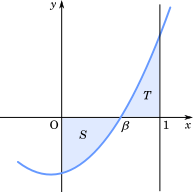
$\displaystyle\int_0^1 g(x)=-S+T=T-S$

また，$S=T$ のとき $T-S=0$ となるので

$\displaystyle\int_0^1 g(x)=0$

が成り立つ。

・・・ハ

$\displaystyle\int_0^1 x^2+(-2a+3)x+a^2-4\space dx$

$=\Big[\cfrac{x^3}{3}+\cfrac{-2a+3}{2}x^2+(a^2-4)x\Big]_0^1$

$=\cfrac{1}{3}+\cfrac{-2a+1}{2}+a^2-4=0$

両辺を 6 倍して

$2-6a+9+6a^2-24=0$

$6a^2-6a-13=0$

$a=\cfrac{3\pm\sqrt{9+78}}{6}$

－2 ＜ $a$ ＜ 0 と，$\sqrt{9}$ ＜ $\sqrt{87}$ $\iff$ $3$ ＜ $\sqrt{87}$ より

$a=\cfrac{3-\sqrt{87}}{6}$

・・・ヒフヘホ

第2問　問題文

関数 $f(x)=x^3-5x^2+3x-4$ について考える。

(1) 関数 $f(x)$ の増減を調べよう。$f(x)$ の導関数は

$f(x)=\boxed{\text{ア}}x^2-\boxed{\text{イウ}}x+\boxed{\text{エ}}$

であり, $f(x)$ は $x=\cfrac{\boxed{\text{オ}}}{\boxed{\text{カ}}}$ で極大値, $x=\boxed{\text{キ}}$ で極小値をとる。よって, $x\geqq0$ の範囲における $f(x)$ の最小値は $\boxed{\text{クケコ}}$ である。

また, 方程式 $f(x)=0$ の異なる実数解の個数は, $\boxed{\text{サ}}$ 個である。

(2) 曲線 $y=f(x)$ 上 の 点 $(0,f(0))$ における接線を $\ell$ とすると, $\ell$ の方程式は $y=\boxed{\text{シ}}x-\boxed{\text{ス}}$ である。また, 放物線 $y=x^2+px+q$ を $C$ とし, $C$ は点$(a, \boxed{\text{シ}}a-\boxed{\text{ス}})$ で $\ell$ と接しているとする。このとき, $p,q$ は $a$ を用いて,

$p=\boxed{\text{セソ}}a+\boxed{\text{タ}},q=a^{\boxed{\text{チ}}}-\boxed{\text{ツ}}$

と表される。

(3) (2)の放物線 $C$ は, $0\leqq x\leqq1$ の範囲では, $x$ 軸とただ1点$(\beta, 0)$で交わり, $0\lt\beta\lt1$ であるとする。このとき, $g(x)=x^2+px+q$ とおけば

$g(0)g(1)=a(a+\boxed{\text{テ}})(a-\boxed{\text{ト}})^2\lt0$

である。$(a-\boxed{\text{ト}})^2$ は負にならないので, $a$ の値の範囲は $\boxed{\text{ナニ}}\lt a\lt \boxed{\text{ヌ}}$ であり, $g(0)\boxed{\text{ネ}}0$, $g(1)\boxed{\text{ノ}}0$ である。ただし, $\boxed{\text{ネ}}$ と $\boxed{\text{ノ}}$ については, 当てはまるものを, 次の⓪~②のうちから一つずつ選べ。同じものを選んでもよい。

⓪ $\lt$　① $=$　② $\gt$

放物線 $C$の $0\leqq x\leqq\beta$ の部分と, $x$ 軸および $y$ 軸で囲まれた図形の面積を $S$ とする。また, $C$ の $\beta\leqq x\leqq1$ の部分と, $x$ 軸および直線 $x=1$ で囲まれた図形の面積を $T$ とする。このとき, $a$ の値によらず, $\displaystyle\int_0^1 g(x)dx=\boxed{\text{ハ}}$ が成り立つ。$\boxed{\text{ハ}}$ に当てはまるものを, 次の⓪~⑦のうちから一つ選べ。

⓪ $S+T$　① $\cfrac{S+T}{2}$

② $2S+T$　③ $2T+S$

④ $S-T$　⑤ $T-S$

⑥ $2S-T$　⑦ $2T-S$

したがって, $S=T$ となる $a$ の値を求めると, $a=\cfrac{\boxed{\text{ヒ}}-\sqrt{\boxed{\text{フヘ}}}}{\boxed{\text{ホ}}}$ ある。