【スマホで読む・わかりやすい】センター数学IIB2017追試【解説・正解・問題】
解答・解説
ア イ 1 2 ウ 6 エ,オ,カ キ 3, 6, 2 3
ク 3 ケ 2 コ,サ 3, 3
シ ス セ 2 3 3 ソタ 12 チ 4 ツ 0
テ,ト 0,2 ナ 0 ニ ヌ ネ 5 2 1
ノ ハ 2 5 ヒ フ 5 2
〔1〕
(1)
公式 $\sin^2x+\cos^2x=1$ より,①は
$2\{1-\sin^2(\beta-\alpha)\}=3\sin(\beta-\alpha)$
$2(1-t^2)=3t$
$2t^2+3t-2=0$
$(t+2)(2t-1)=0$
$t=-2$,$\cfrac{1}{2}$
ここで
-1 ≦ $\sin(\beta-\alpha)$ ≦ 1
-1 ≦ $t$ ≦ 1
だから
$t=\cfrac{1}{2}$
・・・アイ
よって
$\sin(\beta-\alpha)=\cfrac{1}{2}$
$\beta-\alpha=\cfrac{\pi}{6}$
・・・ウ
(2)
$\beta-\alpha=\cfrac{\pi}{6}$ を変形すると $\beta=\alpha+\cfrac{\pi}{6}$ だから
$y=4\sin^2\beta-4\cos^2\alpha$
$=4\sin^2\Big(\alpha+\cfrac{\pi}{6}\Big)-4\cos^2\alpha$
ここで, 加法定理より
$\sin\Big(\alpha+\cfrac{\pi}{6}\Big)=\sin\alpha\cos\cfrac{\pi}{6}+\cos\alpha\sin\cfrac{\pi}{6}$
$=\cfrac{\sqrt{3}}{2}\sin\alpha+\cfrac{1}{2}\cos\alpha$
よって
$\sin^2\Big(\alpha+\cfrac{\pi}{6}\Big)=\Big(\cfrac{\sqrt{3}}{2}\sin\alpha+\cfrac{1}{2}\cos\alpha\Big)^2$
$=\cfrac{3}{4}\sin^2\alpha+\cfrac{\sqrt{3}}{2}\sin\alpha\cos\alpha+\cfrac{1}{4}\cos^2\alpha$
これを $y$ の式に代入すると
$y=4\Big\{\cfrac{3}{4}\sin^2\alpha+\cfrac{\sqrt{3}}{2}\sin\alpha\cos\alpha+\cfrac{1}{4}\cos^2\alpha\Big\}-4\cos^2\alpha$
$=3\sin^2\alpha+2\sqrt{3}\sin\alpha\cos\alpha+\cos^2\alpha-4\cos^2\alpha$
$=3(1-\cos^2\alpha)+2\sqrt{3}\sin\alpha\cos\alpha+\cos^2\alpha-4\cos^2\alpha$
$3-3\cos^2\alpha+2\sqrt{3}\sin\alpha\cos\alpha+\cos^2\alpha-4\cos^2\alpha$
$=3-6\cos^2\alpha+2\sqrt{3}\sin\alpha\cos\alpha\cdots\cdots$②
・・・エオカキ
$y=3$ になるとき
$3-6\cos^2\alpha+2\sqrt{3}\sin\alpha\cos\alpha=3$
$-6\cos^2\alpha+2\sqrt{3}\sin\alpha\cos\alpha=0$
$3\cos^2\alpha-\sqrt{3}\sin\alpha\cos\alpha=0$
$\cos\alpha(3\cos\alpha-\sqrt{3}\sin\alpha)=0$
$\cos\alpha=0$,$3\cos\alpha-\sqrt{3}\sin\alpha=0$
ここで,$\cos\alpha=0$ とすると $\alpha=\cfrac{\pi}{2}$ となる。よって,$\beta=\cfrac{\pi}{2}+\cfrac{\pi}{6}$ ≧ $\cfrac{\pi}{2}$ となるため,不適。
したがって,$3\cos\alpha-\sqrt{3}\sin\alpha=0$
$3\cos\alpha=\sqrt{3}\sin\alpha$
$\cfrac{\sin\alpha}{\cos\alpha}=\cfrac{3}{\sqrt{3}}=\sqrt{3}$
$\tan\alpha=\sqrt{3}$
$\alpha=\cfrac{\pi}{3}$
・・・ク
よって $\beta=\cfrac{\pi}{3}+\cfrac{\pi}{6}=\cfrac{\pi}{2}$
・・・ケ
(3)
半角の公式と2倍角の公式
$\cos^2x=\cfrac{1+\cos2x}{2}$,$\sin2x=2\sin x\cos x$
を用いて②を変形すると
$y=3-6\cos^2\alpha+2\sqrt{3}\sin\alpha\cos\alpha$
$=3-6\Big(\cfrac{1+\cos2\alpha}{2}\Big)+\sqrt{3}\sin2x$
$=3-3-3\cos2\alpha+\sqrt{3}\sin2x$
$=\sqrt{3}\sin2\alpha-3\cos2\alpha$
・・・コサ
さらに,三角関数の合成の公式 $a\sin x+b\cos x=r\sin(x+\alpha)$ を用いて
$\sqrt{3}$:3=3:$3\sqrt{3}$=1:$\sqrt{3}$ だから
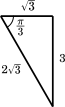
$y=2\sqrt{3}\sin\Big(2\alpha-\cfrac{\pi}{3}\Big)$
・・・シスセ
また,$y=-\sqrt{3}$ のとき
$2\sqrt{3}\sin\Big(2\alpha-\cfrac{\pi}{3}\Big)=-\sqrt{3}$
$\sin\Big(2\alpha-\cfrac{\pi}{3}\Big)=-\cfrac{1}{2}$
ここで
0 ≦ $\alpha$ ≦ $\cfrac{\pi}{2}$
0 ≦ $2\alpha$ ≦ $\pi$
$-\cfrac{\pi}{3}$ ≦ $2\alpha-\cfrac{\pi}{3}$ ≦ $\cfrac{2}{3}\pi$
$\sin$ の値が $-\sqrt{3}$ となるのは第3象限と第4象限だが,これにより第4象限であることが分かる。
$2\alpha-\cfrac{\pi}{3}=-\cfrac{\pi}{6}$
$2\alpha=\cfrac{\pi}{6}$
$\alpha=\cfrac{\pi}{12}$
・・・ソタ
また,$\beta=\alpha+\cfrac{\pi}{6}$ より
$\beta=\cfrac{\pi}{12}+\cfrac{\pi}{6}=\cfrac{\pi}{4}$
・・・チ
〔2〕
(1)
真数条件(真数は正の値)より
$3^x-\Big(\cfrac{1}{3}\Big)^x$ > 0
$3^x$ > $\cfrac{1}{3^x}$
$3^{2x}$ > 1
$9^x$ > 1
$x$ > 0
・・・ツ
同様に,$y$ > 0
次に,$x$ < $y$ のとき
$3^x$ < $3^y$
・・・テ
また,$\Big(\cfrac{1}{3}\Big)^x=\cfrac{1}{3^x}$,$\Big(\cfrac{1}{3}\Big)^y=\cfrac{1}{3^y}$ だから
$\Big(\cfrac{1}{3}\Big)^x$ > $\Big(\cfrac{1}{3}\Big)^y$
・・・ト
上の不等式を足すと
$3^x+\Big(\cfrac{1}{3}\Big)^y$ < $3^y+\Big(\cfrac{1}{3}\Big)^x$
$3^x-\Big(\cfrac{1}{3}\Big)^x$ < $3^y-\Big(\cfrac{1}{3}\Big)^y$
したがって,$p$ < $q$
・・・ナ
(2)
$x=\log_34$ のとき,$3^x=4$ だから
$p=\log_3\Big(4-\cfrac{1}{4}\Big)$
$=\log_3\cfrac{15}{4}$
$=\log_315-\log_34$
$=\log_3(3\cdot5)-\log_32^2$
$=\log_33+\log_35-2\log_32$
$=\log_35-2\log_32+1$
・・・ニヌネ
また,$p=\log_34$ のとき
$3^x-\Big(\cfrac{1}{3}\Big)^x=4$
$\cfrac{3^{2x}-1}{3^x}=4$
$3^{2x}-1=4\cdot3^x$
$3^{2x}-4\cdot3^x-1=0$
$3^x=t$ とおくと
$t^2-4t-1=0$
$t=2\pm\sqrt{4+1}=2\pm\sqrt{5}$
$3^x=2\pm\sqrt{5}$
$x$ > 0 より
$3^x=2+\sqrt{5}$
$x=\log_3(2+\sqrt{5})$
・・・ノハ
(3)
$y=2x-1$,$q=2p-1$ を $q$ の式に代入すると
$2\log_3\Big\{3^x-\Big(\cfrac{1}{3}\Big)^x\Big\}-1=\log_3\Big\{3^{2x-1}-\Big(\cfrac{1}{3}\Big)^{2x-1}\Big\}$
$\log_3\Big\{3^x-\Big(\cfrac{1}{3}\Big)^x\Big\}^2=\log_3\Big\{3^{2x-1}-\Big(\cfrac{1}{3}\Big)^{2x-1}\Big\}+1$
$\log_3\Big\{3^x-\Big(\cfrac{1}{3}\Big)^x\Big\}^2=\log_3\Big\{3^{2x-1}-\Big(\cfrac{1}{3}\Big)^{2x-1}\Big\}+\log_3 3$
$\log_3\Big\{3^x-\Big(\cfrac{1}{3}\Big)^x\Big\}^2=\log_33\Big\{3^{2x-1}-\Big(\cfrac{1}{3}\Big)^{2x-1}\Big\}$
$\log_3\Big\{3^x-\Big(\cfrac{1}{3}\Big)^x\Big\}^2=\log_3\Big\{3^{2x}-3\Big(\cfrac{1}{3}\Big)^{2x-1}\Big\}$
$\Big\{3^x-\Big(\cfrac{1}{3}\Big)^x\Big\}^2=3^{2x}-3\Big(\cfrac{1}{3}\Big)^{2x-1}$
$3^{2x}-2\cdot3^x\Big(\cfrac{1}{3}\Big)^{x}+\Big(\cfrac{1}{3}\Big)^{2x}=3^{2x}-3\Big(\cfrac{1}{3}\Big)^{2x-1}$
$-2\cdot3^x\Big(\cfrac{1}{3}\Big)^{x}+\Big(\cfrac{1}{3}\Big)^{2x}=-3\Big(\cfrac{1}{3}\Big)^{2x-1}$
$3\Big(\cfrac{1}{3}\Big)^{2x-1}+\Big(\cfrac{1}{3}\Big)^{2x}=2$
$\Big(\cfrac{1}{3}\Big)^{2x}\Big\{3\Big(\cfrac{1}{3}\Big)^{-1}+1\Big\}=2$
$\Big(\cfrac{1}{3}\Big)^{2x}(3\cdot3+1)=2$
$\Big(\cfrac{1}{3}\Big)^{2x}\cdot10=2$
$\Big(\cfrac{1}{3}\Big)^{2x}=\cfrac{1}{5}$
$\cfrac{1}{3^{2x}}=\cfrac{1}{5}$
$3^{2x}=5$
$2x=\log_3 5$
$x=\cfrac{\log_35}{2}$
・・・ヒフ
第1問 問題文
〔1〕$0\leqq a\leqq \cfrac{\pi}{2}$, $0\leqq\beta\leqq\cfrac{\pi}{2}$ および関係式
$2\cos^2(\beta-\alpha)=3\sin(\beta-\alpha)\cdots\cdots$①
を満たす $\alpha,\beta$ に対して, $y=4\sin^2\beta-4\cos^2 \alpha$ とおく。
(1) $t=\sin(\beta-\alpha)$ とおくと, ①から $t=\cfrac{\boxed{\text{ア}}}{\boxed{\text{イ}}}$ であることがわかる。
$0\leqq\alpha\leqq\cfrac{\pi}{2}$, $0\leqq\beta\leqq\cfrac{\pi}{2}$ であるから, $\beta-\alpha=\cfrac{\pi}{\boxed{\text{ウ}}}$ である。
(2) (1)により $\beta=\alpha+\cfrac{\pi}{\boxed{\text{ウ}}}$ であるから, 加法定理を用いて, $y$ を $\alpha$ で表すと
$y=\boxed{\text{エ}}-\boxed{\text{オ}}\space\cos^2\alpha+\boxed{\text{カ}}\sqrt{\boxed{\text{キ}}}\space\sin\alpha\cos\alpha\cdots$②
となる。このことから, $y=\boxed{\text{エ}}$ となるのは, $a=\cfrac{\pi}{\boxed{\text{ク}}}$, $\beta=\cfrac{\pi}{\boxed{\text{ケ}}}$ のときである。
(3) 2倍角の公式を用いると, ②は
$y=\sqrt{\boxed{\text{コ}}}\space\sin2\alpha-\boxed{\text{サ}}\cos2\alpha$
となる。さらに, 三角関数の合成を用いると
$y=\boxed{\text{シ}}\sqrt{\boxed{\text{ス}}}\sin\Big(2\alpha-\cfrac{\pi}{\boxed{\text{セ}}}\Big)$
と変形できる。このことから, $y=-\sqrt{3}$ となるのは, $\alpha=\cfrac{\pi}{\boxed{\text{ソタ}}}$, $\beta=\cfrac{\pi}{\boxed{\text{チ}}}$ のときである。
〔2〕$p,q,x,y$ は実数とし, 関係式
$p=\log_3\Big\{3^x-\Big(\cfrac{1}{3}\Big)^x\Big\}$, $q=\log_3\Big\{3^y-\Big(\cfrac{1}{3}\Big)^y\Big\}$
を満たすとする。
(1) 真数の条件により, $x\gt\boxed{\text{ツ}}$, $y\gt\boxed{\text{ツ}}$ である。ただし, 対数 $log_a b$ に対し, $a$ を底といい, $b$ を真数という。
また, $x\lt y$ であるとき
$3^x\boxed{\text{テ}}3^y$, $\Big(\cfrac{1}{3}\Big)^x\boxed{\text{ト}}\Big(\cfrac{1}{3}\Big)^y$, $p\boxed{\text{ナ}}q$
が成り立つ。$\boxed{\text{テ}},\boxed{\text{ト}},\boxed{\text{ナ}}$ に当てはまるものを, 次の⓪~②のうちから一つずつ選べ。ただし, 同じものを繰り返し選んでもよい。
⓪ $\lt$ ① $=$ ② $\gt$
(2) $x=\log_3 4$ のとき, $p=\log_3\boxed{\text{ニ}}-\boxed{\text{ヌ}}\log_3 2+\boxed{\text{ネ}}$ であ る。また, $p=\log_3 4$のとき, $x=\log_3\Big(\boxed{\text{ノ}}+\sqrt{\boxed{\text{ハ}}}\Big)$ である。
(3) 関係式 $y=2x-1$, $q=2p-1$ が成り立つとき, $x=\cfrac{\log_3\boxed{\text{ヒ}}}{\boxed{\text{フ}}}$ である。
SNSでシェア