【スマホで読む・わかりやすい】センター数学IIB2017本試【解説・正解・問題】

第4問　解答・解説

ア,イ 1, 3　ウ 2　エ オ, カ キ 5 2, 3 2

ク,ケ 1, 3　コ サ 4 3　シ ス 2 3

セ ソ,タ チ ツ 4 3, 2 3 3　テ,ト ナ 2, a 3

ニ ヌ ネ ノ, ハ － 2 1 2, a

ヒ フヘ 5 12

(1)

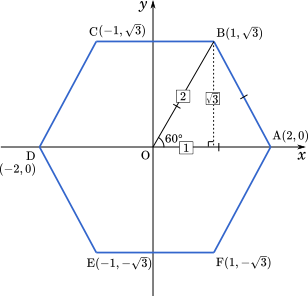
∠AOB＝60° だから，上の図より

B(1, $\sqrt{3}$)，D(－2, 0)

・・・アイウ

(2)

M は BD の中点だから

$\overrightarrow{\text{OM}}=\Big(\cfrac{1-2}{2},\cfrac{\sqrt{3}+0}{2}\Big)$

$=\Big(-\cfrac{1}{2},\cfrac{\sqrt{3}}{2}\Big)$

$\overrightarrow{\text{AM}}=\overrightarrow{\text{OM}}-\overrightarrow{\text{OA}}$ より

$\overrightarrow{\text{AM}}=\Big(-\cfrac{1}{2}-2,\cfrac{\sqrt{3}}{2}-0\Big)$

$=\Big(-\cfrac{5}{2},\cfrac{\sqrt{3}}{2}\Big)$

・・・エオカキ

また

$\overrightarrow{\text{DC}}=\overrightarrow{\text{OC}}-\overrightarrow{\text{OD}}$ より

$\overrightarrow{\text{DC}}=(-1,\sqrt{3})-(-2,0)$

$=(1,\sqrt{3})$

・・・クケ

よって $\overrightarrow{\text{ON}}$ は

$\overrightarrow{\text{ON}}=\overrightarrow{\text{OA}}+r\overrightarrow{\text{AM}}$

$=(2,0)+r\Big(-\cfrac{5}{2},\cfrac{\sqrt{3}}{2}\Big)$

$=\Big(2-\cfrac{5}{2}r,\cfrac{\sqrt{3}}{2}r\Big)$

$\overrightarrow{\text{ON}}=\overrightarrow{\text{OD}}+s\overrightarrow{\text{DC}}$

$=(-2,0)+s(1,\sqrt{3})$

$=(-2+s,\sqrt{3}s)$

座標を比べると

$2-\cfrac{5}{2}r=-2+s$

$4-5r=-4+2s$

$5r=8-2s$

また

$\cfrac{\sqrt{3}}{2}r=\sqrt{3}s$

$r=2s$

式を連立して

$5\cdot2s=8-2s$

$12s=8$

$s=\cfrac{2}{3}$

・・・シス

$r=2s$ に代入して

$r=2\cdot\cfrac{2}{3}=\cfrac{4}{3}$

・・・コサ

したがって，$\overrightarrow{\text{ON}}$ は

$\overrightarrow{\text{ON}}=\Big(-2+\cfrac{2}{3},\sqrt{3}\cdot\cfrac{2}{3}\Big)$

$=\Big(-\cfrac{4}{3},\cfrac{2\sqrt{3}}{3}\Big)$

・・・セソタチツ

(3)

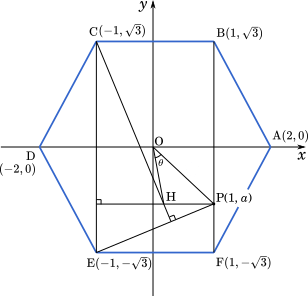
$\overrightarrow{\text{EP}}=\overrightarrow{\text{OP}}-\overrightarrow{\text{OE}}$

$=(1,a)-(-1,-\sqrt{3})$

$=(2,a+\sqrt{3})$

・・・テトナ

次に H の座標を求める。CH と EP は垂直だから

$\overrightarrow{\text{CH}}$・$\overrightarrow{\text{EP}}=0$

H の座標を $(x,a)$ とおくと，

$\overrightarrow{\text{CH}}=\overrightarrow{\text{OH}}-\overrightarrow{\text{OC}}$

$=(x,a)-(-1,\sqrt{3})$

$=(x+1,a-\sqrt{3})$

よって

$\overrightarrow{\text{CH}}$・$\overrightarrow{\text{EP}}$

＝$(x+1)\cdot2+(a-\sqrt{3})(a+\sqrt{3})=0$

$2x+2+a^2-3=0$

$2x=-a^2+1$

$x=\cfrac{-a^2+1}{2}$

したがって，H の座標は

$\Big(\cfrac{-a^2+1}{2},a\Big)$

・・・ニヌネノハ

さらに，$a$ の値を求めると，内積を用いて

$\overrightarrow{\text{OP}}$・$\overrightarrow{\text{OH}}$＝$|\overrightarrow{\text{OP}}||\overrightarrow{\text{OH}}|\cos\theta$

三平方の定理を用いて $|\overrightarrow{\text{OP}}|$ を求めると

$|\overrightarrow{\text{OP}}|=\sqrt{a^2+1}$

また，$|\overrightarrow{\text{OH}}|$ は

$|\overrightarrow{\text{OH}}|=\sqrt{\Big(\cfrac{-a^2+1}{2}\Big)^2+a^2}$

$=\sqrt{\cfrac{a^4-2a^2+1}{4}+a^2}$

$=\sqrt{\cfrac{a^4+2a^2+1}{4}}$

$=\cfrac{\sqrt{(a^2+1)^2}}{2}$

$=\cfrac{a^2+1}{2}$

よって

$\overrightarrow{\text{OP}}$・$\overrightarrow{\text{OH}}$＝$\sqrt{a^2+1}\cdot\cfrac{a^2+1}{2}\cdot\cfrac{12}{13}$

また，成分表示を用いて内積を表すと

$\overrightarrow{\text{OP}}$・$\overrightarrow{\text{OH}}$＝$1\cdot\cfrac{-a^2+1}{2}+a^2$

$=\cfrac{a^2+1}{2}$

よって

$\sqrt{a^2+1}\cdot\cfrac{a^2+1}{2}\cdot\cfrac{12}{13}$＝$\cfrac{a^2+1}{2}$

$\sqrt{a^2+1}\cdot\cfrac{12}{13}=1$

$\sqrt{a^2+1}=\cfrac{13}{12}$

$a^2+1=\cfrac{169}{144}$

$a^2=\cfrac{25}{144}$

$a=\pm\cfrac{5}{12}$

・・・ヒフヘ

第4問　問題文

座標平面上に点A$(2,0)$ をとり,原点 O を中心とする半径が 2 の円周上に 点 B, C, D, E, F を, 点 A, B, C, D, E, F が順に正六角形の頂点となるようにとる。ただし, Bは第 1 象限にあるとする。

(1) 点 B の座標は $(\boxed{\text{コ}},\sqrt{\boxed{\text{イ}}})$, 点 D の座標は $(-\boxed{\text{ウ}},0)$ である。

(2) 線分 BD の中点を M とし,　直線 AM と直線 CD の交点を N とする。$\overrightarrow{\text{ON}}$ を求めよう。

$\overrightarrow{\text{ON}}$ は実数 $r, s$ を用いて, $\overrightarrow{\text{ON}} = \overrightarrow{\text{OA}} + r \overrightarrow{\text{AM}}$, $\overrightarrow{\text{ON}} = \overrightarrow{\text{OD}} + s \overrightarrow{\text{DC}}$ と 2 通りに表すことができる。ここで

$\overrightarrow{\text{AM}}=\bigg(-\cfrac{\boxed{\text{エ}}}{\boxed{\text{オ}}},\cfrac{\sqrt{\boxed{\text{カ}}}}{\boxed{\text{キ}}}\bigg)$

$\overrightarrow{\text{DC}}=(\boxed{\text{ク}},\sqrt{\boxed{\text{ケ}}})$

であるから

$r=\cfrac{\boxed{\text{コ}}}{\boxed{\text{サ}}},\enspace s=\cfrac{\boxed{\text{シ}}}{\boxed{\text{ス}}}$

である。よって

$\overrightarrow{\text{ON}}=\bigg(-\cfrac{\boxed{\text{セ}}}{\boxed{\text{ソ}}},\cfrac{\boxed{\text{タ}}\sqrt{\boxed{\text{チ}}}}{\boxed{\text{ツ}}}\bigg)$

である。

(3) 線分 BF 上に点Pをとり, その $y$ 座標を $a$ とする。点 P から直線 CE に引いた垂線と点 C から直線 EP に引いた垂線との交点を H とする。

$\overrightarrow{\text{EP}}=(\boxed{\text{テ}},\enspace\boxed{\text{ト}}+\sqrt{\boxed{\text{ナ}}})$

と表せることにより, H の座標を $a$ を用いて表すと

$\bigg(\cfrac{\boxed{\text{ニ}}a^{\boxed{\text{ヌ}}}+\boxed{\text{ネ}}}{\boxed{\text{ノ}}},\enspace\boxed{\text{ハ}}\bigg)$

である。

さらに, $\overrightarrow{\text{OP}}$ と $\overrightarrow{\text{OH}}$ のなす角を $\theta$ とする。$\cos \theta = \cfrac{12}{13}$ のとき, $a$ の値は

$a=\pm\cfrac{\boxed{\text{ヒ}}}{\boxed{\text{フヘ}}}$

である。