【スマホで読む・わかりやすい】センター数学IIB2017本試【解説・正解・問題】

第2問　解答・解説

ア 2　イ 1　ウ エ オ 2 2 1　カ キ 2 1

ク 1　ケ 1　コ サ シ ス 4 2 4 4

セ 2　ソ タ 0 1　チ ツ テ 2 2 3　ト ナ 2 3

ニ ヌネ 8 27　ノ ハ ヒ 7 3 3

フ a　ヘ 2

(1)

$y=x^2+1$ を $x$ で微分すると

$y’=2x$

よって，$x=t$ のときの接線の傾きは $2t$

接線は$(t,t^2+1)$を通るので，方程式は

$y-(t^2-1)=2t(x-t)$

$y=2tx-2t^2+t^2+1$

$=2tx-t^2+1$

・・・アイ

これが P$(a,2a)$ を通過するので，それぞれ $x,y$ に代入すると

$2a=2ta-t^2+1$

$t^2-2at+2a-1=0$

・・・ウエオ

$(t-2a+1)(t-1)=0$

$t=2a-1,1$

・・・カキク

ここで $a=1$ とすると，$2a-1=1$ となり，$t$ は重解となる。接線が 2 本あるとき，$t$ は異なる 2 つの実数解を持つので，$a$ ≠ 1

・・・ケ

2 本の接線を求めると

(i) $t=2a-1$ のとき

$y=2tx-t^2+1$ に代入して

$y=2(2a-1)x-(2a-1)^2+1$

$=(4a-2)x-4a^2+4a-1+1$

$=(4a-2)x-4a^2+4a\cdots\cdots$①

・・・コサシス

(ii) $t=1$ のとき

$y=2x-1+1=2x$

・・・セ

(2)

$r$ を $r=-4a^2+4a$ とすると

$r$ ＞ 0 のとき

$-4a^2+4a$ ＞ 0

$a^2-a$ ＜ 0

$a(a-1)$ ＜ 0

0 ＜ $a$ ＜ 1

・・・ソタ

△OPR の面積 $S$ を求めると

$S=\cfrac{1}{2}ra$

$=\cfrac{1}{2}(-4a^2+4a)a$

$=-2a^3+2a^2$

$=2(a^2-a^3)$

・・・チツテ

また，0 ＜ $a$ ＜ 1 のとき，$S$ の増減を調べると

$S’=2(2a-3a^2)$

$2a(2a-3a^2)=0$ とおくと

$2a-3a^2=0$

$a$ ＞ 0 より

$2-3a=0$

$a=\cfrac{2}{3}$

$\def\arraystretch{1.25}\begin{array}{|c|c|c|c|}a & \cdots&\frac{2}{3}&\cdots\\\hline S’ &+&0&-\\\hline S&\nearrow&\text{最大}&\searrow\end{array}$

$a=\cfrac{2}{3}$ のとき

$S=2\Big\{\Big(\cfrac{2}{3}\Big)^2-\Big(\cfrac{2}{3}\Big)^3\Big\}$

$=2\Big(\cfrac{4}{9}-\cfrac{8}{27}\Big)^2$

$=2\cdot\cfrac{4}{27}=\cfrac{8}{27}$

・・・トナニヌネ

(3)

0 ＜ $a$ ＜ 1 のとき

$\displaystyle T=\int_0^\alpha x^2+1-(4a-2)x+4a^2-4a+1\enspace dx$

$=\Big[\cfrac{x^3}{3}-\cfrac{1}{2}(4a-2)x^2+(4a^2-4a+1)x\Big]_0^\alpha$

$=\cfrac{1}{3}a^3-(2a-1)a^2+(4a^2-4a+1)a$

$=\cfrac{1}{3}a^3-3a^2+a$

・・・ノハヒフ

$T$ の増減を調べると

$T’=7a^2-6a+1$

$7a^2-6a+1=0$ とおくと

$(7a+1)(a-1)=0$

$a=1,-\cfrac{1}{7}$

よって，$T$ は 0 ＜ $a$ ＜ 1 の範囲で極値をとらない。，また，0 ＜ $a$ ＜ 1 の範囲で $T’$ は正の値をとるので，$T$ は増加する。

・・・ヘ

第2問　問題文

O を原点とする座標平面上の放物線 $y=x^2 + 1$ を $C$ とし, 点$(a, 2a)$ を P とする。

(1) 点 P を通り, 放物線 $C$ に接する直線の方程式を求めよう。

$C$ 上の点$(t, t^2 + 1)$における接線の方程式は

$y=\boxed{\text{ア}}tx-t^2 +\boxed{\text{イ}}$

である。この直線が P を通るとすると, $t$ は方程式

$t^2-\boxed{\text{ウ}}at+\boxed{\text{エ}}a-\boxed{\text{オ}}=0$

を満たすから, $t=\boxed{\text{カ}}a-\boxed{\text{キ}}$, $\boxed{\text{ク}}$ である。よって, $a\not=\boxed{\text{ケ}}$ のとき, P を通る $C$ の接線は 2 本あり,それらの方程式は

$y=(\boxed{\text{コ}}a-\boxed{\text{サ}})x-\boxed{\text{シ}}a^2+\boxed{\text{ス}}a\cdots\cdots$①

と

$y=\boxed{\text{セ}}x$

である。

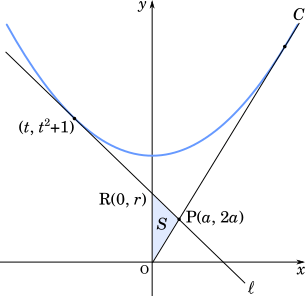
(2) (1)の方程式①で表される直線を $\ell$ とする。$\ell$ と $y$ 軸との交点を R$(0, r)$ とすると, $r=-\boxed{\text{シ}}a^2+\boxed{\text{ス}}a$ である。$r\gt0$ となるのは, $\boxed{\text{ソ}}\lt a\lt\boxed{\text{タ}}$ のときであり, このとき, 三角形 OPR の面積 $S$ は

$S=\boxed{\text{チ}}(a^{\boxed{\text{ツ}}}-a^{\boxed{\text{テ}}})$

となる。

$\boxed{\text{ソ}}\lt a \lt \boxed{\text{タ}}$ のとき, $S$ の増減を調べると, $S$ は $a=\cfrac{\boxed{\text{ト}}}{\boxed{\text{ナ}}}$ で最大値 $\cfrac{\boxed{\text{ニ}}}{\boxed{\text{ヌネ}}}$ をとることがわかる。

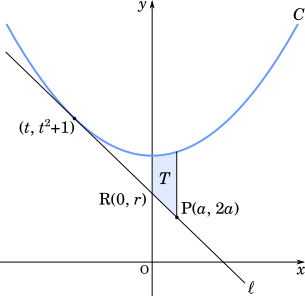
(3) $\boxed{\text{ソ}}\lt a\lt\boxed{\text{タ}}$ のとき, 放物線 $C$ と(2)の 直線 $\ell$ および2直線 $x=0$, $x=a$ で囲まれた図形の面積を $T$ とすると

$T=\cfrac{\boxed{\text{ノ}}}{\boxed{\text{ハ}}}a^3-\boxed{\text{ヒ}}a^2+\boxed{\text{フ}}$

である。$\cfrac{\boxed{\text{ト}}}{\boxed{\text{ナ}}}\leqq a\lt \boxed{\text{タ}}$ の範囲において, $T$ は $\boxed{\text{ヘ}}$。$\boxed{\text{ヘ}}$ に当てはまるものを, 次の⓪~⑤のうちから一つ選べ。

⓪ 減少する　① 極小値をとるが,極大値はとらない

② 増加する　③ 極大値をとるが,極小値はとらない

④ 一定である　⑤ 極小値と極大値の両方をとる