【スマホで読む・わかりやすい】センター数学IIB2017本試【解説・正解・問題】

第1問　解答・解説

アイ　ウエ　17 15　オ 4 　カ キ 4 5

ク ケ 1 3　コ サ シ 2 5 5　ス セ ソ － 3 3

タ 0　チ ツ 1 3　テ ト ナ 1 3 1

ニ ヌ ネ 1 8 3　ノ ハ 6 6　ヒ フ 2 6

ヘ 6

〔1〕

2 倍角の公式より

$\cos2x=\cos^2x-\sin^2x$

$=\cos^2x-(1-\cos^2x)$

$=2\cos^2-1$

よって，①は

$2\cos^2\alpha-1+2\cos^2\beta-1=\cfrac{4}{15}$

$2\cos^2\alpha+2\cos^2\beta=\cfrac{34}{15}$

$\cos^2\alpha+\cos^2\beta=\cfrac{17}{15}$

・・・アイウエ

また，②の両辺を 2 乗すると

$\cos^2\alpha+\cos^2\beta=\Big(-\cfrac{2\sqrt{15}}{15}\Big)^2$

$=\cfrac{4\cdot15}{15^2}=\cfrac{4}{15}$

・・・オ

ここで，$(x-\cos^2\alpha)(x-\cos^2\beta)=0$ とおくと，方程式の解は $x=\cos^2\alpha$，$\cos^2\beta$ となる。式を展開すると

$x^2-(\cos^2\alpha+\cos^2\beta)x+\cos^2\alpha\cos^2\beta=0$

$x^2-\cfrac{17}{15}x+\cfrac{4}{15}=0$

$15x^2-17x+4=0$

$(3x-1)(5x-4)=0$

$x=\cfrac{1}{3}$，$\cfrac{4}{5}$

③ より

$\cos^2\alpha=\cfrac{4}{5}$，$\cos^2\beta=\cfrac{1}{3}$

・・・カキクケ

また，②を見ると，右辺が負の値だから，左辺の $\cos\alpha$ か $\cos\beta$ のどちらかが負の値である。$\alpha$＜$\beta$ より，$\alpha$ を第1象限(正の値)，$\beta$ を第2象限(負の値)とするとよい。したがって

$\cos\alpha=\sqrt{\cfrac{4}{5}}=\cfrac{2}{\sqrt{5}}=\cfrac{2\sqrt{5}}{5}$

・・・コサシ

$\cos\beta=-\sqrt{\cfrac{1}{3}}=-\cfrac{\sqrt{3}}{3}$

・・・スセソ

〔2〕

真数条件より，$p$ ＞ 0，$q$ ＞ 0

・・・タ

AB を 1：2 に内分する点は

$\bigg(\cfrac{2\cdot0+p}{1+2},\cfrac{2\cdot\small{\dfrac{3}{2}}+\log_2p}{1+2}\bigg)$

$=\Big(\cfrac{1}{3}p,\cfrac{1}{3}\log_2p+1\Big)$

・・・チツテトナ

これが C の座標と一致するので

$\begin{cases}\cfrac{1}{3}p=q\cdots\cdots\text{④}\\\cfrac{1}{3}\log_2p+1=\log_2 q\cdots\cdots\text{⑤}\end{cases}$

⑤を変形すると

$\log_2p+3=3\log_2q$

$\log_2p=3\log_2q-3$

$\log_2p=\log_2q^3-\log_28$

$\log_2p=\log_2\cfrac{q^3}{8}$

$p=\cfrac{1}{8}q^3\cdots\cdots$⑥

・・・ニヌネ

④と⑥を連立して

$p=\cfrac{1}{8}\Big(\cfrac{1}{3}p\Big)^3$

$p=\cfrac{p^3}{2^3\cdot3^3}$

$2^3\cdot3^3p=p^3$

$p$ ＞ 0 より

$p^2=2^3\cdot3^3$

$p=\sqrt{2^3\cdot3^3}=6\sqrt{6}$

・・・ノハ

④に代入して

$\cfrac{1}{3}\cdot6\sqrt{6}=q$

$q=2\sqrt{6}$

・・・ヒフ

次に，$\log_22\sqrt{6}$ の値を求めると

$\log_22\sqrt{6}=\log_2(2\cdot\sqrt{2}\cdot\sqrt{3})$

$=\log_22+\log_2\sqrt{2}+\log_2\sqrt{3}$

$=1+\log_22^{\small{\frac{1}{2}}}+\log_23^{\small{\frac{1}{2}}}$

$=1+\cfrac{1}{2}\log_22+\cfrac{1}{2}\log_23$

$=1+\cfrac{1}{2}+\cfrac{1}{2}\log_23$

$=\cfrac{3}{2}+\cfrac{1}{2}\cdot\cfrac{\log_{10}3}{\log_{10}2}$

$=\cfrac{3}{2}+\cfrac{1}{2}\cdot\cfrac{0.4771}{0.3010}$

$=\cfrac{3}{2}+\cfrac{1}{2}\cdot1.58$

＝ 2.29 ≒ 2.3

・・・ヘ

第1問　問題文

〔1〕連立方程式

$\begin{cases}\cos 2\alpha+\cos 2\beta=\cfrac{4}{15}\cdots\cdots\text{①}\\\cos\alpha\cos\beta=-\cfrac{2\sqrt{15}}{15}\cdots\cdots{\text{②}}\end{cases}$

を考える。ただし, $0\leqq \alpha \leqq x$, $0\leqq\beta\leqq\pi$ であり, $\alpha\lt\beta$ かつ

$|\cos\alpha|\geqq|\cos\beta|\cdots\cdots$③

とする。このとき, $\cos\alpha$ と $\cos\beta$ の値を求めよう。

2 倍角の公式を用いると, ①から

$\cos^2\alpha+\cos^2\beta=\cfrac{\boxed{\text{アイ}}}{\boxed{\text{ウエ}}}$

が得られる。また, ②から, $\cos^2\alpha\cos^2\beta=\cfrac{\boxed{\text{オ}}}{15}$ である。

したがって, 条件③を用いると

$\cos^2\alpha=\cfrac{\boxed{\text{カ}}}{\boxed{\text{キ}}}$, $\cos^2\beta=\cfrac{\boxed{\text{ク}}}{\boxed{\text{ケ}}}$

である。よって, ②と条件 $0\leqq\alpha\leqq\pi$, $0\leqq\beta\leqq\pi$, $\alpha\lt\beta$ から

$\cos\alpha=\cfrac{\boxed{\text{コ}}\sqrt{\boxed{\text{サ}}}}{\boxed{\text{シ}}}$, $\cos\beta=\cfrac{\boxed{\text{ス}}\sqrt{\boxed{\text{セ}}}}{\boxed{\text{ソ}}}$

である。

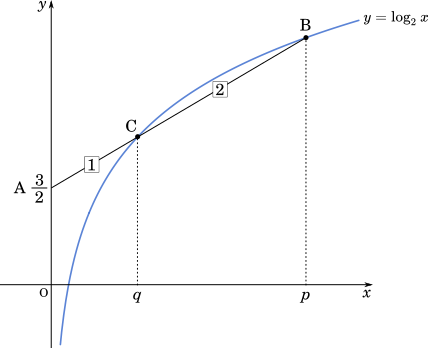
〔2〕座標平面上に点 A$\bigg(0,\cfrac{3}{2}\bigg)$ をとり, 関数 $y=\log_2 x$のグラフ上に 2 点 B$(p,\log_2p)$, C$(q,\log_2q)$をとる。線分 AB を 1 : 2 に内分する点が C であるとき, $p,q$ の値を求めよう。

真数の条件により, $p\gt\boxed{\text{タ}}$, $q\gt\boxed{\text{タ}}$ である。ただし, 対数 $\log_a b$ に対し, $a$ を底といい, $b$ を真数という。

線分 AB を 1 : 2 に内分する点の座標は, $p$ を用いて

$\bigg(\cfrac{\boxed{\text{チ}}}{\boxed{\text{ツ}}}p,\enspace\cfrac{\boxed{\text{テ}}}{\boxed{\text{ト}}}\log_2 p+\boxed{\text{ナ}}\bigg)$

と表される。これが C の座標と一致するので

$\begin{cases}\cfrac{\enspace\boxed{\text{チ}}\enspace}{\boxed{\text{ツ}}}p=q\cdots\cdots\text{④}\\\cfrac{\enspace\boxed{\text{テ}}\enspace}{\boxed{\text{ト}}}\log_2 p+\boxed{\text{ナ}}=\log_2 q\cdots\cdots\text{⑤}\end{cases}$

が成り立つ。

⑤は

$p=\cfrac{\boxed{\text{ニ}}}{\boxed{\text{ヌ}}}q^{\boxed{\text{ネ}}}\cdots\cdots$⑥

と変形できる。④と⑥を連立させた方程式を解いて, $p\gt\boxed{\text{タ}}$ に注意すると

$p=\boxed{\text{ノ}}\sqrt{\boxed{\text{ハ}}}$, $q=\boxed{\text{ヒ}}\sqrt{\boxed{\text{フ}}}$

である。

また, Cの $y$ 座標 $\log_2(\boxed{\text{ヒ}}\sqrt{\boxed{\text{フ}}})$ の値を, 小数第2位を四捨五入して小数第1位まで求めると, $\boxed{\text{ヘ}}$ である。$\boxed{\text{ヘ}}$ に当てはまるものを, 次の⓪~$\text{\textcircled{b}}$のうちから一つ選べ。ただし, $\log_{10}2=0.3010$, $\log_{10}3=0.4771$, $\log_{10}7=0.8451$ とする。

⓪ 0.3　① 0.6　② 0.9　③ 1.3　④ 1.6

⑤ 1.9　⑥ 2.3　⑦ 2.6　⑧ 2.9　⑨ 3.3

$\text{\textcircled{a}}$ 3.6　$\text{\textcircled{b}}$ 3.9