【スマホで読む・わかりやすい】センター数学IIB2016追試【解説・正解・問題】
第2問 解答・解説
ア イ 2 a ウエ オ 2a 1 カ 2
キ ク 2 1 ケコ サ シ -3 2 4
ス セ 2 3 ソタ チ 2a 3 ツ テ a 3
トナ ニ, ヌ -1 9, 1 ネ ノ 2 3
ハ ヒ フヘ 2 3 27
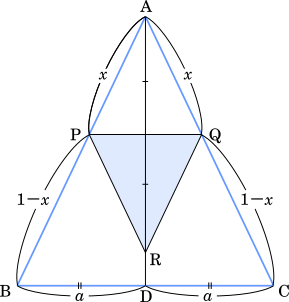
(1)
AB の長さは周の長さから BC の長さを引いたものを 2 で割れば求められる。
AB = $\cfrac{1}{2}(4-2a)=2-a$
・・・アイ
また,BC の中点を D とすると,三平方の定理より
AD = $\sqrt{(2-a)^2-a^2}$
$\sqrt{4-4a+a^2-a^2}=2\sqrt{1-a}$
したがって △ABC の面積は
△ABC=$\cfrac{1}{2}\cdot2a\cdot2\sqrt{1-a}=2a\sqrt{1-a}$
・・・ウエオ
(2)
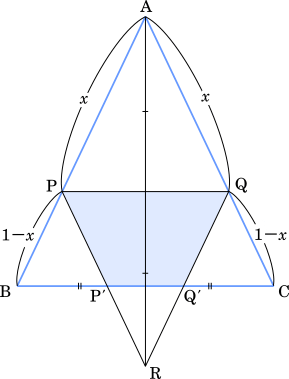
△RPQ の面積を求める。△ABC ∽ △APQ だから,面積の比は $1^2:x^2$ である。また,△APQ=△RPQ だから
△RPQ=$2a\sqrt{1-a}x^2\cdots\cdots$①
・・・カ
さらに,△RPQ と △ABC の共通部分の面積を求める。PQ の中点を E とすると
AD:RE=1:$x$
RE:RD=$x$:$x-(1-x)$=$x$:$(2x-1)$
よって
AD:RD=1:$(2x-1)$
したがって,△RP’Q’ と △ABC の相似比は
$(2x-1)$:1
・・・キク
よって,△RP’Q’ と △ABC の面積比は $(2x-1)^2$:$1^2$ だから,△RP’Q’ の面積は
△RP’Q’=$2a\sqrt{a-1}(2x-1)^2$
共通部分の面積は,△RPQ-△RP’Q’ だから
$f(x)=2a\sqrt{1-a}x^2-2a\sqrt{1-a}(2x-1)^2$
$=2a\sqrt{1-a}\{x^2-(2x-1)^2\}$
$=2a\sqrt{1-a}(x^2-4x^2+4x-1)$
$=2a\sqrt{1-a}(-3x^2+4x-1)$
・・・ケコサシ
最大値を求めるために,式を平方完成すると
$f(x)=2a\sqrt{1-a}\Big\{-3\Big(x^2-\cfrac{4}{3}x\Big)-1\Big\}$
$=2a\sqrt{1-a}\Big\{-3\Big(x-\cfrac{2}{3}\Big)^2+\cfrac{4}{3}-1\Big\}$
$=2a\sqrt{1-a}\Big\{-3\Big(x-\cfrac{2}{3}\Big)^2+\cfrac{1}{3}\Big\}$
$=-6a\sqrt{1-a}\Big(x-\cfrac{2}{3}\Big)^2+\cfrac{2}{3}a\sqrt{1-a}$
したがって,$f(x)$ は $x=\cfrac{2}{3}$ で,最大値 $\cfrac{2a}{3}\sqrt{1-a}$ をとる。
・・・スセソタチ
(3)
$f(x)$ は,0< $x$ ≦ $\cfrac{1}{2}$ のときと $\cfrac{1}{2}$ < $x$ < 1 のときで式が異なることに注意して
$\displaystyle S=\int_{\small{0}}^{\small{\frac{1}{2}}}2a\sqrt{1-a}x^2dx+\displaystyle\int_{\small{\frac{1}{2}}}^1 2a\sqrt{1-a}(-3x^2+4x-1)dx$
$=2a\sqrt{1-a}\Big[\cfrac{x^3}{3}\Big]_{\small{0}}^{\small{\frac{1}{2}}}+2a\sqrt{1-a}\Big[-x^3+2x^2-x\Big]_{\small{\frac{1}{2}}}^1$
$=2a\sqrt{1-a}\cdot\cfrac{1}{24}+2a\sqrt{1-a}\Big\{(-1+2-1)-\Big(-\cfrac{1}{8}+\cfrac{1}{2}-\cfrac{1}{2}\Big)\Big\}$
$=\cfrac{a}{12}\sqrt{1-a}+\cfrac{a}{4}\sqrt{1-a}$
$=\cfrac{a}{3}\sqrt{1-a}$
・・・ツテ
次に,$S^2$ を求めると
$S^2=\cfrac{a^2}{9}(1-a)=\cfrac{-1}{9}a^3+\cfrac{1}{9}a^2$
・・・トナニヌ
ここで,$g(x)=-\cfrac{1}{9}a^3+\cfrac{1}{9}a^2$ として,増減を調べる。
$-\cfrac{1}{9}a^3+\cfrac{1}{9}a^2=0$ とすると
$3a^2-2a=0$
$a(3a-2)=0$
$a=0$,$\cfrac{2}{3}$
$\def\arraystretch{1.25}\begin{array}{|c||c:c:c:c:c|}\hline a & \cdots & 0&\cdots&\frac{2}{3}&\cdots \\\hline g'(a) & – & 0&+&0&- \\\hline g(a) & \searrow & &\nearrow&\text{最大}&\searrow\\\hline\end{array}$
したがって,$S$ は $a=\cfrac{2}{3}$ で最大値をとる。
・・・ネノ
$g\Big(\cfrac{2}{3}\Big)=-\cfrac{1}{9}\Big(\cfrac{2}{3}\Big)^3+\cfrac{1}{9}\Big(\cfrac{2}{3}\Big)^2$
$=-\cfrac{2^3}{3^5}+\cfrac{2^2}{3^4}$
$=\cfrac{-2^3+2^2\cdot3}{3^5}$
$=\cfrac{-8+12}{3^5}=\cfrac{4}{3^5}$
よって
$S=\sqrt{\cfrac{4}{3^5}}=\cfrac{2}{9\sqrt{3}}=\cfrac{2\sqrt{3}}{27}$
・・・ハヒフヘ
[ad]
第2問 問題文
三角形 ABC の周の長さは 4 であり, AB = AC であるとする。BC = $2a\enspace (0\lt a\lt 1)$ とする。
(1) AB = $\boxed{\text{ア}}-\boxed{\text{イ}}$ である。このとき, 三角形 ABC の面積は $\boxed{\text{ウエ}}\sqrt{\boxed{\text{オ}}-a}$ である。
(2) 2 辺 AB, AC を $x:(1-x)$ $(0\lt x\lt1)$ に内分する点を, それぞれ P, Q とし, 直線 PQ に関して点 A と対称な点を R とする。三角形 RPQ の面積は
$(\boxed{\text{ウエ}}\sqrt{\boxed{\text{オ}}-a})x^{\boxed{\text{カ}}}\cdots\cdots$①
である。$0\lt x\lt1$ に対して, 三角形 RPQ と三角形 ABC の共通部分の面積を $f(x)$とおく。さらに, $f(0)=f(1)=0$ とおく。
$0\lt x\leqq\cfrac{1}{2}$ のとき, 点 R は三角形 ABC の内部または周上にある。したがって, $f(x)$ は ① に等しい。
$\cfrac{1}{2}\lt x\lt1$ のとき, 直線 PR, QR と直線 BC との交点をそれぞれ P’, Q’ とする。三角形 RP’Q’ と三角形 ABC は相似であり, その相似比は $(\boxed{\text{キ}}x-\boxed{\text{ク}}):1$ である。したがって
$f(x)=(\boxed{\text{ウエ}}\sqrt{\boxed{\text{オ}}-a})(\boxed{\text{ケコ}}x^{\boxed{\text{サ}}}+\boxed{\text{シ}}x-1)$
である。
$y=f(x)$ のグラフを調べることにより, $f(x)$ は $x=\cfrac{\boxed{\text{ス}}}{\boxed{\text{セ}}}$ のとき, 最大值 $\cfrac{\boxed{\text{ソタ}}}{\boxed{\text{チ}}}\sqrt{\boxed{\text{オ}}-a}$ をとることがわかる。
(3) 座標平面において, $y=f(x)$ のグラフと $x$ 軸で囲まれた図形の面積を $S$ とおくと
$S=\cfrac{\boxed{\text{ツ}}}{\boxed{\text{テ}}}\sqrt{\boxed{\text{オ}}-a}$
となる。$a$ が $0\lt a\lt 1$ の範囲を動くとき, $S$ の最大値を求めよう。
$S^2=\cfrac{\boxed{\text{トナ}}}{\boxed{\text{ニ}}}a^3+\cfrac{\boxed{\text{ヌ}}}{\boxed{\text{ニ}}}a^2$ である。$S^2$ の $0\lt a\lt1$ における増減を調べることにより, $S$ は $a=\cfrac{\boxed{\text{ネ}}}{\boxed{\text{ノ}}}$ のとき, 最大値 $\cfrac{\boxed{\text{ハ}}\sqrt{\boxed{\text{ヒ}}}}{\boxed{\text{フヘ}}}$ をとることがわかる。
SNSでシェア