【スマホで読む・わかりやすい】センター数学IIB2015追試【解説・正解・問題】

第4問　解答・解説

ア 3　イ,ウ 7,4　エ 2

オ 3　カ 0　キ,ク 1,4

ケ,コ,サ 5,3,4

シ,ス 3,4　セ,ソ 3,8

$\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos\angle\text{AOB}$

$=2\cdot3\cos 60\degree$

$=6\cdot\cfrac{1}{2}=3$

・・・ア

$(\vec{a}-\vec{p})(\vec{b}-\vec{p})=\cfrac{5}{4}$ の左辺を展開して

$\vec{a}\cdot\vec{b}-\vec{a}\cdot\vec{p}-\vec{b}\cdot\vec{p}+|\vec{p}|^2=\cfrac{5}{4}$

$|\vec{p}|^2-(\vec{a}+\vec{b})\cdot\vec{p}+\cfrac{7}{4}=0$

・・・イウ

式を平方完成すると

$\bigg|\vec{p}-\cfrac{\vec{a}+\vec{b}}{2}\bigg|^2-\cfrac{|\vec{a}+\vec{b}|^2}{4}+\cfrac{7}{4}=0$

ここで，$\vec{a}+\vec{b}$ を 2 乗すると

$(\vec{a}+\vec{b})^2=|\vec{a}|^2+2\vec{a}\cdot\vec{b}+|\vec{b}|^2$

$=4+2\cdot3+9=19$

よって

$\bigg|\vec{p}-\cfrac{\vec{a}+\vec{b}}{2}\bigg|^2-\cfrac{19}{4}+\cfrac{7}{4}=0$

$\bigg|\vec{p}-\cfrac{\vec{a}+\vec{b}}{2}\bigg|^2=3$

$\bigg|\vec{p}-\cfrac{\vec{a}+\vec{b}}{2}\bigg|=\sqrt{3}$

・・・エオ

次に，$\overrightarrow{\text{OC}}$ ⊥ $\overrightarrow{\text{MH}}$ より $\overrightarrow{\text{OC}}\cdot\overrightarrow{\text{MH}}=0$ を用いて

・・・カ

$\overrightarrow{\text{OC}}\cdot\overrightarrow{\text{MH}}=0$

$\overrightarrow{\text{OC}}\cdot(\overrightarrow{\text{OH}}-\overrightarrow{\text{OM}})=0$

$\overrightarrow{\text{OC}}\cdot\bigg(t\overrightarrow{\text{OC}}-\cfrac{\vec{a}+\vec{b}}{2}\bigg)=0$

$t|\overrightarrow{\text{OC}}|^2-\overrightarrow{\text{OC}}\cdot\cfrac{\vec{a}+\vec{b}}{2}=0$

$t=\overrightarrow{\text{OC}}\cdot\cfrac{\vec{a}+\vec{b}}{2}$

$=\cfrac{1}{2}(\vec{a}\cdot\overrightarrow{\text{OC}}+\vec{b}\cdot\overrightarrow{\text{OC}})$

$=\cfrac{1}{2}(|\vec{a}||\overrightarrow{\text{OC}}|\cos 120\degree+|\vec{b}||\overrightarrow{\text{OC}}|\cos60\degree)$

$=\cfrac{1}{2}\bigg\{2\cdot1\cdot\bigg(-\cfrac{1}{2}\bigg)+3\cdot1\cdot\cfrac{1}{2}\bigg\}$

$=\cfrac{1}{2}\bigg(-1+\cfrac{3}{2}\bigg)$

$=\cfrac{1}{4}$

・・・キク

また，$\overrightarrow{\text{MH}}=\overrightarrow{\text{OH}}-\overrightarrow{\text{OH}}$ に注意して

$|\overrightarrow{\text{MH}}|^2=\bigg(\cfrac{1}{4}\overrightarrow{\text{OC}}-\cfrac{\vec{a}+\vec{b}}{2}\bigg)^2$

$=\cfrac{1}{16}\{\overrightarrow{\text{OC}}-2(\vec{a}+\vec{b})\}^2$

$=\cfrac{1}{16}\{|\overrightarrow{\text{OC}}|^2-4(\vec{a}+\vec{b})\cdot\overrightarrow{\text{OC}}+4(\vec{a}+\vec{b})^2\}$

ここで，上で求めた $\overrightarrow{\text{OC}}\cdot\cfrac{\vec{a}+\vec{b}}{2}=\cfrac{1}{4}$ を利用して

$=\cfrac{1}{16}\bigg\{1-4\cdot\cfrac{1}{2}+4\cdot19\bigg\}$

$=\cfrac{75}{16}$

したがって

$|\overrightarrow{\text{MH}}|=\cfrac{\sqrt{75}}{4}=\cfrac{5\sqrt{3}}{4}$

・・・ケコサ

また，点 P と直線 OC の距離が最小になるのは，P が HM 上にあるときだから

$\cfrac{5\sqrt{3}}{4}-\sqrt{3}=\cfrac{\sqrt{3}}{4}$

・・・シス

△OCP の面積の最小値は OC を底辺，HP を高さとして考えれば

$\cfrac{1}{2}\cdot1\cdot\cfrac{\sqrt{3}}{4}=\cfrac{\sqrt{3}}{8}$

・・・セソ

第４問　問題文

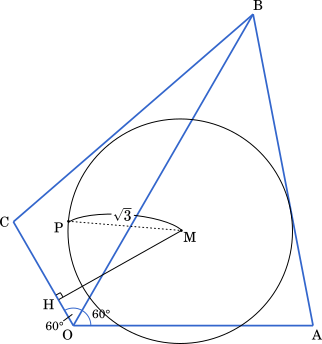
平面上の四角形 OABC において，$|\overrightarrow{\text{OA}}|=2$，$|\overrightarrow{\text{OB}}|=3$，$|\overrightarrow{\text{OC}}|=1$，∠AOB=∠BOC=$60\degree$ であるとする。点 P が

$\overrightarrow{\text{PA}}\cdot\overrightarrow{\text{PB}}=\cfrac{5}{4}\cdots$①

を満たしながら動くとき，三角形 OCP の面積の最小値を求めよう。以下，$\overrightarrow{\text{OA}}=\vec{a}$，$\overrightarrow{\text{OB}}=\vec{b}$，$\overrightarrow{\text{OP}}=\vec{p}$ とおく。

まず，点 P の動く範囲を考えよう。①は，$(\vec{a}-\vec{p})\cdot(\vec{b}-\vec{p})=\cfrac{5}{4}$ であるから，$\vec{a}\cdot\vec{b}=\boxed{\text{ ア }}$ に注意すると

$|\vec{p}|^2-(\vec{a}+\vec{b})\cdot\vec{p}+\cfrac{\boxed{\text{ イ }}}{\boxed{\text{ ウ }}}=0$

と書き換えられる。これはさらに

$\bigg|\vec{p}-\cfrac{\vec{a}+\vec{b}}{\boxed{\text{ エ }}}\bigg|=\sqrt{\boxed{\text{ オ }}}$

と書き換えられる。点 M を $\overrightarrow{\text{OM}}=\cfrac{\vec{a}+\vec{b}}{\boxed{\text{ エ }}}$ となるように定めると，点 P は，M を中心とする半径 $\sqrt{\boxed{\text{ オ }}}$ の円周上を動く。

次に，点 P と直線 OC の距離について考えよう。直線 OC 上の点 H を $\overrightarrow{\text{OC}}$⊥$\overrightarrow{\text{MH}}$ となるようにとる。実数 $t$ を用いて $\overrightarrow{\text{OH}}=t\overrightarrow{\text{OC}}$ と表すと，$\overrightarrow{\text{OC}}\cdot\overrightarrow{\text{MH}}=\boxed{\text{ カ }}$ であることから， $t=\cfrac{\boxed{\text{ キ }}}{\boxed{\text{ ク }}}$ となる。このとき，$|\overrightarrow{\text{MH}}|=\cfrac{\boxed{\text{ ケ}}\sqrt{\boxed{\text{ コ }}}}{\boxed{\text{ サ }}}$ であるから，点 P が①を満たしながら動くとき，点 P と直線 OC の距離の最小値は $\cfrac{\sqrt{\boxed{\text{ シ }}}}{\boxed{\text{ ス }}}$ となる。

したがって，三角形 OCP の面積の最小値は $\cfrac{\sqrt{\boxed{\text{ セ }}}}{\boxed{\text{ ソ }}}$ である。