【スマホで読む・わかりやすい】センター数学IIB2015追試【解説・正解・問題】

第2問　解答・解説

アイ,ウ,エ 2a,2,1　オ,カ 4,1

キ,ク 4,3　ケ 3　コ,サ 2,2

シ,ス 3,2　セ,ソ b,b

タチ,ツ －1,6　テ 2

ト,ナ 2,3　ニ,ヌ 5,2

ネ,ノ,ハ,ヒ 1,2,9,2

フ,ヘ 7,2

(1)

$y=1-x^2$

$y’=-2x$

$x=a$ のときの接線の傾きは $-2a$

これが，$(a,1-a^2)$ を通るので，$\ell$ の方程式は

$\ell:y-1+a^2=-2a(x-a)$

$y=-2ax+2a^2+1-a^2$

$=-2ax+a^2+1$

・・・アイウエ

また，直線 $\ell$ と原点 O の距離 $h$ は，点と直線の距離の公式 $d=\cfrac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}$ を用いるとよい。

$\ell:2ax+y-a^2-1=0$ と変形すると

$h=\cfrac{|2a\cdot0+0-a^2-1|}{\sqrt{(2a)^2+1^2}}$

$=\cfrac{a^2+1}{\sqrt{4a^2+1}}$

・・・オカ

ここで，$t=\sqrt{4a^2+1}$ とおくと

$t^2=4a^2+1$

$4a^2=t^2-1$

$a^2=\cfrac{t^2-1}{4}$

$a^2+1=\cfrac{t^2+3}{4}$

これを $h$ の式に代入すると

$h=\cfrac{\cfrac{t^2+3}{4}}{t}=\cfrac{1}{4}\bigg(\cfrac{t^2+3}{t}\bigg)$

$=\cfrac{1}{4}\bigg(t+\cfrac{3}{t}\bigg)$

・・・キク

また，$t$ と $\cfrac{3}{t}$ について，相加・相乗平均 $a+b\geqq2\sqrt{ab}$ を用いて

$t+\cfrac{3}{t}\geqq2\sqrt{t\cdot\cfrac{3}{t}}$

$t+\cfrac{3}{t}\geqq2\sqrt{3}$

相加・相乗平均の関係より，$t+\cfrac{3}{t}$ は $t=\cfrac{3}{t}$ のとき，最小値 $2\sqrt{3}$ をとる。

$t=\cfrac{3}{t}$

$t^2=3$

$4a^2+1=3$

$4a^2-2=0$

$2a^2-1=0$

$a^2-\cfrac{1}{2}=0$

$\bigg(a+\cfrac{\sqrt{2}}{2}\bigg)\bigg(a-\cfrac{\sqrt{2}}{2}\bigg)=0$

$a=\pm\cfrac{\sqrt{2}}{2}$

したがって，$h$ は $t^2=3$ のとき，つまり $a=\pm\cfrac{\sqrt{2}}{2}$ のとき，最小値 $h=\cfrac{1}{4}\cdot2\sqrt{3}=\cfrac{\sqrt{3}}{2}$ をとる。

・・・ケコサシス

(2)

直線 $m$ の傾きを求めると，傾きは $\cfrac{y \text{の変化量}}{x \text{の変化量}}$ だから

$\cfrac{2b-b^2-0}{1-b+1}=\cfrac{2b-b^2}{2-b}$

$=\cfrac{b(2-b)}{2-b}=b$

直線 $m$ は $(-1,0)$ を通るので

$m:y=b(x+1)=bx+b$

・・・セソ

次に，面積 $S_1$ を求めると，$\cfrac{1}{6}$ 公式 $S=\cfrac{|a|}{6}(\beta-\alpha)^3$ を用いて

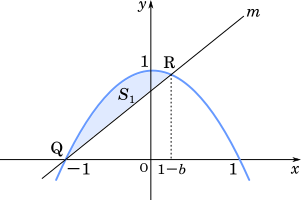
$S_1=\cfrac{1}{6}(1-b+1)^3$

$=\cfrac{1}{6}(2-b)^3$

$=\cfrac{1}{6}(8-12b+6b^2-b^3)$

$=\cfrac{-1}{6}b^3+b^2-2b+\cfrac{4}{3}$

・・・タチツテ

さらに，面積 $S_2$ を求めるには，台形の面積から図中の $T$ の面積を引くとよい。

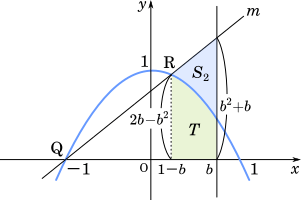
$x=b$ のとき

$m:y=b\cdot b+b=b^2+b$

台形の面積を求めると

$\cfrac{1}{2}(2b-b^2+b^2+b)\{b-(1-b)\}$

$=\cfrac{1}{2}\cdot3b(2b-1)$

$=3b^2-\cfrac{3}{2}b$

また，面積 $T$ は

$\displaystyle T=\int_{\small{1-b}}^{\small{b}}1-x^2dx$

$=\bigg[x-\cfrac{x^2}{3}\bigg]_{\small{1-b}}^{\small{b}}$

$=\bigg(b-\cfrac{b^3}{3}\bigg)-\bigg\{1-b-\cfrac{(1-b)^3}{3}\bigg\}$

$=2b-1+\cfrac{(1-b)^3-b^3}{3}$

$=2b-1+\cfrac{1-3b+3b^2-b^3-b^3}{3}$

$=2b-1+\cfrac{-2b^3+3b^2-3b+1}{3}$

$=-\cfrac{2}{3}b^3+b^2+b-\cfrac{2}{3}$

よって

$S_2=3b^2-\cfrac{3}{2}b+\cfrac{2}{3}b^3-b^2-b+\cfrac{2}{3}$

$=\cfrac{2}{3}b^3+2b^2-\cfrac{5}{2}b+\cfrac{2}{3}$

・・・トナニヌ

$S=S_1+S_2$ は

$S=\cfrac{1}{2}b^3+3b^2-\cfrac{9}{2}b+2$

・・・ネノハヒ

$S=f(b)$ として

$f'(b)=\cfrac{3}{2}b^2+6b-\cfrac{9}{2}$

$\cfrac{3}{2}b^2+6b-\cfrac{9}{2}=0$ とおくと

$3b^2+12b-9=0$

$b^2+4b-3=0$

$b=-2\pm\sqrt{4+3}$

$=-2\pm\sqrt{7}$

増減表をつくると

$\def\arraystretch{1.25}\begin{array}{|c||c|c|c|c|c|}\hline b&\cdots&-\sqrt{7}-2&\cdots&\sqrt{7}-2&\cdots\\\hline f'(b)&+&0&-&0&+\\\hline f(b)&\nearrow&&\searrow&\text{最小}&\nearrow\\\hline\end{array}$

したがって，$S$ は $b=\sqrt{7}-2$ で最小値をとる。

・・・フヘ

第２問　問題文

座標平面上の放物線 $y=1-x^2$ を $C$ とする。

(1)　放物線 $C$ 上の点 P$(a,1-a^2)$ における $C$ の接線を $\ell$ とする。$\ell$ の方程式は

$y=-\boxed{\text{ アイ }}x+a^{\boxed{\text{ウ}}}+\boxed{\text{ エ }}$

である。直線 $\ell$ と原点 O の距離 $h$ は

$h=\cfrac{a^{\boxed{\text{ウ}}+\boxed{\text{ エ }}}}{\sqrt{\boxed{\text{ オ }}\space a^2+\boxed{\text{ カ }}}}$

である。ここで，$t=\sqrt{\boxed{\text{ オ }}\space a^2+\boxed{\text{ カ }}}$ とおくと

$h=\cfrac{1}{\boxed{\text{ キ }}}\bigg(t+\cfrac{\boxed{\text{ ク }}}{t}\bigg)$

と表される。相加平均と相乗平均の関係により，$h$ は $t^2=\boxed{\text{ ケ }}$ のとき，つまり $a=\pm\cfrac{\sqrt{\boxed{\text{ コ }}}}{\boxed{\text{ サ }}}$ のとき，最小値 $\cfrac{\sqrt{\boxed{\text{ シ }}}}{\boxed{\text{ ス }}}$ をとることがわかる。

(2)　$\cfrac{1}{2} < b \leqq 1$ として，放物線 $C$ 上の 2 点 Q$(-1,0)$ と R$(1-b,2b-b^2)$ を通る直線を $m$ とする。$m$ の方程式は

$y=\boxed{\text{ セ }}\space x+\boxed{\text{ ソ }}$

である。

$C$ と直線 $m$ で囲まれた図形の面積 $S_1$ は

$S_1=\cfrac{\boxed{\text{ タチ }}}{\boxed{\text{ ツ }}}\space b^3+b^2-\boxed{\text{ テ }}\space b+\cfrac{4}{3}$

である。一方，$C$ と直線 $m$ の $1-b \leqq x \leqq b$ の部分，および直線 $x =b$ で囲まれた図形の面積 $S_2$ は

$S_2=\cfrac{\boxed{\text{ ト }}}{\boxed{\text{ ナ }}}b^3+2b^2-\cfrac{\boxed{\text{ ニ }}}{\boxed{\text{ ヌ }}}b+\cfrac{2}{3}$

である。よって，$S_1$ と $S_2$ の和 $S$ は

$S=S_1+S_2=\cfrac{\boxed{\text{ ネ }}}{\boxed{\text{ ノ }}}b^3+3b^2-\cfrac{\boxed{\text{ ハ }}}{\boxed{\text{ ヒ }}}b+2$

$\cfrac{1}{2} < b \leqq 1$ のとき，$S$ の増減を調べると，$S$ は $b=\sqrt{\boxed{\text{ フ }}}-\boxed{\text{ ヘ }}$ で最小値をとることがわかる。