【スマホで読む・わかりやすい】センター数学IIB2015本試【解説・正解・問題】

第4問　解答・解説

ア,イ,ウ 1,3,2　エ －　オ,カ 1,2

キ 0　ク,ケ 5,4　コ,サ 7,3

シス,セ 21,4　ソ,タ,チツ 7,3,24

テ,ト 7,9　ナ,ニ 1,3　ヌネ,ノハ －7,36

ヒ,フ 7,9　ヘホ 21

(1)

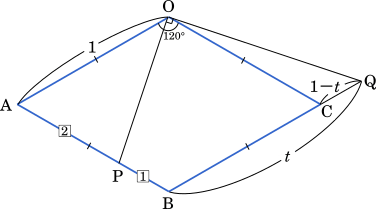
点 P は AB を 2 : 1 に内分する点だから

$\overrightarrow{\text{OP}}=\cfrac{\vec{a}+2\vec{b}}{3}=\cfrac{1}{3}\vec{a}+\cfrac{2}{3}\vec{b}$

・・・アイウ

また，$\overrightarrow{\text{OQ}}=(1-t)\overrightarrow{\text{OB}}+t\overrightarrow{\text{OC}}$ は

$\overrightarrow{\text{OC}}=\overrightarrow{\text{AB}}$ だから

$\overrightarrow{\text{AB}}=\overrightarrow{\text{OB}}-\overrightarrow{\text{OA}}=\vec{b}-\vec{a}$

よって

$\overrightarrow{\text{OQ}}=(1-t)\vec{b}+t(\vec{b}-\vec{a})$

$=\vec{b}-t\vec{b}+t\vec{b}-t\vec{a}$

$=-t\vec{a}+\vec{b}$

・・・エ

ここで

$\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos 60\degree$

$=1\cdot1\cdot\cfrac{1}{2}=\cfrac{1}{2}$

・・・オカ

また，$\overrightarrow{\text{OP}}$⊥$\overrightarrow{\text{OQ}}$ だから

$\overrightarrow{\text{OP}}\cdot\overrightarrow{\text{OQ}}=0$

・・・キ

$\overrightarrow{\text{OP}}\cdot\overrightarrow{\text{OQ}}=\bigg(\cfrac{1}{3}\vec{a}+\cfrac{2}{3}\vec{b}\bigg)(-t\vec{a}+\vec{b})=0$

$-\cfrac{1}{3}t|\vec{a}|^2+\cfrac{1}{3}\vec{a}\cdot\vec{b}-\cfrac{2}{3}t\vec{a}\cdot\vec{b}+\cfrac{2}{3}|\vec{b}|^2=0$

$-\cfrac{1}{3}t+\cfrac{1}{3}\cdot\cfrac{1}{2}-\cfrac{2}{3}\cdot\cfrac{1}{2}t+\cfrac{2}{3}=0$

$-\cfrac{2}{3}t+\cfrac{5}{6}=0$

$t=\cfrac{5}{4}$

・・・クケ

$|\overrightarrow{\text{OP}}|$ を求めると

$|\overrightarrow{\text{OP}}|^2=\bigg(\cfrac{1}{3}\vec{a}+\cfrac{2}{3}\vec{b}\bigg)^2$

$=\cfrac{1}{9}|\vec{a}|^2+\cfrac{4}{9}\vec{a}\cdot\vec{b}+\cfrac{4}{9}|\vec{b}|^2$

$=\cfrac{1}{9}+\cfrac{4}{9}\cdot\cfrac{1}{2}+\cfrac{4}{9}$

$=\cfrac{7}{9}$

したがって

$|\overrightarrow{\text{OP}}|=\cfrac{\sqrt{7}}{3}$

・・・コサ

また，$t=\cfrac{5}{4}$ を $\overrightarrow{\text{OQ}}=-t\vec{a}+\vec{b}$ に代入して

$\overrightarrow{\text{OQ}}=-\cfrac{5}{4}\vec{a}+\vec{b}$

$|\overrightarrow{\text{OQ}}|$ を求めると

$|\overrightarrow{\text{OQ}}|^2=\bigg(-\cfrac{5}{4}\vec{a}+\vec{b}\bigg)^2$

$=\cfrac{25}{16}|\vec{a}|^2-\cfrac{5}{2}\vec{a}\cdot\vec{b}+|\vec{b}|^2$

$\cfrac{25}{16}-\cfrac{5}{2}\cdot\cfrac{1}{2}+1$

$\cfrac{5}{16}+1$

$=\cfrac{21}{16}$

したがって

$|\overrightarrow{\text{OQ}}|=\cfrac{\sqrt{21}}{4}$

・・・シスセ

さらに，三角形 OPQ の面積 $S_1$ は，公式 $\cfrac{1}{2}bc\sin A$ を用いて

$S_1=\cfrac{1}{2}\cdot\cfrac{\sqrt{7}}{3}\cdot\cfrac{\sqrt{21}}{4}\sin\angle{\text{POQ}}$

∠POQ = 90° より $\sin$∠POQ = 1 だから

$S_1=\cfrac{7\sqrt{3}}{24}$

・・・ソタチツ

(2)

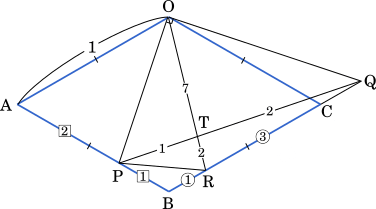
$\overrightarrow{\text{OT}}=r\overrightarrow{\text{OR}}=(1-2)\overrightarrow{\text{OP}}+s\overrightarrow{\text{OQ}}$

$\overrightarrow{\text{OR}}=\cfrac{3\overrightarrow{\text{OB}}+\overrightarrow{\text{OC}}}{1+3}=\cfrac{3}{4}\overrightarrow{\text{OB}}+\cfrac{1}{4}\overrightarrow{\text{OC}}$

$=\cfrac{3}{4}\vec{b}+\cfrac{1}{4}(\vec{b}-\vec{a})$

$=-\cfrac{1}{4}\vec{a}+\vec{b}$

よって

$r\overrightarrow{\text{OR}}=-\cfrac{1}{4}r\vec{a}+r\vec{b}$

また

$(1-s)\overrightarrow{\text{OP}}+s\overrightarrow{\text{OQ}}$

$=(1-s)\bigg(\cfrac{1}{3}\vec{a}+\cfrac{2}{3}\vec{b}\bigg)+s\bigg(-\cfrac{5}{4}\vec{a}+\vec{b}\bigg)$

$=\cfrac{1}{3}\vec{a}+\cfrac{2}{3}\vec{b}-\cfrac{1}{3}s\vec{a}-\cfrac{2}{3}s\vec{b}-\cfrac{5}{4}s\vec{a}+s\vec{b}$

$=\bigg(\cfrac{1}{3}-\cfrac{19}{12}s\bigg)\vec{a}+\bigg(\cfrac{2}{3}+\cfrac{1}{3}s\bigg)\vec{b}$

式を比べると

$\begin{cases}-\cfrac{1}{4}r=\cfrac{1}{3}-\cfrac{19}{12}s\\r=\cfrac{2}{3}+\cfrac{1}{3}s\end{cases}$

式を整理すると

$-\cfrac{1}{4}r=\cfrac{1}{3}-\cfrac{19}{12}s$

$3r=19s-4$

また

$r=\cfrac{2}{3}+\cfrac{1}{3}s$

$3r=s+2$

よって

$19s-4=s+2$

$s=\cfrac{1}{3}$

・・・ナニ

これより，PT : TQ = 1 : 2 であることが分かる。

また，$s=\cfrac{1}{3}$ を $3r=s+2$ に代入すると

$3r=\cfrac{1}{3}+2=\cfrac{7}{3}$

$r=\cfrac{7}{9}$

・・・テト

これより，OT : TR = 7 : 2 であることが分かる。

次に，$\overrightarrow{\text{OT}}$ を求めると，$\overrightarrow{\text{OT}}=-\cfrac{1}{4}r\vec{a}+r\vec{b}$ より

$\overrightarrow{\text{OT}}=-\cfrac{1}{4}\cdot\cfrac{7}{9}\vec{a}+\cfrac{7}{9}\vec{b}$

$=-\cfrac{-7}{36}\vec{a}+\cfrac{7}{9}\vec{b}$

・・・ヌネノハヒフ

また

△OPT = $\cfrac{1}{3}S_1$

$S_2=\cfrac{2}{7}\times$△OPT

であるから

$S_2=\cfrac{2}{7}\cdot\cfrac{1}{3}S_1=\cfrac{2}{21}S_1$

$\cfrac{S_1}{S_2}=\cfrac{21}{2}$

したがって

$S_1:S_2=21:2$

・・・ヘホ

第４問　問題文

1 辺の長さが $1$ のひし形 OABC において，∠AOC=$120\degree$ とする。辺 AB を $2:1$ に内分する点を P とし，直線 BC 上に点 Q を $\overrightarrow{\text{OP}}$⊥$\overrightarrow{\text{OQ}}$ となるようにとる。以下，$\overrightarrow{\text{OA}}=\vec{a}$，$\overrightarrow{\text{OB}}=\vec{b}$ とおく。

(1)　三角形 OPQ の面積を求めよう。$\overrightarrow{\text{OP}}=\cfrac{\boxed{\text{ ア }}}{\boxed{\text{ イ }}}\vec{a}+\cfrac{\boxed{\text{ ウ }}}{\boxed{\text{ イ }}}\vec{b}$ である。実数 $t$ を用いて $\overrightarrow{\text{OQ}}=(1-t)\overrightarrow{\text{OB}}+t\overrightarrow{\text{OC}}$ と表されるので， $\overrightarrow{\text{OQ}}=\boxed{\text{ エ }}t\vec{a}+\vec{b}$ である。ここで，$\vec{a}\cdot\vec{b}=\cfrac{\boxed{\text{ オ }}}{\boxed{\text{ カ }}}$，$\overrightarrow{\text{OP}}\cdot\overrightarrow{\text{OQ}}=\boxed{\text{ キ }}$ であることから，$t=\cfrac{\boxed{\text{ ク }}}{\boxed{\text{ ケ }}}$ である。

これらのことから，$|\overrightarrow{\text{OP}}|=\cfrac{\sqrt{\boxed{\text{ コ }}}}{\boxed{\text{ サ }}}$，$|\overrightarrow{\text{OQ}}|=\cfrac{\sqrt{\boxed{\text{ シス }}}}{\boxed{\text{ セ }}}$ である。よって，三角形 OPQ の面積 $S_1$ は，$S_1=\cfrac{\boxed{\text{ ソ }}\sqrt{\boxed{\text{ タ }}}}{\boxed{\text{ チツ }}}$ である。

(2)　辺 BC を $1:3$ に内分する点を R とし，直線 OR と直線 PQ との交点を T とする。$\overrightarrow{\text{OT}}$ を $\vec{a}$ と $\vec{b}$ を用いて表し，三角形 OPQ と三角形 PRT の面積比を求めよう。

T は直線 OR 上の点であり，直線 PQ 上の点でもあるので，実数 $r$，$s$ を用いて

$\overrightarrow{\text{OT}}=r \overrightarrow{\text{OR}}=(1-s)\overrightarrow{\text{OP}}+s\overrightarrow{\text{OQ}}$

と表すと，$r=\cfrac{\boxed{\text{ テ }}}{\boxed{\text{ ト }}}$，$s=\cfrac{\boxed{\text{ ナ }}}{\boxed{\text{ ニ }}}$ となることがわかる。よって，

$\overrightarrow{\text{OT}}=\cfrac{\boxed{\text{ ヌネ }}}{\boxed{\text{ ノハ }}}\vec{a}+\cfrac{\boxed{\text{ ヒ }}}{\boxed{\text{ フ }}}\vec{b}$ である。

上で求めた $r$，$s$ の値から，三角形 OPQ の面積 $S_1$ と，三角形 PRT の面積 $S_2$ との比は，$S_1:S_2=\boxed{\text{ ヘホ }}:2$ である。