【スマホで読む・わかりやすい】センター数学IIB2015本試【解説・正解・問題】

第2問　解答・解説

ア,イ a,2　ウ 0　エ a　オ,カ a,2

キ,ク a,2　ケコ,サ,シ,ス －1,a,1,2

セ,ソ 1,8　タ,チツ 3,12

テ,トナ 3,24　ニ 3　ヌ 1

ネノ,ハヒ －1,12

(1)

平均変化率は $\cfrac{y\text{の変化量}}{x\text{の変化量}}$ である。$x$ が $a$ から $a+h$ まで変化するとき，$y$ は $\cfrac{1}{2}a^2$ から $\cfrac{1}{2}(a+h)^2$ まで変化するので

$\cfrac{\cfrac{1}{2}(a+h)^2-\cfrac{1}{2}a^2}{(a+h)-a}$

となる。

$=\cfrac{a2+2ah+h^2-a^2}{2h}$

$=\cfrac{2a+h}{2}$

$=a+\cfrac{h}{2}$

・・・アイ

したがって，微分係数は

$\displaystyle f'(a)=\lim_{h\rightarrow0}\bigg(a+\cfrac{h}{2}\bigg)=a$

・・・ウエ

(2)

$y=\cfrac{1}{2}x^2$

$y’=x$

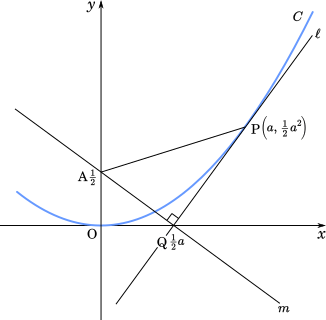
よって，$x=a$ のとき，接線の傾きは $a$ である。したがって，接線 $\ell$ の方程式は

$\ell:y-\cfrac{1}{2}a^2=a(x-a)$

$y=a(x-a)+\cfrac{1}{2}a^2$

$=ax-a^2+\cfrac{1}{2}a^2$

$=ax-\cfrac{1}{2}a^2$

・・・オカ

また，交点 Q の座標を求めると， $y=0$ を代入して

$0=ax-\cfrac{1}{2}a^2$

$ax=\cfrac{1}{2}a^2$

$x=\cfrac{a}{2}$

したがって，交点 Q の座標は $\bigg(\cfrac{a}{2},\enspace0\bigg)$

・・・キク

次に，直線 $m$ の傾きを $k$ とすると

$ak=-1$

$k=-\cfrac{1}{a}$

したがって，$m$ の方程式は

$m:y=-\cfrac{1}{a}\bigg(x-\cfrac{a}{2}\bigg)$

$=\cfrac{-1}{a}x+\cfrac{1}{2}$

・・・ケコサシス

面積 $S$ を求める。まず，点 A の座標を求めると，点 A は直線 $m$ と $y$ 軸との交点だから，$y$ 座標は切片の $\cfrac{1}{2}$ である。よって，点 A の座標は $\bigg(0,\cfrac{1}{2}\bigg)$

△APQ が直角三角形になることに注意して，三平方の定理を用いて底辺と高さを求めると

$\text{PQ}=\sqrt{\bigg(a-\cfrac{a}{2}\bigg)^2+\bigg(\cfrac{1}{2}a^2\bigg)^2}$

$=\sqrt{\cfrac{a^2+a^4}{4}}$

$=\cfrac{a}{2}\sqrt{a^2+1}$

$\text{AQ}=\sqrt{\bigg(\cfrac{a}{2}\bigg)^2+\bigg(\cfrac{1}{2}\bigg)^2}$

$=\sqrt{\cfrac{a^2+1}{4}}$

$=\cfrac{1}{2}\sqrt{a^2+1}$

よって

$S=\cfrac{1}{2}\cdot\cfrac{a}{2}\sqrt{a^2+1}\cdot\cfrac{1}{2}\sqrt{a^2+1}$

$=\cfrac{a(a^2+1)}{8}$

・・・セソ

次に，面積 $T$ を求める。点 P から $x$ 軸に垂線を下ろし，$x$ 軸と交わる点を H とする。面積 $T$ は台形 OAPH から曲線 OP，直線 PH，$x$ 軸で囲まれた図形の面積を引けば求められる。

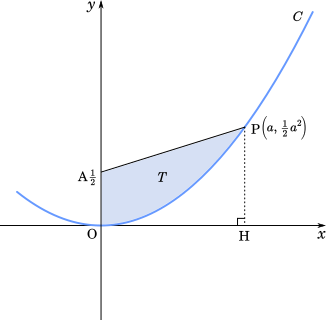
台形 OAPH の面積は

$\cfrac{1}{2}\bigg(\cfrac{1}{2}+\cfrac{1}{2}a^2\bigg)a=\cfrac{a^3+a}{4}$

$\displaystyle T=\cfrac{a^3+a}{4}-\int_0^a \cfrac{1}{2}x^2 dx$

$=\cfrac{a^3+a}{4}-\bigg[\cfrac{x^3}{6}\bigg]_0^a$

$=\cfrac{a3+a}{4}-\cfrac{a^3}{6}$

$=\cfrac{3a^3+3a-2a^3}{12}$

$=\cfrac{a(a^2+3)}{12}$

・・・タチツ

また

$S-T=\cfrac{a(a^2+1)}{8}-\cfrac{a(a^2+3)}{12}$

$=\cfrac{3a(a^2+1)-2a(a^2+3)}{24}$

$=\cfrac{3a^3+3a-2a^3-6a}{24}$

$=\cfrac{a^3-3a}{24}$

$=\cfrac{a(a^2-3)}{24}$

・・・テトナ

$S-T\gt0$ となるような $a$ のとり得る値の範囲は

$\cfrac{a(a^2-3)}{24}\gt0$

$a(a^2-3)\gt0$

$a\gt0$ だから，正の数×正の数 $\gt0$ とすれば不等式が成り立つ。よって

$a^2-3\gt0$

$a^2\gt3$

$a\gt\sqrt{3}$

・・・ニ

$S-T$ の増減を調べると，$g(a)=\cfrac{a(a^2-3)}{24}$ とおいて

$g(a)=\cfrac{1}{24}a^3-\cfrac{1}{8}a$

$g'(a)=\cfrac{1}{8}a^2-\cfrac{1}{8}$

$=\cfrac{1}{8}(a^2-1)$

ここで，$\cfrac{1}{8}(a^2-1)=0$ とすると

$a^2-1=0$

$(a+1)(a-1)=0$

$a=1,-1$

$a\gt0$ より，$a=1$

増減表をつくると

$\def\arraystretch{1.2}\begin{array}{|c||c|c|c|}\hline a & \cdots & 1 &\cdots \\ \hline g'(a) & – & 0&+ \\\hline g(a) & \searrow & \cfrac{-1}{12} & \nearrow\\\hline\end{array}$

$g(1)=\cfrac{1(1^2-3)}{24}=\cfrac{-1}{24}$

したがって，$S-T$ は $a=1$ で最小値 $\cfrac{-1}{24}$ をとる。

・・・ヌネノハヒ

第２問　問題文

(1)　関数 $f(x)=\cfrac{1}{2}x^2$ の $x=a$ における微分係数 $f′(a)$ を求めよう。$h$ が $0$ でないとき，$x$ が $a$ から $a+h$ まで変化するときの $f(x)$ の平均変化率は $\boxed{\text{ ア }}+\cfrac{h}{\boxed{\text{ イ }}}$ である。したがって，求める微分係数は

$\displaystyle f′(a)=\lim_{h\rightarrow\boxed{\text{ウ}}}\bigg(\boxed{\text{ ア }}+\cfrac{h}{\boxed{\text{ イ }}}\bigg)=\boxed{\text{ エ }}$

である。

(2)　放物線 $y=\cfrac{1}{2}x^2$ を $C$ とし，$C$ 上に点 P$\bigg(a,\cfrac{1}{2}a^2\bigg)$ をとる。ただし，$a\gt0$ とする。点 P における $C$ の接線 $\ell$ の方程式は

$y=\boxed{\text{ オ }}x-\cfrac{1}{\boxed{\text{ カ }}}a^2$

である。直線 $\ell$ と $x$ 軸との交点 Q の座標は $\bigg(\cfrac{\boxed{\text{ キ }}}{\boxed{\text{ ク }}},0\bigg)$ である。点 Q を通り $\ell$ に垂直な直線を $m$ とすると，$m$ の方程式は

$y=\cfrac{\boxed{\text{ ケコ }}}{\boxed{\text{ サ }}}x+\cfrac{\boxed{\text{ シ }}}{\boxed{\text{ ス }}}$

である。

直線 $m$ と $y$ 軸との交点を A とする。三角形 APQ の面積を $S$ とおくと

$S=\cfrac{a(a^2+\boxed{\text{ セ }})}{\boxed{\text{ ソ }}}$

となる。また，$y$ 軸と線分 AP および曲線 $C$ によって囲まれた図形の面積を $T$ とおくと

$T=\cfrac{a(a^2+\boxed{\text{ タ }})}{\boxed{\text{ チツ }}}$

となる。

$a\gt0$ の範囲における $S-T$ の値について調べよう。

$S-T=\cfrac{a(a^2-\boxed{\text{ テ }})}{\boxed{\text{ トナ }}}$

である。$a\gt0$ であるから，$S-T\gt0$ となるような $a$ のとり得る値の範囲は $a\gt\sqrt{\boxed{\text{ ニ }}}$ である。また，$a\gt0$ のときの $S-T$ の増減を調べると，$S-T$ は $a=\boxed{\text{ ヌ }}$ で最小値 $\cfrac{\boxed{\text{ ネノ }}}{\boxed{\text{ ハヒ }}}$ をとることがわかる。