【スマホで読む・わかりやすい】センター数学IIB2015本試【解説・正解・問題】

第1問　解答・解説

ア 2　イ 1　ウ 5　エ 4　オ 6

カ,キ 4,5　ク 3　ケ 6　コ 3

サ,シ 2,9　ス,セソ 2,－3

タ,チツ,テ 2,－2,3　トナ －2

ニ 2　ヌ 2　ネノ,ハ －5,4

〔1〕

(1)

三平方の定理を用いて

$\text{OP}^2=(2\cos\theta)^2+(2\sin\theta)^2$

$=4(\sin^2\theta+\cos^2\theta)$

$=4$

したがって

$\text{OP}=2$

・・・ア

また

$\text{PQ}^2=(2\cos\theta+\cos7\theta-2\cos\theta)^2+(2\sin\theta+\sin7\theta-2\sin\theta)^2$

$=\cos^2 7\theta+\sin^2 7\theta$

$=1$

したがって

$\text{PQ}=1$

・・・イ

次に OQ を求めると

$\text{OQ}^2=(2\cos\theta+\cos7\theta)^2+(2\sin\theta+\sin7\theta)^2$

$=4\cos^2\theta+4\cos\theta\cos7\theta+\cos^2 7\theta+4\sin^2\theta+4\sin\theta\cos7\theta+\sin^2 7\theta$

$=4(\sin^2\theta+\cos^2\theta)+4(\cos7\theta\cos\theta+\sin7\theta\sin\theta)+\sin^2 7\theta+\cos^2 7\theta$

$=5+4(\cos7\theta\cos\theta+\sin7\theta\sin\theta)$

・・・ウエ

ここで，加法定理を用いて

$=5+4\cos (7\theta-\theta)$

$=5+4\cos(6\theta)$

・・・オ

$\cfrac{\pi}{8}\leqq\theta\leqq\cfrac{\pi}{4}$ の範囲で考えると

$\cfrac{\pi}{8}\leqq\theta\leqq\cfrac{\pi}{4}$

$\cfrac{3}{4}\pi\leqq6\theta\leqq\cfrac{3}{2}\pi$

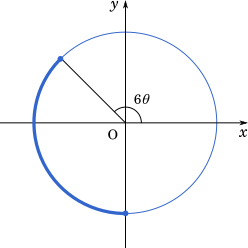
$\cos6\theta$ は，$6\theta=\cfrac{3}{2}\pi$ つまり $\theta=\cfrac{\pi}{4}$ で最大値 $0$ をとる。

・・・カ

これを代入して

$\text{OQ}^2=5+4\cdot0=5$

$\text{OQ}=\sqrt{5}$

・・・キ

(2)

直線 OP の傾きは 傾き = $\cfrac{y\text{の変化量}}{xの変化量}$ を用いて

$y=\cfrac{2\sin\theta}{2\cos\theta}\space x$

と表せる。これを変形して

$(\sin\theta)x-(\cos\theta)y=0$

・・・ク

これが点 Q を通るので，$x,y$ に点 Q の座標を代入すると

$\sin\theta(2\cos\theta+\cos7\theta)-\cos\theta(2\sin\theta+\sin7\theta)=0$

$2\sin\theta\cos\theta+\sin\theta\cos7\theta-2\sin\theta\cos\theta-\cos\theta\sin7\theta=0$

$\sin\theta\cos7\theta-\cos\theta\sin7\theta=0$

加法定理を用いて

$\sin(\theta-7\theta)=0$

$\sin(-6\theta)=0$

$-6\theta=0,\pi$

$\theta=0,\cfrac{\pi}{6}$

このうち，$\cfrac{\pi}{8}\leqq\theta\leqq\cfrac{\pi}{4}$ の範囲に当てはまるものは $\theta=\cfrac{\pi}{6}$

・・・ケ

(3)

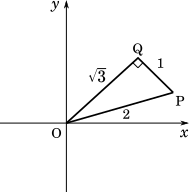
図より，△OQP は 辺の比がそれぞれ $1:2:\sqrt{3}$ の直角三角形であることが分かる。したがって，∠OQP が直角になるのは OQ = $\sqrt{3}$ のとき。

・・・コ

これを代入して

$\text{OP}^2=5+4\cos6\theta$

$3=5+4\cos6\theta$

$\cos6\theta=-\cfrac{1}{2}$

$6\theta=\cfrac{2}{3}\pi,\cfrac{4}{3}\pi$

$\theta=\cfrac{1}{9}\pi,\cfrac{2}{9}\pi$

このうち，$\cfrac{\pi}{8}\leqq\theta\leqq\cfrac{\pi}{4}$ の範囲に当てはまるものは $\theta=\cfrac{2}{9}\pi$

・・・サシ

〔2〕

(1)

$x\sqrt{y^3}=a$ の両辺を 2 乗して

$x^2y^3=a^2$

また，$\sqrt[3]{x}y=b$ の両辺を 3 乗して

$xy^3=b^3$

$y^3=b^3x^{-1}$

これを $x^2y^3=a^2$ に代入して

$x^2b^3x^{-1}=a^2$

$x=a^2b^{-3}$

これを $y^3=b^3x^{-1}$ に代入して

$y^3=b^3(a^2b^{-3})^{-1}$

$=b^3a^{-2}b^3=a^{-2}b^6$

$y=a^{\small-\frac{2}{3}}b^2$

したがって，$p=-\cfrac{2}{3}$ とすると

$x=a^2b^{-3},\enspace y=a^pb^2$

・・・スセソタチツ

(2)

$b=2\sqrt[3]{a^4}=2a^{\small\frac{4}{3}}$ として，$x,y$ に代入すると

$x=a^2(2a^{\small\frac{4}{3}})^{-3}$

$=a^2\cdot2^{-3}a^{-4}$

$=2^{-3}a^{-2}$

・・・トナ

$y=a^{\small-\frac{2}{3}}(2a^{\small\frac{4}{3}})^2$

$=a^{\small-\frac{2}{3}}\cdot2^2a^{\small\frac{8}{3}}$

$=2^2a^2$

・・・ニ

相加・相乗平均より

$x+y\geqq2\sqrt{xy}$

$\geqq2\sqrt{2^{-3}a^{-2}\cdot2^2a^2}$

$\geqq2\sqrt{2^{-1}}$

$\geqq2\sqrt{\cfrac{1}{2}}$

$\geqq\cfrac{2}{\sqrt{2}}$

$\geqq\sqrt{2}$

したがって，最小値は $\sqrt{2}$

・・・ヌ

また，相加・相乗平均において，等号が成り立つのは $x=y$ のときだから

$2^{-3}a^{-2}=2^2a^2$

$a^2\div a^{-2}=2^{-3}\div 2^2$

$a^{2-(-2)}=2^{-3-2}$

$a^4=2^{-5}$

$a=2^{\small-\frac{5}{4}}$

よって，$q=\cfrac{-5}{4}$

第１問，第２問は必答。第３問～第５問はいずれか２問を選択し，解答する。第５問は省略。

第１問　問題文

〔1〕　O を原点とする座標平面上の 2 点 P$(2\cos\theta,2\sin\theta)$，Q$(2\cos\theta+\cos 7\theta,2\sin\theta+\sin 7\theta)$ を考える。ただし，$\cfrac{\pi}{8}\leqq\theta\leqq\cfrac{\pi}{4}$ とする。

(1)　OP=$\boxed{\text{ ア }}$，PQ=$\boxed{\text{ イ }}$ である。また

$\text{OQ}^2=\boxed{\text{ ウ }}+\boxed{\text{ エ }}(\cos 7\theta\space\cos\theta+\sin 7\theta\sin\theta)$

$=\boxed{\text{ ウ }}+\boxed{\text{ エ }}\cos(\boxed{\text{ オ }}\theta)$

である。

よって，$\cfrac{\pi}{8}\leqq\theta\leqq\cfrac{\pi}{4}$ の範囲で， OQ は $\theta=\cfrac{\pi}{\boxed{\text{ カ }}}$ のとき最大値 $\sqrt{\boxed{ \text{ キ }}}$ をとる。

(2)　3 点 O，P，Q が一直線上にあるような $\theta$ の値を求めよう。

直線 OP を表す方程式は $\boxed{\text{ ク }}$ である。$\boxed{\text{ ク }}$ に当てはまるものを，次の⓪～③のうちから一つ選べ。

⓪ $(\cos\theta)x+(\sin\theta)y=0$

① $(\sin\theta)x+(\cos\theta)y=0$

② $(\cos\theta)x-(\sin\theta)y=0$

③ $(\sin\theta)x-(\cos\theta)y=0$

このことにより，$\cfrac{\pi}{8}\leqq\theta\leqq\cfrac{\pi}{4}$ の範囲で，3 点 O，P，Q が一直線上にあるのは $\theta=\cfrac{\pi}{\boxed{\text{ ケ }}}$ のときであることがわかる。

(3)　∠OQP が直角となるのは OQ=$\boxed{\text{ コ }}$ のときである。したがって $\cfrac{\pi}{8}\leqq\theta\leqq\cfrac{\pi}{4}$ の範囲で，∠OQP が直角となるのは $\theta=\cfrac{\boxed{\text{ サ }}}{\boxed{\text{ シ }}}\pi$ のときである。

〔2〕　$a$，$b$ を正の実数とする。連立方程式

$(＊)\begin{cases}x\sqrt{y^3}=a\\\sqrt[3]{x}\space y=b\end{cases}$

を満たす正の実数 $x$，$y$ について考えよう。

(1)　連立方程式(＊)を満たす正の実数 $x$，$y$ は

$x=a^{\boxed{\text{ス}}}b^{\boxed{\text{セソ}}}$，$y=a^p b^{\boxed{\text{タ}}}$

となる。ただし

$p=\cfrac{\boxed{\text{ チツ }}}{\boxed{\text{ テ }}}$

である。

(2)　$b=2\sqrt[3]{a^4}$ とする。$a$ が $a\gt0$ の範囲を動くとき，連立方程式(＊)を満たす正の実数 $x$，$y$ について，$x+y$ の最小値を求めよう。

$b=2\sqrt[3]{a^4}$ であるから，(＊)を満たす正の実数 $x$，$y$ は，$a$ を用いて

$x=2^{\boxed{\text{セソ}}}a^{\boxed{\text{トナ}}}$，$y=2^{\boxed{\text{タ}}}a^{\boxed{\text{ニ}}}$

と表される。したがって，相加平均と相乗平均の関係を利用すると，$x+y$ は $a =2^q$ のとき最小値 $\sqrt{\boxed{\text{ ヌ }}}$ をとることがわかる。ただし

$q=\cfrac{\boxed{\text{ ネノ }}}{\boxed{\text{ ハ }}}$

である。