【スマホで読む・わかりやすい】センター数学IIB2014追試【解説・正解・問題】

第４問

平面上に，1 辺の長さが $1$ の正方形 ABCD と，その外側に三角形 OAB があり，OA=OB=$\cfrac{\sqrt{5}}{2}$ とする。$0 < t < 1$ とし，線分 OA，AD，CB を $t:(1-t)$ に内分する点をそれぞれ P，Q，R とする。以下では，$\overrightarrow{\text{OA}}=\vec{a}$，$\overrightarrow{\text{OB}}=\vec{b}$ とおく。

(1)　$|\vec{a}-\vec{b}|^2=\boxed{\text{ ア }}$ により，$\vec{a}\cdot\vec{b}=\cfrac{\boxed{\text{ イ }}}{\boxed{\text{ ウ }}}$ である。また，$\vec{a}+\vec{b}$ と $\overrightarrow{\text{AD}}$ は平行であり，$|\vec{a}+\vec{b}|=\boxed{\text{ エ }}$ により，$\overrightarrow{\text{AD}}=\cfrac{\boxed{\text{ オ }}}{\boxed{\text{ カ }}}(\vec{a}+\vec{b})$ である。

次に，$\overrightarrow{\text{PQ}}$，$\overrightarrow{\text{PR}}$ を $t$ と $\vec{a}$，$\vec{b}$ を用いて表すと

$\overrightarrow{\text{PQ}}=\cfrac{\boxed{\text{ キ }}-t}{\boxed{\text{ ク }}}\vec{a}+\cfrac{t}{\boxed{\text{ ク }}}\vec{b}\cdots$①

$\overrightarrow{\text{PR}}=\cfrac{1-\boxed{\text{ ケ }}t}{\boxed{\text{ ク }}}\vec{a}+\cfrac{\boxed{\text{ コ }}-t}{\boxed{\text{ ク }}}\vec{b}\cdots$②

である。

(2)　$0 < t < 1$ の範囲において，三角形 PQR の面積 $S$ の最小値を求めよう。点 P から線分 CD に引いた垂線と線分 QR の交点を T とする。三角形 PTQ と三角形 PTR の面積の和は $S$ に等しいから，$S=\cfrac{\boxed{\text{ サ }}}{\boxed{\text{ シ }}}$PT である。これにより， PT が最小になるときを考えればよいことがわかる。

まず，QT:TR=$(1-t):\boxed{\text{ ス }}$ であるから

$\overrightarrow{\text{PT}}=\boxed{\text{ セ }}\overrightarrow{\text{PQ}}+\boxed{\text{ ソ }}\overrightarrow{\text{PR}}\cdots$③
である。$\boxed{\text{ ス }}$，$\boxed{\text{ セ }}$，$\boxed{\text{ ソ }}$ に当てはまるものを，次の⓪～⑦のうちから一つずつ選べ。ただし，同じものを繰り返し選んでもよい。

⓪ $t$　① $(1-t)$

② $(1+t)$　③ $(1+2t)$

④ $\cfrac{t}{2}$　⑤ $\cfrac{1-t}{2}$

⑥ $\cfrac{1+t}{2}$　⑦ $\cfrac{1+2t}{2}$

したがって，①，②，③ により

$\overrightarrow{\text{PT}}=\bigg(\cfrac{\boxed{\text{ タ }}}{\boxed{\text{ チ }}}t^2-\cfrac{\boxed{\text{ ツ }}}{\boxed{\text{ テ }}}t+\cfrac{3}{4}\bigg)(\vec{a}+\vec{b})$

となる。よって，$t=\cfrac{\boxed{\text{ ト }}}{\boxed{\text{ ナ }}}$ のとき， PT は最小になり，三角形 PQR の面積 $S$ の最小値は $\cfrac{\boxed{\text{ ニヌ }}}{\boxed{\text{ ネノ }}}$ である。

[ad]

解答・解説

ア 1　イ,ウ 3,4　エ 2

オ,カ 1,2　キ,ク 2,2　ケ,コ 3,3

サ,シ 1,2　ス 2　セ,ソ 6,5

タ,チ,ツ,テ 1,2,3,4

ト,ナ 3,4　ニヌ,ネノ 15,32

(1)

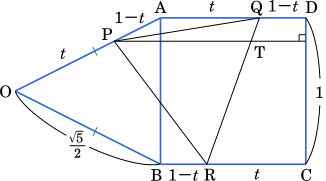
$|\vec{a}-\vec{b}|^2=|\overrightarrow{\text{BA}}|^2=1$

また $|\vec{a}-\vec{b}|^2$ を展開すると

$|\vec{a}-\vec{b}|^2=|\vec{a}|^2-2\vec{a}\cdot\vec{b}+|\vec{b}|^2=1$

$\bigg(\cfrac{\sqrt{5}}{2}\bigg)^2-2\vec{a}\cdot\vec{b}+\bigg(\cfrac{\sqrt{5}}{2}\bigg)^2=1$

$\cfrac{5}{4}-2\vec{a}\cdot\vec{b}+\cfrac{5}{4}=1$

$2\vec{a}\cdot\vec{b}=\cfrac{3}{2}$

$\vec{a}\cdot\vec{b}=\cfrac{3}{4}$

また，三平方の定理を用いて

$\sqrt{\bigg(\cfrac{\sqrt{5}}{2}\bigg)^2-\bigg(\cfrac{1}{2}\bigg)^2}=1$

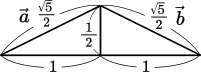
したがって，$|\vec{a}+\vec{b}|=2$

また，$\vec{a}+\vec{b}$ と $\overrightarrow{\text{AD}}$ は平行かつ $|\overrightarrow{\text{AD}}|=1$ だから

$\overrightarrow{\text{AD}}=\cfrac{1}{2}(\vec{a}+\vec{b})$

次に，

$\overrightarrow{\text{PQ}}=\overrightarrow{\text{OQ}}-\overrightarrow{\text{OP}}$

ここで，$\overrightarrow{\text{OQ}}=\overrightarrow{\text{OA}}+\overrightarrow{\text{AQ}}$ だから

$=\vec{a}+t\overrightarrow{\text{AD}}-t\vec{a}$

$=\vec{a}+\cfrac{t}{2}(\vec{a}+\vec{b})-t\vec{a}$

$=\cfrac{2-t}{2}\vec{a}+\cfrac{t}{2}\vec{b}\cdots\cdots$①

また

$\overrightarrow{\text{PR}}=\overrightarrow{\text{OR}}-\overrightarrow{\text{OP}}$

ここで，$\overrightarrow{\text{OR}}=\overrightarrow{\text{OB}}+\overrightarrow{\text{BR}}$ だから

$=\vec{b}+(1-t)\overrightarrow{\text{BC}}-t\vec{a}$

$\overrightarrow{\text{BC}}=\overrightarrow{\text{AD}}$ より

$=\vec{b}+(1-t)\cdot\cfrac{1}{2}(\vec{a}+\vec{b})-t\vec{a}$

$=\vec{b}+\cfrac{1-t}{2}\vec{a}+\cfrac{1-t}{2}\vec{b}-t\vec{a}$

$=\cfrac{1-3t}{2}\vec{a}+\cfrac{3-t}{2}\vec{b}\cdots\cdots$②

(2)

三角形の底辺を PT として，△PTQ の高さを $h$ とすると，△PTR の高さは $1-h$ となる。よって

$S=\cfrac{1}{2}\space\text{PT}\cdot h+\cfrac{1}{2}\space\text{PT}\cdot(1-h)$

$=\cfrac{1}{2}\space\text{PT}(h+1-h)$

$=\cfrac{1}{2}\space\text{PT}$

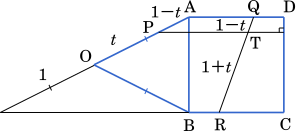
平行線と辺の比の性質より QT : TR = $(1-t):(1+t)$ が成り立つ。ベクトルの内分点の公式 $\cfrac{n\vec{a}+m\vec{b}}{m+n}$ を用いて

$\overrightarrow{\text{PT}}=\cfrac{1+t}{2}\bigg(\cfrac{2-t}{2}\vec{a}+\cfrac{t}{2}\vec{b}\bigg)+\cfrac{1-t}{2}\bigg(\cfrac{1-3t}{2}\vec{a}+\cfrac{3-t}{2}\vec{b}\bigg)$

$=\cfrac{(1+t)(2-t)+(1-t)(1-3t)}{4}\vec{a}+\cfrac{(1+t)t+(1-t)(3-t)}{4}\vec{b}$

$=\cfrac{2-t+2t-t^2+1-3t-t+3t^2}{4}\vec{a}+\cfrac{t+t^2+3-t-3t+t^2}{4}\vec{b}$

$=\bigg(\cfrac{1}{2}t^2-\cfrac{3}{4}t+\cfrac{3}{4}\bigg)(\vec{a}+\vec{b})$

ここで，$|\vec{a}+\vec{b}|=2$ より

$|\overrightarrow{\text{PT}}|=\bigg(\cfrac{1}{2}t^2-\cfrac{3}{4}t+\cfrac{3}{4}\bigg)|\vec{a}+\vec{b}|$

$=\bigg(\cfrac{1}{2}t^2-\cfrac{3}{4}t+\cfrac{3}{4}\bigg)\cdot2$

$=t^2-\cfrac{3}{2}t+\cfrac{3}{2}$

最小値を求めるためには，平方完成するとよい。

$=\bigg(t-\cfrac{3}{4}\bigg)^2-\cfrac{9}{16}+\cfrac{3}{2}$

$=\bigg(t-\cfrac{3}{4}\bigg)^2+\cfrac{15}{16}$

よって，PT は $t=\cfrac{3}{4}$ で最小になる。このとき $S$ を求めると

$S=\cfrac{1}{2}\cdot\cfrac{15}{16}=\cfrac{15}{32}$