【スマホで読む・わかりやすい】センター数学IIB2014追試【解説・正解・問題】

第２問

座標平面上で，放物線 $y=2x^2$ を $C$ とし，放物線 $y=-(x-p)^2+2$ を $D$ とする。 $C$ と $D$ は異なる 2 点で交わるとし，交点の $x$ 座標を $\alpha$，$\beta$（ただし，$\alpha < \beta$）とする。

(1)　整式 $2x^2$ と $-(x-p)^2+2$ の差を $f(x)$ とおくと

$f(x)=3x^2-\boxed{\text{ ア }}px+p^{\boxed{\text{イ}}}-2$

であり，$\alpha$ と $\beta$ は 2 次方程式 $f(x)=0$ の実数解である。$C$ と $D$ が異なる 2 点で交わることから，$p$ のとり得る値の範囲は

$-\sqrt{\boxed{\text{ ウ }}} < p < \sqrt{\boxed{\text{ ウ }}}$ である。このとき，$\alpha+\beta$ と $\beta-\alpha$ は $p$ を用いて

$\alpha+\beta=\cfrac{\boxed{\text{ エ }}}{\boxed{\text{ オ }}}p$，$\beta-\alpha=\cfrac{\boxed{\text{ カ }}\sqrt{\boxed{\text{ キ }}-2p^2}}{\boxed{\text{ オ }}}\cdots$①

と表される。

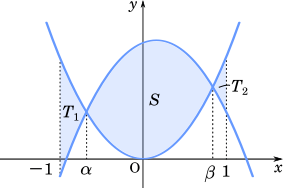
(2)　$-1 < p < 1$ のとき，二つの放物線 $C$，$D$ で囲まれた部分の面積を $S$ とする。また，直線 $x=-1$ と放物線 $C$，$D$ で囲まれた部分の面積を $T_1$ とし，直線 $x=1$ と放物線 $C$，$D$ で囲まれた部分の面積を $T_2$ とする。$-1 < \alpha < \beta < 1$ であるので，$\displaystyle T_1=\int_{-1}^{\alpha} f(x) dx$，$\displaystyle T_2=\int_{\beta}^{1} f(x)dx$ と表される。$p$ が $-1 < p < 1$ の範囲を動くとき，$S+T_1+T_2$ が最小になるときの $p$ の値を求めよう。

定積分 $\displaystyle\int_{-1}^{1} f(x)dx$ の値は $p$ を用いて

$\displaystyle\int_{-1}^{1} f(x)dx=\boxed{\text{ ク }}p^2-\boxed{\text{ ケ }}$

と表される。さらに，定積分の性質により

$\displaystyle\int_{-1}^{1} f(x)dx=\boxed{\text{ コ }}$

が成り立つ。$\boxed{\text{ コ }}$ に当てはまるものを，次の⓪～③のうちから一つ選べ。

⓪ $T_1+T_2-S$　① $T_1+T_2+S$

② $S-T_1-T_2$　③ $T_1+T_2+2S$

また，①により，$S$ は $p$ を用いて

$S=\cfrac{\boxed{\text{ サ }}}{\boxed{\text{ シス }}}(\boxed{\text{ セ }}-p^2)\sqrt{\boxed{\text{ ソ }}-2p^2}$

と表される。

そこで，$q=\sqrt{\boxed{\text{ ソ }}-2p^2}$ とおいて，$S+T_1+T_2$ を $q$ を用いて表すと

$S+T_1+T_2=\cfrac{\boxed{\text{ タ }}}{\boxed{\text{ チツ }}}q^3-q^2+\boxed{\text{ テ }}$

となる。

$-1 < p < 1$ のとき，$q$ のとり得る値の範囲は $\boxed{\text{ ト }} < q \leqq \sqrt{\boxed{\text{ ナ }}}$ である。$q$ がこの範囲を動くときの $S+T_1+T_2$ の値の増減を調べることにより，$S+T_1+T_2$ は $q=\cfrac{\boxed{\text{ ニ }}}{\boxed{\text{ ヌ }}}$ のとき，すなわち，$p=\pm\cfrac{\sqrt{\boxed{\text{ ネノ }}}}{\boxed{\text{ ハ }}}$ のとき，最小になることがわかる。

解答・解説

ア,イ 2,2　ウ 3　エ,オ 2,3

カ,キ 2,6　ク,ケ 2,2　コ 0

サ,シス,セ,ソ 8,27,3,6

タ,チツ,テ 8,27,4

ト,ナ 2,6　ニ,ヌ 9,4

ネノ,ハ 30,8

(1)

$f(x)=2x^2+(x-p)^2-2$

$=2x^2+x^2-2px+p^2-2$

$=3x^2-2px+p^2-2$

ここで $3x^2-2px+p^2-2=0$ とすると，判別式を用いて

$\cfrac{D}{4}=p^2-3(p^2-2)\gt0$

$-2p^2+6\gt0$

$p^2-3\lt0$

$(p+\sqrt{3})(p-\sqrt{3})\lt0$

$-\sqrt{3}\lt p\lt\sqrt{3}$

また解と係数の関係より

$\alpha+\beta=\cfrac{2}{3}p$

$\alpha\beta=\cfrac{p^2-2}{3}$

これを用いて

$(\alpha+\beta)^2=\cfrac{4}{9}p^2$

$\alpha^2+2\alpha\beta+\beta^2=\cfrac{4}{9}p^2$

$\alpha^2+\cfrac{2(p^2-2)}{3}+\beta^2=\cfrac{4}{9}p^2$

$\alpha^2+\beta^2=\cfrac{4p^2-6(p^2-2)}{9}$

$=\cfrac{12-2p^2}{9}$

また

$(\beta-\alpha)^2=\beta^2-2\alpha\beta+\alpha^2$

$=\cfrac{12-2p^2}{9}-\cfrac{2(p^2-2)}{3}$

$=\cfrac{12-2p^2-6(p^2-2)}{9}$

$=\cfrac{24-8p^2}{9}$

$\beta-\alpha=\sqrt{\cfrac{24-8p^2}{9}}$

$=\cfrac{2\sqrt{2(3-p^2)}}{3}$

$=\cfrac{2\sqrt{6-2p^2}}{3}$

したがって

$\alpha+\beta=\cfrac{2}{3}p$，$\beta-\alpha=\cfrac{2\sqrt{6-2p^2}}{3}\cdots\cdots$①

(2)

 

$\displaystyle\int_{\small{-1}}^{\small{1}}f(x)dx=[x^3-px^2+p^2x-2x]_{\small{-1}}^{\small{1}}$

$=(1-p+p^2-2)-(-1-p-p^2+2)$

$=2p^2-2$

$f(x)$ を $\alpha$ から $\beta$ の区間で積分すると負の値をとる。したがって

$\displaystyle\int_{\small{-1}}^{\small{1}}f(x)dx=T_1+T_2-S$

$S$ を求めると

$\displaystyle-S=\int_{\small{\alpha}}^{\small{\beta}}f(x)dx$

$=[x^3-px^2+p^2x-2x]_{\small{\alpha}}^{\small{\beta}}$

$=(\beta^3-\beta p^2+\beta p^2-2\beta)-(\alpha^3-\alpha^2 p+\alpha p^2-2\alpha)$

$=(\beta-\alpha)p^2-(\beta^2-\alpha^2)p+\beta^3-\alpha^3-2(\beta-\alpha)$

$=(\beta-\alpha)p^2-(\alpha+\beta)(\beta-\alpha)p+(\beta-\alpha)(\beta^2+\alpha\beta+\alpha^2)-2(\beta-\alpha)$

$=(\beta-\alpha)\{p^2-(\alpha+\beta)p+\alpha^2+\beta^2+\alpha\beta-2\}$

ここで①より

$=\cfrac{2\sqrt{6-2p^2}}{3}\bigg(p^2-\cfrac{2}{3}p^2+\cfrac{12-2p^2}{9}+\cfrac{p^2-2}{3}-2\bigg)$

$=\cfrac{2\sqrt{6-2p^2}}{3}\cdot\cfrac{9p^2-6p^2+12-2p^2+3p^2-6-18}{9}$

$=\cfrac{2\sqrt{6-2p^2}}{3}\cdot\cfrac{4p^2-12}{9}$

$=\cfrac{8}{27}(p^2-3)\sqrt{6-2p^2}$

$S=\cfrac{8}{27}(3-p^2)\sqrt{6-2p^2}$

次に $\displaystyle\int_{\small{-1}}^{\small{1}}f(x)dx=T_1+T_2-S=2p^2-2$ を利用して

$S+T_1+T_2=T_1+T_2-S+2S$

$=2p^2-2+\cfrac{16}{27}(3-p^2)\sqrt{6-2p^2}$

ここで $q=\sqrt{6-2p^2}$，$q^2=6-2p^2$ を利用することを考えて，式変形していくとよい。

$=2p^2-6+4+\cfrac{8}{27}(6-2p^2)\sqrt{6-2p^2}$

$=-(6-2p^2)+4+\cfrac{8}{27}(6-2p^2)\sqrt{6-2p^2}$

$=\cfrac{8}{27}q^3-q^2+4$

さらに，$-1\lt p\lt1$ を変形して $q$ の範囲を求めると

$-1\lt p\lt1$

$0\leqq p^2\lt1$

$-1\lt-p^2\leqq0$

$-2\lt-2p^2\leqq0$

$4\lt6-2p^2\leqq6$

$4\lt q^2\leqq 6$

$-1\lt p\lt1$ より $q$ はつねに正の数であるから

$2\lt q\leqq\sqrt{6}$

ここで，$g(q)=\cfrac{8}{27}q^3-q^2+4$ とすると

$g'(x)=\cfrac{8}{9}q^2-2q$

$\cfrac{8}{9}q^2-2q=0$ とおくと

$q\bigg(\cfrac{8}{9}q-2\bigg)=0$

$q=0,\cfrac{9}{4}$

$2\lt q\leqq\sqrt{6}$ より $q=\cfrac{9}{4}$

増減表を作ると

$\begin{aligned}q&&2&&\cdots&&\cfrac{9}{4}&&\cdots&&\sqrt{6}\\g'(q)&&&&-&&-&&+&&+\\g(q)&&&&\searrow&&\text{最小}&&\nearrow\end{aligned}$

$q=\cfrac{9}{4}$ のとき $p$ の値を求めると

$q^2=6-2p^2$

$\cfrac{81}{16}=6-2p^2$

$2p^2=\cfrac{96-81}{16}=\cfrac{15}{16}$

$p^2=\cfrac{15}{32}$

$p=\pm\sqrt{\cfrac{15}{32}}$

$=\pm\cfrac{\sqrt{15}}{4\sqrt{2}}$

$=\pm\cfrac{\sqrt{30}}{8}$