【スマホで読む・わかりやすい】センター数学IIB2014追試【解説・正解・問題】

第１問

〔1〕
不等式

$4\{\log_2 (3-\sqrt{x})\}^2+3\log_{\small\frac{1}{8}}(3-\sqrt{x})^2-2 > 0\cdots$①

を満たす $x$ のとり得る値の範囲を求めよう。

まず，真数は正であるから

$0 \leqq x \lt \boxed{\text{ ア }}\cdots$②

である。ただし，対数 $\log_a b$ に対し，$a$ を底といい，$b$ を真数という。

$y=\log_{\small\frac{1}{8}} (3-\sqrt{x})^2$ とおくと，$\bigg(\cfrac{1}{8}\bigg)^y=(3-\sqrt{x})^2$ である。 2 を底とする両辺の対数をとれば

$y=-\cfrac{\boxed{\text{ イ }}}{\boxed{\text{ ウ }}} \log_2 (3-\sqrt{x})$

であることがわかる。

よって，$X=\log_2(3-x)$ とおくと，①は

$\boxed{\text{ エ }}X^2-X-1 > 0\cdots$③

と表すことができる。

不等式③を解くと

$X < -\cfrac{1}{\boxed{\text{ オ }}}$，$X > \boxed{\text{ カ }}$

となり，$X=\log_2(3-\sqrt{x})$ により

$3-\sqrt{x} < \cfrac{\sqrt{\boxed{\text{ キ }}}}{\boxed{\text{ ク }}}$，$3-\sqrt{x} > \boxed{\text{ ケ }}\cdots$④

であることがわかる。②と④から，不等式①を満たす $x$ のとり得る値の範囲は

$0\leqq x < \boxed{\text{ コ }}$，$\cfrac{\boxed{\text{ サシ }}}{\boxed{\text{ ス }}}-\boxed{\text{ セ }}\sqrt{\boxed{\text{ キ }}} < x < \boxed{\text{ ア }}$

である。

〔2〕

$0\leqq\theta\leqq\cfrac{\pi}{2}$ として，$f(\theta)=8\sin\theta\cos\theta+6\cos^2 \theta$ とおく。

(1)　2 倍角の公式と三角関数の合成を用いると

$f(\theta)=\boxed{\text{ ソ }}\sin 2\theta+\boxed{\text{ タ }}(\cos 2\theta+1)$

$=\boxed{\text{ チ }}\sin( 2\theta+\alpha)+\boxed{\text{ タ }}\cdots$⑤

となる。ただし，$\alpha$ は

$\sin\alpha = \cfrac{\boxed{\text{ ツ }}}{\boxed{\text{ チ }}}$，$\cos\alpha=\cfrac{\boxed{\text{ テ }}}{\boxed{\text{ チ }}}$，$0 < \alpha < \cfrac{\pi}{2}$

を満たすものとする。

$0\leqq\theta\leqq\cfrac{\pi}{2}$ のとき，$2\theta+\alpha$ のとり得る値の範囲は

$\alpha\leqq 2\theta+\alpha\leqq\pi+\alpha$

であるから，$0 < \alpha < \cfrac{\pi}{2}$ に注意すると，$\sin(2\theta+\alpha)$ は，$\theta=\boxed{\text{ ト }}$ で最大値 $1$，$\theta=\boxed{\text{ ナ }}$ で最小値 $-\cfrac{\boxed{\text{ ニ }}}{\boxed{\text{ ヌ }}}$ をとることがわかる。ただし，$\boxed{\text{ ト }}$，$\boxed{\text{ ナ }}$ については，当てはまるものを，次の⓪～⑤のうちから一つずつ選べ。

⓪ $0$　① $\cfrac{\pi}{4}-\alpha$

② $\cfrac{\pi}{4}-\cfrac{\alpha}{2}$　③ $\cfrac{\pi}{2}-\alpha$

④ $\cfrac{\pi}{2}-\cfrac{\alpha}{2}$　⑤ $\cfrac{\pi}{2}$

以上のことから，$0\leqq\theta\leqq\cfrac{\pi}{2}$ のとき，$f(\theta)$ のとり得る値の範囲は $\boxed{\text{ ネ }}\leqq f(\theta)\leqq \boxed{\text{ ノ }}$ である。

(2)　$f(\theta)=6$，$0\leqq\theta\leqq\cfrac{\pi}{2}$ を満たす $\theta$ を求めよう。⑤を用いると，$f(\theta)=6$ から

$\sin(2\theta+\alpha)=\cfrac{\boxed{\text{ ハ }}}{\boxed{\text{ ヒ }}}$

である。ここで，$\sin\alpha=\cfrac{\boxed{\text{ ツ }}}{\boxed{\text{ テ }}}$ と，すべての $x$ について $\sin(\pi-x)=\boxed{\text{ フ }}$ であることに注意すると，求める $\theta$ は $\boxed{\text{ ヘ }}$ と $\boxed{\text{ ホ }}$ であることがわかる。ただし，$\boxed{\text{ フ }}$ については，当てはまるものを，次の⓪～③ のうちから一つ選べ。

⓪ $\cos x$　① $-\cos x$　② $\sin x$　③ $-\sin x$

また，$\boxed{\text{ ヘ }}$，$\boxed{\text{ ホ }}$ については，当てはまるものを，次の⓪～⑤のうちから一つずつ選べ。$\boxed{\text{ ヘ }}$ と $\boxed{\text{ ホ }}$ は解答の順序を問わない。

⓪ $0$　① $\alpha$　② $\cfrac{\pi}{2}-\alpha$

③ $\cfrac{\pi}{2}$　④ $\pi-2\alpha$　⑤ $\pi-\alpha$

[ad]

解答・解説

ア 9　イ,ウ 2,3　エ 2

オ,カ 2,1　キ,ク 2,2

ケ 2　コ 1

サシ,ス,セ 19,2,3

ソ 4　タ 3　チ 5

ツ,テ 3,4　ト 2

ナ 5　ニ,ヌ 3,5

ネ,ノ 0,8　ハ,ヒ 3,5

フ 2

ヘ,ホ 0,2 または 2,0

〔1〕

(1)

真数条件（真数は 0 以上の数）から

$3-\sqrt{x}\gt0$

$\sqrt{x}\lt3$

$x\lt9$

したがって $0\leqq\lt x\lt9\cdots\cdots$②

次に $\bigg(\cfrac{1}{8}\bigg)^y=(3-\sqrt{x})^2$ の両辺の 2 を底とする対数をとると

$\log_2\bigg(\cfrac{1}{8}\bigg)^y=\log_2 (3-\sqrt{x})^2$

$y\log_2\cfrac{1}{8}=2\log_2(3-\sqrt{x})$

$y(\log_2 1-\log_2 8=2\log_2(3-\sqrt{x})$

$y(0-3)=2\log_2(3-\sqrt{x})$

$y=-\cfrac{2}{3}\log_2(3-\sqrt{x})$

$X=\log_2(3-\sqrt{x})$ とおくと，①は

$4X^2+3y-2\gt0$

$4x^2+3\bigg(-\cfrac{2}{3}\bigg)X-2\gt0$

$4X^2-2X-2\gt0$

$2X^2-X-1\gt0\cdots\cdots$③

これを解くと

$(2X+1)(X-1)\gt0$

$X\lt-\cfrac{1}{2},X\gt1$

$X=\log_2(3-\sqrt{x})$ より

$\log_2(3-\sqrt{x})\lt-\cfrac{1}{2}$

ここで $\log_a c=b$ は $a^b=c$ と表すことができることを考えると

$3-\sqrt{x}\lt2^{-\small\frac{1}{2}}$

$3-\sqrt{x}\lt\cfrac{1}{2^{\small\frac{1}{2}}}$

$3-\sqrt{x}\lt\cfrac{1}{\sqrt{2}}$

$3-\sqrt{x}\lt\cfrac{\sqrt{2}}{2}$

また

$\log_2(3-\sqrt{x})\gt1$

$3-\sqrt{x}\gt2$

したがって

$3-\sqrt{x}\lt\cfrac{\sqrt{2}}{2},3-\sqrt{x}\gt2\cdots\cdots$④

$x$ のとり得る範囲を求めると④より

$3-\sqrt{x}\lt\cfrac{\sqrt{2}}{2}$

$\sqrt{3}\gt3-\cfrac{\sqrt{2}}{2}$

$x\gt\bigg(3-\cfrac{\sqrt{2}}{2}\bigg)^2$

$x\gt9-3\sqrt{2}+\cfrac{1}{2}$

$x\gt\cfrac{19}{2}-3\sqrt{2}$

ここで $\cfrac{19}{2}-3\sqrt{2}$ を考えると

$1\lt\sqrt{2}\lt2$

$3\lt3\sqrt{2}\lt6$

$-6\lt-3\sqrt{2}\lt-3$

$\cfrac{19}{2}-6\lt\cfrac{19}{2}-3\sqrt{2}\lt\cfrac{19}{2}-3$

$\cfrac{7}{2}\lt\cfrac{19}{2}-3\sqrt{2}\lt\cfrac{13}{2}$

また

$3-\sqrt{x}\gt2$

$\sqrt{x}\lt1$

両辺を 2 乗して

$x\lt1$

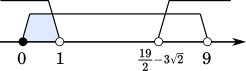
したがって

$0\leqq x\lt1,\cfrac{19}{2}-3\sqrt{2}\lt x\lt9$