【スマホで読む・わかりやすい】センター数学IIB2014本試【解説・正解・問題】

第４問

座標空間において，立方体 OABC ‐DEFG の頂点を

O(0,0,0)，A(3,0,0)，B(3,3,0)，C(0,3,0)，

D(0,0,3)，E(3,0,3)，F(3,3,3)，G(0,3,3)

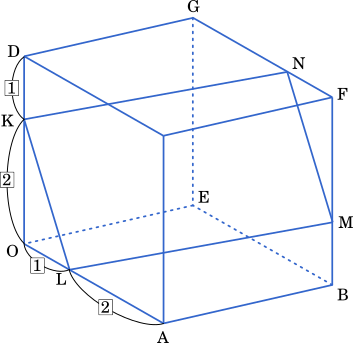
とし， OD を $2:1$ に内分する点を K，OA を $1:2$ に内分する点を L とする。 BF 上の点 M，FG 上の点 N および K，L の 4 点は同一平面上にあり，四角形 KLMN は平行四辺形であるとする。

(1)　四角形 KLMN の面積を求めよう。ベクトル $\overrightarrow{\text{LK}}$ を成分で表すと

$\overrightarrow{\text{LK}}=(\boxed{\text{ アイ }},\boxed{\text{ ウ }},\boxed{\text{ エ }})$

となり，四角形 KLMN が平行四辺形であることにより，$\overrightarrow{\text{LK}}=\boxed{\text{ オ }}$ である。$\boxed{\text{ オ }}$ に当てはまるものを，次の⓪～③のうちから一つ選べ。

⓪ $\overrightarrow{\text{ML}}$　① $\overrightarrow{\text{LM}}$

② $\overrightarrow{\text{NM}}$　③ $\overrightarrow{\text{MN}}$

ここで，M$(3,3,s)$，N$(t,3,3)$ と表すと，$\overrightarrow{\text{LK}}=\boxed{\text{ オ }}$ であるので，$s=\boxed{\text{ カ }}$，$t=\boxed{\text{ キ }}$ となり， N は FG を $1:\boxed{\text{ ク }}$ に内分することがわかる。
また，$\overrightarrow{\text{LK}}$ と $\overrightarrow{\text{LM}}$ について

$\overrightarrow{\text{LK}}\cdot\overrightarrow{\text{LM}}=\boxed{\text{ ケ }}$，$|\overrightarrow{\text{KL}}| =\sqrt{\boxed{\text{ コ }}}$，$|\overrightarrow{\text{LM}}| =\sqrt{\boxed{\text{ サシ }}}$

となるので，四角形 KLMN の面積は $\sqrt{\boxed{\text{ スセ }}}$ である。

(2)　四角形 KLMN を含む平面を $\alpha$ とし，点 O を通り平面 $\alpha$ と垂直に交わる直線を $\ell$，$\alpha$ と $\ell$ の交点を P とする。 $|\overrightarrow{\text{OP}}|$ と三角錐 OLMN の体積を求めよう。

P$(p,q,r)$ とおくと，$\overrightarrow{\text{OP}}$ は $\overrightarrow{\text{LK}}$ および $\overrightarrow{\text{LM}}$ と垂直であるから，

$\overrightarrow{\text{OP}}\cdot\overrightarrow{\text{LK}}=\overrightarrow{\text{OP}}\cdot\overrightarrow{\text{LM}}=\boxed{\text{ ソ }}$ となるので，$p=\boxed{\text{ タ }}\space r$，$p=\cfrac{\boxed{\text{ チツ }}}{\boxed{\text{ テ }}}\space r$ であることがわかる。$\overrightarrow{\text{OP}}$ と $\overrightarrow{\text{PL}}$ が垂直であることにより $r=\cfrac{\boxed{\text{ ト }}}{\boxed{\text{ ナニ }}}$ となり，$|\overrightarrow{\text{OP}}|$ を求めると

$|\overrightarrow{\text{OP}}|=\cfrac{\boxed{\text{ ヌ }}\sqrt{\boxed{\text{ ネノ }}}}{\boxed{\text{ ハヒ }}}$

である。$|\overrightarrow{\text{OP}}|$ は三角形 LMN を底面とする三角錐 OLMN の高さであるから，三角錐 OLMN の体積は $\boxed{\text{ フ }}$ である。

解答・解説

アイ,ウ,エ $-1,0,2$　オ $3$

カ,キ $1,2$　ク $2$　ケ $0$

コ $5$　サシ $14$　スセ $70$

ソ $0$　タ,チツ,テ $2,-5,3$

ト,ナニ $9,35$

ヌ,ネノ,ハヒ $3,70,35$

フ $1$

(1)

$\overrightarrow{\text{LK}}=\overrightarrow{\text{OK}}-\overrightarrow{\text{OL}}$

ここで

$\overrightarrow{\text{OK}}=\cfrac{2}{3}\overrightarrow{\text{OD}}=\cfrac{2}{3}(0,0,3)=(0,0,2)$

$\overrightarrow{\text{OL}}=\cfrac{1}{3}\overrightarrow{\text{OA}}=\cfrac{1}{3}(3,0,0)=(1,0,0)$

だから

$\overrightarrow{\text{LK}}=(0,0,2)-(1,0,0)$

$=(-1,0,2)$

また，四角形KLMN が平行四辺形であることにより，$\overrightarrow{\text{LK}}=\overrightarrow{\text{MN}}$ である。

$\overrightarrow{\text{MN}}=\overrightarrow{\text{ON}}-\overrightarrow{\text{OM}}$

$=(t,3,3)-(3,3,s)$

$=(t-3,0,3-s)$

これを $\overrightarrow{\text{LK}}$ と比べると

$t-3=-1$ より $t=2$

$3-s=2$ より $s=1$

よって $\overrightarrow{\text{OM}}=(3,3,1)$，$\overrightarrow{\text{ON}}=(2,3,3)$ となる。

したがって，N は FG を 1 : 2 に内分する。

次に

$\overrightarrow{\text{LM}}=\overrightarrow{\text{OM}}-\overrightarrow{\text{OL}}$

$=(3,3,1)-(1,0,0)$

$=(2,3,1)$

より

$\overrightarrow{\text{LK}}\cdot\overrightarrow{\text{LM}}=(-1)\cdot2+0\cdot3+2\cdot1=0$

内積が 0 であることから，∠KLM は直角であることが分かる。つまり四角形 KLMN は長方形である。

$|\overrightarrow{\text{LK}}|=\sqrt{(-1)^2+0^2+2^2}$

$=\sqrt{5}$

$|\overrightarrow{\text{LM}}|=\sqrt{2^2+3^2+1^2}$

$=\sqrt{14}$

となり，四角形 KLMN の面積は

$S=\sqrt{5}\times\sqrt{14}=\sqrt{70}$

(2)

図

$\overrightarrow{\text{OP}}$ は $\overrightarrow{\text{LK}}$ および $\overrightarrow{\text{LM}}$ と垂直であるから

$\overrightarrow{\text{OP}}\cdot\overrightarrow{\text{LK}}=\overrightarrow{\text{OP}}\cdot\overrightarrow{\text{LM}}=0$

となる。

$\overrightarrow{\text{OP}}\cdot\overrightarrow{\text{LK}}=p(-1)+q\cdot 0+r\cdot2=-p+2r=0$

$\overrightarrow{\text{OP}}\cdot\overrightarrow{\text{LM}}=p\cdot2+q\cdot3+1\cdot r=2p+3q+r=0$

上の式より $p=2r$ となり，これを下の式に代入して

$4r+3q+r=0$

$q=-\cfrac{5}{3}r$

また問題文より $\overrightarrow{\text{OP}}\cdot\overrightarrow{\text{PL}}=0$ だから

$\overrightarrow{\text{PL}}=\overrightarrow{\text{OL}}-\overrightarrow{\text{OP}}$

$=(1,0,0)-(p,q,r)$

$=(1-p,-q,-r)$

より

$\overrightarrow{\text{OP}}\cdot\overrightarrow{\text{PL}}=p(1-p)-q^2-r^2=0$

これに $p=2r$，$q=-\cfrac{5}{3}r$ を代入して

$2r(1-2r)-\cfrac{25}{9}r^2-r^2=0$

$2r-4r^2-\cfrac{25}{9}r^2-r^2=0$

$2r-\cfrac{70}{9}r^2=0$

$\cfrac{35}{9}r^2-r=0$

$35r^2-9r=0$

$35r(r-\cfrac{35}{9})=0$

$r=0,\cfrac{9}{35}$

$p$ は原点ではないので $r=\cfrac{9}{35}$

よって

$p=2\cdot\cfrac{9}{35}=\cfrac{18}{35}$

$r=-\cfrac{5}{3}\cdot\cfrac{9}{35}=-\cfrac{3}{7}$

したがって P$\bigg(\cfrac{18}{35},-\cfrac{3}{7},\cfrac{9}{35}\bigg)$

$|\overrightarrow{\text{OP}}|$ を求めると

$|\overrightarrow{\text{OP}}|=\sqrt{\bigg(\cfrac{18}{35}\bigg)^2+\bigg(-\cfrac{3}{7}\bigg)^2+\bigg(\cfrac{9}{35}\bigg)^2}$

$=\sqrt{\cfrac{3^2}{35^2}\{6^2+(-5)^2+3^2\}}$

$=\sqrt{\cfrac{3^2\cdot70}{35^2}}$

$=\cfrac{3\sqrt{70}}{35}$