【スマホで読む・わかりやすい】センター数学IIB2014本試【解説・正解・問題】

第２問

$p$ を実数とし，$f(x)=x^3-px$ とする。

(1)　関数 $f(x)$ が極値をもつための $p$ の条件を求めよう。$f(x)$ の導関数は，$f′(x)=\boxed{\text{ ア }}x^{\boxed{\text{イ}}}-p$ である。したがって，$f(x)$ が $x=a$ で極値をとるならば，$f′(x)=\boxed{\text{ ア }}x^{\boxed{\text{イ}}}-p=\boxed{\text{ ウ }}$ が成り立つ。さらに，$x=a$ の前後での $f′(x)$ の符号の変化を考えることにより，$p$ が条件 $\boxed{\text{ エ }}$ を満たす場合は，$f(x)$ は必ず極値をもつことがわかる。$\boxed{\text{ エ }}$ に当てはまるものを，次の⓪〜④のうちから一つ選べ。

⓪ $p=0$　① $p > 0$　② $p \geqq 0$　③ $p < 0$ 　④ $p\leqq 0$

(2)　関数 $f(x)$ が $x=\cfrac{p}{3}$ で極値をとるとする。また，曲線 $y=f(x)$ を $C$ とし，$C$ 上の点 $\bigg(\cfrac{p}{3},f\bigg(\cfrac{p}{3}\bigg)\bigg)$ を A とする。

$f(x)$ が $x=\cfrac{p}{3}$ で極値をとることから，$p=\boxed{\text{ オ }}$ であり，$f(x)$ は $x=\boxed{\text{ カキ }}$ で極大値をとり，$x=\boxed{\text{ ク }}$ で極小値をとる。

曲線 $C$ の接線で，点 A を通り傾きが $0$ でないものを $\ell$ とする。 $\ell$ の方程式を求めよう。$\ell$ と $C$ の接点の $x$ 座標を $b$ とすると，$\ell$ は点 $(b,f(b))$ における $C$ の接線であるから，$\ell$ の方程式は $b$ を用いて

$y=(\boxed{\text{ ケ }}b^2-\boxed{\text{ コ }})(x-b)+f(b)$

と表すことができる。また，$\ell$ は点 A を通るから，方程式

$\boxed{\text{ サ }}b^3-\boxed{\text{ シ }}b^2+1=0$

を得る。この方程式を解くと，$b=\boxed{\text{ ス }}$，$\cfrac{\boxed{\text{ セソ }}}{\boxed{\text{ タ }}}$ であるが，$\ell$ の傾きが $0$ でないことから，$\ell$ の方程式は

$y=\cfrac{\boxed{\text{ チツ }}}{\boxed{\text{ テ }}}x+\cfrac{\boxed{\text{ ト }}}{\boxed{\text{ ナ }}}$

である。

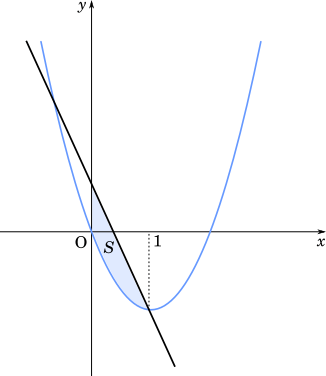
点 A を頂点とし，原点を通る放物線を $D$ とする。$\ell$ と $D$ で囲まれた図形のうち，不等式 $x\geqq 0$ の表す領域に含まれる部分の面積 $S$ を求めよう。 $D$ の方程式は

$y=\boxed{\text{ ニ }}x^2-\boxed{\text{ ヌ }}x$

であるから，定積分を計算することにより，$S=\cfrac{\boxed{\text{ ネノ }}}{24}$ となる。

解答・解説

ア,イ $3,2$　ウ $0$　エ $1$

オ $3$　カキ,ク $-1,1$

ケ,コ $3,3$　サ,シ $2,3$

ス,セソ,タ $1,-1,2$

チツ,テ,ト,ナ $-9,4,1,4$

ニ,ヌ $2,4$　ネノ $11$

(1)

$f(x)=x^2-px$ を $x$ で微分すると

$f'(x)=3x^2-p$

$f(x)$ が $x=a$ で極値をとるとき，$3a^2-p=0$ が成り立つ。また，$f(x)$ が極値を持つとき，$f'(a)$ の前後で符号が入れ替わる。ここから，$f'(a)$ が正の数と負の数の両方をとる場合を考えるとよい。

$f'(a)=3a^2-p$ であり，$3a^2$ は $a=0$ で $0$ となり，それ以外では常に正の値をとる。つまり，$f'(a)$ が正の数と負の数の両方の値をとるためには，$p>0$ であればよい。

(2)

$f(x)$ が $x=\cfrac{p}{3}$ で極値をとるので

$f’\bigg(\cfrac{p}{3}\bigg)=3\bigg(\cfrac{p}{3}\bigg)^2-p=0$

$\cfrac{p^2}{3}-p=0$

$p^2-3=0$

$p(p-3)=0$

$p=0,3$

$p\gt0$ より $p=3$

これを用いて，$f(x)$ の極値を求めると

$f'(x)=3x^2-3$

$f(x)$ が極値をとるとき

$3x^2-3=0$

$3(x^2-1)=0$

$3(x+1)(x-1)=0$

$x=-1,1$

$\begin{aligned}x&&\cdots&&-1&&\cdots&&1&&\cdots\\f'(x)&&+&&0&&-&&0&&+\\f(x)&&\nearrow&&2&&\searrow&&-2&&\nearrow\end{aligned}$

$f(-1)=(-1)^3-3\cdot(-1)=2$

$f(1)=1^3-3\cdot1=-2$

したがって，$f(x)$ は $x=-1$ で極大値をとり，$x=1$ で極小値をとる。

次に，$\ell$ の方程式を求めると，$f'(x)=3x-3$ だから

$f'(b)=3b^2-3$

これが，$\ell$ の傾きを表すので，直線の式は

$y=(3b^2-3)(x-b)+f(b)$

となる。これに A$(1,-2)$ と $f(b)$ の値を代入して

$-2=(3b^2-3)(1-b)+b^3-3b$

$3b^2-3b^3-3+36+b^3-3b+2=0$

$2b^3-3b^2+1=0$

解を求めると，式は $b=1$ のとき $0$ となるので $(b-1)$ で割り切れる。組み立て除法を用いて

$\begin{aligned}2&&-3&&0&&1&&|\underline{1}\\&&2&&-1&&-1\\\hline 2&&-1&&-1&&0\end{aligned}$

$(b-1)(2b^2-b-1)=0$

$(b-1)(2b+1)(b-1)=0$

$(b-1)^2(2b+1)=0$

$b=1,-\cfrac{1}{2}$

$b=1$ のとき，接線の傾きは $0$ となるので $b=-\cfrac{1}{2}$

これを $\ell$ の方程式に代入すると

$y=\bigg\{3\bigg(-\cfrac{1}{2}\bigg)^2-3\bigg\}\bigg(x+\cfrac{1}{2}\bigg)+f\bigg(-\cfrac{1}{2}\bigg)$

$=\bigg(\cfrac{3}{4}-3\bigg)\bigg(x+\cfrac{1}{2}\bigg)+\bigg(-\cfrac{1}{2}\bigg)^3-3\bigg(-\cfrac{1}{2}\bigg)$

$=-\cfrac{9}{4}\bigg(x+\cfrac{1}{2}\bigg)-\cfrac{1}{8}+\cfrac{3}{2}$

$=-\cfrac{9}{4}x-\cfrac{9}{8}+\cfrac{11}{8}$

$=-\cfrac{9}{4}x+\cfrac{1}{4}$

さらに，$D$ の方程式を求めると $D$ は点 A$(1,-2)$ を通るので

$y=c(x-1)^2-2$

とおくことができる。これが原点を通るので

$0=c(-1)^2-2$

$c=2$

となる。よって $D$ は

$y=2(x-1)^2-2$

$=2x^2-4x+2-2$

$=2x^2-4x$

面積 $S$ を求めると

$\displaystyle S=\int_0^1 -\cfrac{9}{4}x+\cfrac{1}{4}-2x^2+4x\space dx$

$\displaystyle =\int_0^1 -2x^2+\cfrac{7}{4}x+\cfrac{1}{4}\space dx$

$=\bigg[-\cfrac{2}{3}x^3+\cfrac{7}{8}x^2+\cfrac{1}{4}x\bigg]_0^1$

$=-\cfrac{2}{3}+\cfrac{7}{8}+\cfrac{1}{4}$

$=\cfrac{-16+21+6}{24}$

$=\cfrac{11}{24}$