【スマホで読む・わかりやすい】センター数学IIB2014本試【解説・正解・問題】

第１問

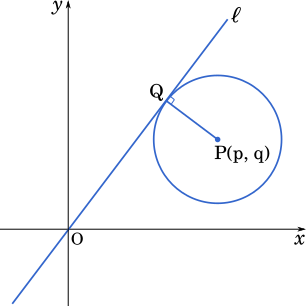
〔1〕　O を原点とする座標平面において，点 P$(p,q)$ を中心とする円 $C$ が，方程式 $y=\cfrac{4}{3}x$ で表される直線 $\ell$ に接しているとする。

(1)　円 $C$ の半径 $r$ を求めよう。

点 P を通り直線 $\ell$ に垂直な直線の方程式は

$y=-\cfrac{\boxed{\text{ ア }}}{\boxed{\text{ イ }}}(x-p)+q$
なので， P から $\ell$ に引いた垂線と $ell$ の交点 Q の座標は

$\bigg(\cfrac{3}{25}\bigg(\boxed{\text{ ウ }}p+\boxed{\text{ エ }}q\bigg)$,$\cfrac{4}{25}\bigg(\boxed{\text{ ウ }}p+\boxed{\text{ エ }}q\bigg)\bigg)$

となる。
求める C の半径 $r$ は，P と $\ell$ の距離 PQ に等しいので

$r=\cfrac{1}{5}|\boxed{\text{ オ }}p-\boxed{\text{ カ }}q|\cdots$①

である。

(2)　円 C が，$x$ 軸に接し，点 R$(2,2)$ を通る場合を考える。このとき， $p > 0$，$q > 0$ である。$C$ の方程式を求めよう。

$C$ は $x$ 軸に接するので，$C$ の半径 $r$ は $q$ に等しい。したがって，①により，$p=\boxed{\text{ キ }}q$ である。

$C$ は点 R を通るので，求める $C$ の方程式は

$(x-\boxed{\text{ ク }})^2+(y-\boxed{\text{ ケ }})^2=\boxed{\text{ コ }}\cdots$②

または

$(x-\boxed{\text{ サ }})^2+(y-\boxed{\text{ シ }})^2=\boxed{\text{ ス }}\cdots$③

であることがわかる。ただし，$\boxed{\text{ コ }} < \boxed{\text{ ス }}$ とする。

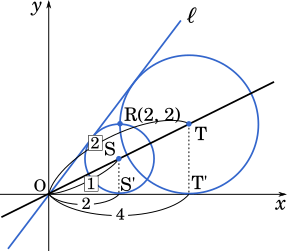
(3)　方程式②の表す円の中心を S， 方程式③の表す円の中心を T とおくと，直線 ST は原点 O を通り，点 O は線分 ST を $\boxed{\text{ セ }}$ する。$\boxed{\text{ セ }}$ に当てはまるものを，次の⓪～⑤のうちから一つ選べ。

⓪ $1:1$ に内分　① $1:2$ に内分

② $2:1$ に内分　③ $1:1$ に外分

④ $1:2$ に外分　⑤ $2:1$ に外分

〔2〕　自然数 $m$，$n$ に対して，不等式

$\log_2 {m^3}+\log_3 n^2 \leqq 3\cdots$④

を考える。

$m=2$，$n=1$ のとき，$\log_2 m^3+log_3 n^2=\boxed{\text{ ソ }}$ であり，この $m$，$n$ の値の組は④を満たす。

$m=4$，$n=3$ のとき，$\log_2 m^3+\log_3 n^2=\boxed{\text{ タ }}$ であり，この $m$，$n$ の値の組は④を満たさない。

不等式④を満たす自然数 $m$，$n$ の組の個数を調べよう。④は

$\log_2 m+\cfrac{\boxed{\text{ チ }}}{\boxed{\text{ ツ }}}\log_3 n \leqq \boxed{\text{ テ }}\cdots$⑤

と変形できる。

$n$ が自然数のとき，$\log_3 n$ のとり得る最小の値は $\boxed{\text{ ト }}$ であるから，⑤により，$\log_2 m \leqq \boxed{\text{ テ }}$ でなければならない。$\log_2 m\leqq \boxed{\text{ テ }}$ により，$m=\boxed{\text{ ナ }}$ または $m=\boxed{\text{ ニ }}$ でなければならない。ただし，$\boxed{\text{ ナ }} < \boxed{\text{ ニ }}$ とする。

$m= \boxed{\text{ ナ }}$ の場合，⑤は，$\log_3 n\leqq \cfrac{\boxed{\text{ ヌ }}}{\boxed{\text{ ネ }}}$ となり，$n^2 \leqq \boxed{\text{ ノハ }}$ と変形できる。よって，$m=\boxed{\text{ ナ }}$ のとき，⑤を満たす自然数 $n$ のとり得る値の範囲は $n \leqq \boxed{\text{ ヒ }}$ である。したがって，$m=\boxed{\text{ ナ }}$ の場合，④を満たす自然数 $m$，$n$ の組の個数は $\boxed{\text{ ヒ }}$ である。

同様にして，$m=\boxed{\text{ ニ }}$ の場合，④を満たす自然数 $m$，$n$ の組の個数は $\boxed{\text{ フ }}$ である。

以上のことから，④を満たす自然数 $m$，$n$ の組の個数は $\boxed{\text{ ヘ }}$ である。

解答・解説

ア,イ $3,4$　ウ,エ $3,4$

オ,カ $4,3$　キ $2$

ク,ケ,コ $2,1,1$　サ,シ,ス $4,2,4$

セ $4$　ソ $3$　タ $8$

チ,ツ $2,3$　テ $1$　ト $0$

ナ $1$　ニ $2$　ヌ,ネ $3,2$

ノハ $27$　ヒ $5$

フ $1$　ヘ $6$

〔1〕

(1)

直線 $\ell$ に垂直な直線の傾きを $m$ とおくと，$\cfrac{4}{3}m=-1$ が成り立つことから，$m=-\cfrac{3}{4}$ である。よって

$y=-\cfrac{3}{4}(x-p)+q$

点 Q の座標を求めるために，これを $\ell$ と連立すると

$\cfrac{4}{3}x=-\cfrac{3}{4}(x-p)+q$

$16x=-9(x-p)+12q$

$16x=-9x+9p+12q$

$25x=9p+12q$

$x=\cfrac{3}{25}(3p+4q)$

これを $\ell$ に代入して

$y=\cfrac{4}{3}\cdot\cfrac{3}{25}(3p+4q)$

$=\cfrac{4}{25}(3p+4q)$

したがって，点 Q の座標は

$\bigg(\cfrac{3}{25}(3p+4q),\space\cfrac{4}{25}(3p+4q)\bigg)$

次に距離 PQ を求める。点 Q の座標が分かっているので三平方の定理を用いて求めることになるが，ここは点と直線の距離の公式を用いて求めた方がよいだろう。

$r=\cfrac{\bigg|\cfrac{4}{3}p-q\bigg|}{\sqrt{\bigg(\cfrac{4}{3}\bigg)^2+(-1)^2}}$

$=\cfrac{\bigg|\cfrac{4}{3}p-q\bigg|}{\sqrt{\cfrac{25}{9}}}$

$=\cfrac{\bigg|\cfrac{4}{3}p-q\bigg|}{\cfrac{5}{3}}$

$=\cfrac{\bigg|\cfrac{4}{3}p-q\bigg|\times\cfrac{3}{5}}{\cfrac{5}{3}\times\cfrac{3}{5}}$

$=\cfrac{3}{5}\space\bigg|\cfrac{4}{3}p-q\bigg|$

$=\cfrac{1}{5}\space|4p-3q|$

(2)

$r=q$ だから

$q=\cfrac{1}{5}|4p-3q|$

絶対を外すと

$4p-3q\geqq0$ のとき

$q=\cfrac{1}{5}(4p-3q)$

$5q=4p-3q$

$p=2q$

また $4p-3q < 0$ のとき

$q=\cfrac{1}{5}(-4p+3q)$

$5q=-4p+3q$

$p=-\cfrac{1}{2}q$

これは $p\gt0$，$q\gt0$ より成り立たない。

したがって $p=2q$

次に円 $C$ の方程式を求める。式を $(x-p)^2+(y-q)^2=r^2$ とおいて，これが点 R $(2,2)$ を通ることと，$p=2q$，$r=q$ であることから

$(2-2q)^2+(2-q)^2=q^2$

$4-8q+4q^2+4-4q+q^2=q^2$

$4q^2-12q+8=0$

$q^2-3q+2=0$

$(q-1)(q-2)=0$

$q=1,2$

よって，$(p,q)=(2,1),(4,2)$

$(p,q)=(2,1)$ のとき

$C:(x-2)^2+(y-1)^2=1$

$(p,q)=(4,2)$ のとき

$C:(x-4)^2+(y-2)^2=4$

(3)

図より，$S:T=S’:T’=1:2$

したがって，点 O は線分 ST を 1:2 に外分する。

〔2〕

$\log_2 m^3+\log_3 n^2\leqq 3\cdots$④

を変形すると

$=3\log_2 m+2\log_3 n$

$m=2$，$n=1$ のとき

$3\log_2 2+2\log_3 1$

$=3\cdot1+2\cdot0=3$

$m=4$，$n=3$ のとき

$3\log_2 4+2\log_3 3$

$=3\cdot2+2\cdot1=8$

$=3\log_2 m+2\log_3 n$ の両辺を 3 で割って

$\log_2 m+\cfrac{2}{3}\log_3 n\leqq 1\cdots$⑤

ここで，$\log_3 n$ は $n=1$ で最小値 $0$ となる。よって $\log_2 m\leqq 1$ となるので，当てはまる $m$ は $m=1,2$ である。

$m=1$ のとき⑤は

$\log_2 1+\cfrac{2}{3}\log_2 n\leqq1$

$\cfrac{2}{3}\log_2 n\leqq1$

$2\log_2 n\leqq 3$

$\log_3 n^2\leqq 3$

ここで，$3^3=27$ であることから

$n^2\leqq 27$

が成り立つ。これに当てはまる自然数 $n$ で最大のものは $n=5$ だから

$n\leqq5$

また $m=2$ のとき⑤は

$\log_2 2+\cfrac{2}{3}\log_3 n\leqq1$

$1+\cfrac{2}{3}\log_3 n\leqq 1$

$\cfrac{2}{3}\log_3 n\leqq 0$

$\log_3 n\leqq 0$

これを満たす自然数 $n$ は $n=1$ のみである。

したがって，④を満たす自然数 $m,n$ の組の個数は $5+1=6$ である。