【スマホで読む・わかりやすい】センター数学IIB2013追試【解説・正解・問題】

第２問

座標平面上で，放物線 $y=x^2$ を $C$ とし，2点 P$(a,a^2)$，Q$(b,b^2)$ における $C$ の接線をそれぞれ $\ell$，$m$ とする。ただし，$a > 0$ であり，$\ell$ と $m$ は垂直であるとする。

$\ell$ と $m$ は垂直であるから，関係式 $\boxed{\text{ ア }}ab=-1$ が成り立つ。したがって，$\ell$ と $m$ の交点 R の座標は，$a$ を用いて

$\bigg(\cfrac{1}{\boxed{\text{ イ }}}\bigg(a-\cfrac{\boxed{\text{ ウ }}}{\boxed{\text{ エ }}a}\bigg),-\cfrac{\boxed{\text{ オ }}}{\boxed{\text{ カ }}}\bigg)$

と表される。

点 P を通り $\ell$ に垂直な直線を $\ell’$ とし，点 Q を通り $m$ に垂直な直線を $m’$ とする。$\ell’$ と $m’$ の交点 T の座標は，$a$ を用いて

$\bigg(\cfrac{1}{\boxed{\text{ キ }}}\bigg(a-\cfrac{\boxed{\text{ ク }}}{\boxed{\text{ ケ }}a}\bigg),\space a^2+\cfrac{1}{\boxed{\text{ コサ }}a^2}+\cfrac{1}{\boxed{\text{ シ }}}\bigg)$

と表される。

$a$ の値が変化するとき，点 T の軌跡は放物線

$y=\boxed{\text{ ス }}x^2+\cfrac{\boxed{\text{ セ }}}{\boxed{\text{ ソ }}}$

である。

四角形 PTQR の面積を $S_1$ とすると

$S_1=\cfrac{1}{\boxed{\text{ タ }}}\bigg(a+\cfrac{1}{\boxed{\text{ チ }}a}\bigg)^{\boxed{\text{ツ}}}$

が成り立つ。
一方，放物線 $C$ と直線 PQ で囲まれた図形の面積は

$\cfrac{1}{\boxed{\text{ テ }}}\bigg(a+\cfrac{1}{\boxed{\text{ ト }}a}^{\boxed{\text{ナ}}}\bigg)$

である。

したがって，放物線 $C$ と接線 $\ell$，$m$ で囲まれた図形の面積を $S_2$ とすると

$S_2=\cfrac{\boxed{\text{ ニ }}}{\boxed{\text{ ヌ }}}S_1$

が成り立つ。また，相加平均と相乗平均の関係を利用して，$S_2$ は $a=\cfrac{1}{\boxed{\text{ ネ }}}$ で最小値 $\cfrac{1}{\boxed{\text{ ノハ }}}$ をとることがわかる。

解答・解説

ア $4$　イ $2$　ウ $1$　エ $4$

オ $1$　カ $4$　キ $2$　ク $1$　ケ $4$

コサ $16$　シ $4$　ス $4$　セ $3$　ソ $4$

タ,チ,ツ $2,4,3$　テ,ト,ナ $6,4,3$

ニ $1$　ヌ $6$　ネ $2$　ノハ $12$

$C:y=x^2$

$x$ で微分して

$y’=2x$

これが接線の傾きを表すので，直線の方程式を求めると

$\begin{aligned}\ell:&y-a^2=2a(x-a)\\&y=2ax-a^2\end{aligned}$

$a$ を $b$ に置き換えれば $m$ の式となる。

$m:y=2bx-b^2$

また，垂直な 2 直線の傾きの積は $-1$ であるから

$2a\cdot2b=-1$

$4ab=-1$

よって $b=-\cfrac{1}{4a}$

交点 R の座標を求めるために，$\ell$ と $m$ を連立すると

$2ax-a^2=2bx-b^2$

$2(a-b)x=a^2-b^2$

$2(a-b)x=(a+b)(a-b)$

$2x=a+b$

$x=\cfrac{1}{2}\bigg(a-\cfrac{1}{4a}\bigg)$

これを $\ell$ に代入して

$y=2a\cdot\cfrac{1}{2}\bigg(a-\cfrac{1}{4a}\bigg)-a^2$

$=a^2-\cfrac{1}{4}-a^2=-\cfrac{1}{4}$

したがって

R $\bigg(\cfrac{1}{2}\bigg(a-\cfrac{1}{4a}\bigg),\space-\cfrac{1}{4}\bigg)$

次に交点 T の座標を求める

直線 $\ell$ に垂直な直線の傾きは $-\cfrac{1}{2a}$ だから

$\begin{aligned}\ell’:y&-a^2=-\cfrac{1}{2a}(x-a)\\y&=-\cfrac{1}{2a}x+a^2+\cfrac{1}{2}\end{aligned}$

$m’:y=-\cfrac{1}{2b}x+b^2+\cfrac{1}{2}$

ここで $a$ と $b$ の関係式は

$-\cfrac{1}{2a}\bigg(-\cfrac{1}{2b}\bigg)=-1$

$\cfrac{1}{4ab}=-1$

$-4ab=1$

$b=-\cfrac{1}{4a}$

$\ell’$ と $m’$ を連立すると

$-\cfrac{1}{2a}x+a^2+\cfrac{1}{2}=-\cfrac{1}{2b}x+b^2+\cfrac{1}{2}$

$\cfrac{1}{2a}x-a^2=\cfrac{1}{2ab}x-b^2$

$\bigg(\cfrac{1}{2a}-\cfrac{1}{2b}\bigg)x=a^2-b^2$

$\cfrac{1}{2}\bigg(\cfrac{1}{a}-\cfrac{1}{b}\bigg)x=(a+b)(a-b)$

$\cfrac{1}{2}\cdot\cfrac{b-a}{ab}x=(a+b)(a-b)$

$-\cfrac{1}{2}\cdot\cfrac{a-b}{ab}x=(a+b)(a-b)$

$-\cfrac{1}{2ab}x=a+b$

$x=-2ab(a+b)$

$x=-2a\bigg(-\cfrac{1}{4a}\bigg)\bigg(a-\cfrac{1}{4a}\bigg)$

$=\cfrac{1}{2}\bigg(a-\cfrac{1}{4a}\bigg)$

これを $\ell’$ に代入して

$y=-\cfrac{1}{2a}\cdot\cfrac{1}{2}\bigg(a-\cfrac{1}{4a}\bigg)+a^2+\cfrac{1}{2}$

$=-\cfrac{1}{4}+\cfrac{1}{16a^2}+a^2+\cfrac{1}{2}$

$=a^2+\cfrac{1}{16a^2}+\cfrac{1}{4}$

したがって

T $\bigg(\cfrac{1}{2}\bigg(a-\cfrac{1}{4a}\bigg),\space a^2+\cfrac{1}{16a^2}+\cfrac{1}{4}\bigg)$

点 T の軌跡を求めるには，式変形によって媒介変数である $a$ を消去するとよい。

$\begin{cases}x=\cfrac{1}{2}\bigg(a-\cfrac{1}{4a}\bigg)\\y=a^2+\cfrac{1}{16a^2}+\cfrac{1}{4}\end{cases}$

$x$ の式を 2 乗して

$x^2=\cfrac{1}{4}\bigg(a-\cfrac{1}{4a}\bigg)^2$

$=\cfrac{1}{4}\bigg(a^2-\cfrac{1}{2}+\cfrac{1}{16a^2}\bigg)$

$4x^2=a^2+\cfrac{1}{16a^2}-\cfrac{1}{2}$

$a^2+\cfrac{1}{16a^2}=4x^2+\cfrac{1}{2}$

これを $y$ の式に代入して

$y=4x^2+\cfrac{1}{2}+\cfrac{1}{4}$

$=4x^2+\cfrac{3}{4}$

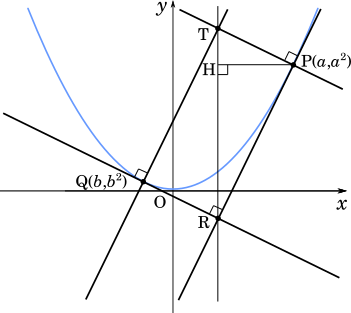
R と T の $x$ 座標が同じであることに注意すると，RT は垂直であることから 2 つの三角形に分けて考えるとよい。

RT = $a^2+\cfrac{1}{16a^2}+\cfrac{1}{4}-\bigg(-\cfrac{1}{4}\bigg)$

$=a^2+\cfrac{1}{16a^2}+\cfrac{1}{2}$

PH = $a-\cfrac{1}{2}\bigg(a-\cfrac{1}{4a}\bigg)$

$=\cfrac{1}{2}a+\cfrac{1}{8a}$

$=\cfrac{1}{2}\bigg(a+\cfrac{1}{4a}\bigg)$

$S_1=2\cdot\cfrac{1}{2}\cdot\cfrac{1}{2}\bigg(a^2+\cfrac{1}{16a^2}+\cfrac{1}{2}\bigg)\bigg(a+\cfrac{1}{4a}\bigg)$

ここで，上の計算式にさかのぼって

$\bigg(a+\cfrac{1}{4a}\bigg)^2=a^2+\cfrac{1}{2}+\cfrac{1}{16a^2}$

であることを利用するとよい。したがって

$S_1=\cfrac{1}{2}\bigg(a+\cfrac{1}{4a}\bigg)^3$

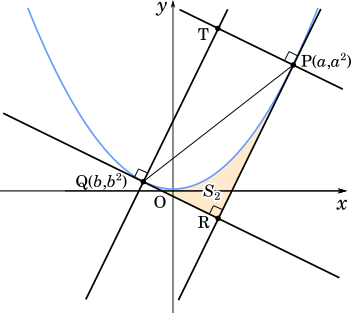
放物線 C と直線 PQ で囲まれた図形の面積は，公式 $\cfrac{|a|}{6}(\beta-\alpha)$ を用いて

$\cfrac{1}{6}(a-b)^3=\cfrac{1}{6}\bigg(a+\cfrac{1}{4a}\bigg)^3$

となる。次に $S_2$ は三角形 PQR から 上で求めた面積を引いたものだから

$S_2=\cfrac{1}{2}\cdot\cfrac{1}{2}\bigg(a+\cfrac{1}{4a}\bigg)^3-\cfrac{1}{6}\bigg(a+\cfrac{1}{4a}\bigg)^3$

$=\bigg(\cfrac{1}{4}-\cfrac{1}{6}\bigg)\bigg(a+\cfrac{1}{4a}\bigg)^3$

$=\cfrac{1}{12}\bigg(a+\cfrac{1}{4a}\bigg)^3$

したがって

$S_2=\cfrac{1}{6}S_1$

また，相加・相乗平均を用いて

$a+\cfrac{1}{4a}\geqq2\sqrt{a\cdot\cfrac{1}{4a}}$

$a+\cfrac{1}{4a}\geqq2\sqrt{\cfrac{1}{4}}$

$a+\cfrac{1}{4a}\geqq2\cdot\cfrac{1}{2}$

$a+\cfrac{1}{4a}\geqq1$

$S_2$ は $a+\cfrac{1}{4a}=1$ で最小値をとる。式を変形して

$4a^2+1=4a$

$4a^2-4a+1=0$

$(2a-1)^2=0$

$a=\cfrac{1}{2}$

したがって $S_2$ は $a=\cfrac{1}{2}$ で最小値 $\cfrac{1}{12}$ をとる。