【スマホで読む・わかりやすい】センター数学IIB2013本試【解説・正解・問題】

第２問

$a$ を正の実数として，$x$ の関数 $f(x)$ を

$f(x)=x^3-3a^2 x+a^3$

とする。

関数 $y=f(x)$ は，$x=\boxed{\text{ アイ }}$ で極大値 $\boxed{\text{ ウ }}\space a^{\boxed{\text{エ}}}$ をとり，$x=\boxed{\text{ オ }}$ で極小値 $\boxed{\text{ カ }}\space a^{\boxed{\text{ キ }}}$ をとる。このとき，2 点

$\bigg(\boxed{\text{ アイ }},\boxed{\text{ ウ }}\space a^{\boxed{\text{ エ }}}\bigg)$，$\bigg(\boxed{\text{ オ }},\boxed{\text{ カ }}\space a^{\boxed{\text{ キ }}}\bigg)$

と原点を通る放物線

$y=\boxed{\text{ ク }}\space x^2-\boxed{\text{ ケ }}\space a^{\boxed{\text{ コ }}} x$

を $C$ とする。原点における $C$ の接線 $\ell$ の方程式は

$y=\boxed{\text{ サシ }}\space a^{\boxed{\text{ス}}} x$

である。また，原点を通り $\ell$ に垂直な直線 $m$ の方程式は

$y=\cfrac{1}{\boxed{\text{ セ }}\space a^{\boxed{\text{ソ}}}} x$
である。

$x$ 軸に関して放物線 $C$ と対称な放物線

$y=-\boxed{\text{ ク }}x^2+\boxed{\text{ ケ }}\space a^{\boxed{\text{コ}}}\space x$

を $D$ とする。 $D$ と $\ell$ で囲まれた図形の面積 $S$ は

$S=\cfrac{\boxed{\text{ タチ }}}{\boxed{\text{ ツ }}}a^{\boxed{\text{テ}}}$

である。

放物線 $C$ と直線 $m$ の交点の $x$ 座標は，$0$ と $\cfrac{4a^{\boxed{\text{ト}}}+1}{2a^{\boxed{\text{ナ}}}}$ である。$C$ と $m$ で囲まれた図形の面積を $T$ とする。$S=T$ となるのは $a^{\boxed{\text{テ}}}=\cfrac{\boxed{\text{ ニ }}}{\boxed{\text{ ヌ }}}$ のときであり，このとき，$S=\cfrac{\boxed{\text{ ネ }}}{\boxed{\text{ ノ }}}$ である。

解答・解説

アイ $-a$　ウ,エ $3,3$　オ $a$

カ,キ $-,3$　ク,ケ,コ $a,2,2$

サシ,ス $-2,2$　セ,ソ $2,2$

タチ,ツ,テ $32,3,4$

ト,ナ $4,3$　ニ,ヌ $1,4$

ネ,ノ $8,3$

$f(x)=x^3-3a^2x+a^3$

$f'(x)=3x^2-3a^2$

$3x^2-3a^2=0$ とおいて

$x^2-a^2=0$

$x^2=a^2$

$x=\pm a$

$\begin{aligned}x&&\cdots&&-a&&\cdots&&a&&\cdots\\f'(x)&&+&&0&&-&&0&&+\\f(x)&&\nearrow&&\text{極大}&&\searrow&&\text{極小}&&\nearrow\end{aligned}$

$f(-a)=(-a)^3-3a^2(-a)+a^3$

$=-a^3+3a^3+a^3$

$=-a^3$

$f(a)=a^3-3a^3+a^3$

$=-a^3$

したがって

$x=-a$ で極大値 $3a^3$

$x=a$ で極小値 $-a^3$

をとる。

次に $(-a,3a^3),(a,-a^3)$ と原点を通る放物線を

$y=bx^2+cx+d$

とおく。

$(0,0)$ を代入して

$d=0$

よって式は $y=bx^2+cx$ と表せる。

$(-a,3a^3)$ を代入して

$3a^3=b(-a)^2+c(-a)$

$3a^3=-ba^2-ca$

$3a^3-ba^2+ca=0$

$(a,-a^3)$ を代入して

$-a^3=ba^2+ca$

$a^3+ba^2+ca=0$

$3a^3-ba^2+ca=0$ と $a^3+ba^2+ca=0$ を連立して 2 つの式を足すと

$4a^3+2ca=0$

$2a^2+c=0$

$c=-2a^2$

これを $a^3+ba^2+ca=0$ に代入して

$a^3+ba^2-2a^3=0$

$-a^3+ba^2=0$

$a-b=0$

$b=a$

したがって

$C:y=ax^2-2a^2x$

また $g(x)=ax^2-2a^2x$ とおくと

$g'(x)=2ax-2a^2$

$g'(0)=-2a^2$

したがって，原点における $C$ の接線の方程式は

$\ell:y=-2a^2x$

$\ell$ に垂直な直線の傾きを $k$ とおくと

$-2a^2k=-1$

$k=\cfrac{1}{2a^2}$

したがって

$m:y=\cfrac{1}{2a^2}x$

次に $D:y=-ax^2+2a^2x$ とする。$x^2$ の係数が負の値なので上に凸のグラフになる。

$\ell$ と $D$ の交点を求めると

$-2a^2x=-ax^2+2a^2x$

$2ax=x^2-2ax$

$x^2-4ax=0$

$x(x-4a)=0$

$x=0,4a$

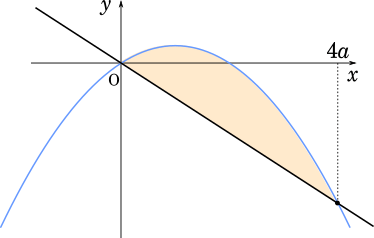
面積 $S$ を $\cfrac{1}{6}$ 公式 $S=\cfrac{|a|(\beta-\alpha)^3}{6}$ を用いて求めると

$S=\cfrac{a(4a-0)^3}{6}$

$=\cfrac{32}{3}a^4$

放物線 $C$ と直線 $m$ の交点の $x$ 座標を求めると，式を連立して

$ax^2-2a^2x=\cfrac{1}{2a^2}x$

$2a^3x^2-4a^4x=x$

$2a^3x-2-(4a^4+1)x=0$

$x(2a^3x-4a^4-1)=0$

$x=0,\cfrac{4a^4+1}{2a^3}$

また，$C$ と $D$ は $x$ 軸対称だから，$\ell$ と $m$ が $x$ 軸対称であれば面積が一致する。

$2a^2=\cfrac{1}{2a^2}$

$4a^4=1$

$a^4=\cfrac{1}{4}$

したがって

$S=\cfrac{32}{3}\cdot\cfrac{1}{4}$

$=\cfrac{8}{3}$