【スマホで読む・わかりやすい】センター数学IIB2012追試【解説・正解・問題】

第4問

OP=$1$，OQ=$2$，∠POQ=$90$° である三角形 OPQ において，線分 OP を $2 :1$ に内分する点を L，線分 OQ を $a :(1 -a)$ に内分する点を M とする。ただし，$0 < a < 1$ とする。さらに，線分 PQ 上に点 N を ∠LMN =$90$° となるようにとる。

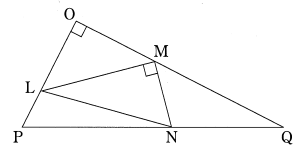
$\overrightarrow{\text{OP}}=\vec{p}$，$\overrightarrow{\text{OQ}}=\vec{q}$ とおき，PN:NQ= $b:(1-b)$ とする。

(1)　$\overrightarrow{\text{ML}}$ と $|\overrightarrow{\text{ML}}|$ は $a$ を用いて

$\overrightarrow{\text{ML}}=\cfrac{\boxed{\text{ ア }}}{\boxed{\text{ イ }}}\vec{p}-\boxed{\text{ ウ }}\vec{q},|\overrightarrow{\text{ML}}|=\cfrac{\boxed{\text{ エ }}}{\boxed{\text{ オ }}}\sqrt{1+\boxed{\text{ カ }}a^2}$

と表される。

(2)　$|\overrightarrow{\text{MN}}|$ を $a$ を用いて表そう。まず，$\overrightarrow{\text{MN}}$ は $a$，$b$ を用いて

$\overrightarrow{\text{MN}}=(1-\boxed{\text{ キ }})\vec{p}+(\boxed{\text{ ク }}-\boxed{\text{ ケ }})\vec{q}$

と表される。$\overrightarrow{\text{ML}}\cdot\overrightarrow{\text{MN}}=\boxed{\text{ コ }}$ であるから， $b=\cfrac{1+\boxed{\text{ サ }}a^2}{\boxed{\text{ シ }}+\boxed{\text{ ス }}a}$である。

したがって，$|\overrightarrow{\text{MN}}|$ は $a$ を用いて

$|\overrightarrow{\text{MN}}|=\cfrac{\boxed{\text{ セ }}(\boxed{\text{ ソ }}-a)}{\boxed{\text{ シ }}+\boxed{\text{ ス }}a}\sqrt{1+\boxed{\text{ タ }}a^2}$

と表される。

(3)　三角形 LMN と三角形 QOP は相似であるとする。直線 OQ と直線 LN の交点を求めよう。

$|\overrightarrow{\text{ML}}|=\boxed{\text{ チ }}|\overrightarrow{\text{MN}}|$ であるから，$a=\cfrac{\boxed{\text{ ツ }}}{\boxed{\text{ テト }}}$，$b=\cfrac{ \boxed{\text{ ナ }}}{\boxed{\text{ ニヌ }} }$ である。$s$ を実数とし，直線 LN 上に点 R を $\overrightarrow{\text{LR}}=s\overrightarrow{\text{LN}}$ となるようにとる。$\overrightarrow{\text{OR}}$ は $s$ を用いて

$\overrightarrow{\text{OR}}=\bigg(\cfrac{\boxed{\text{ ネ }}}{\boxed{\text{ ノ }}}-\cfrac{s}{\boxed{\text{ ハ }}} \bigg)\vec{p}+\cfrac{\boxed{\text{ ナ }}}{\boxed{\text{ ニヌ }}}s\vec{q}$

と表される。$s=\cfrac{\boxed{\text{ ヒ }}}{\boxed{\text{ フ }}}$ のとき， R は，直線 OQ 上の点でもあるので，直線 OQ と直線 LN の交点となる。

解答・解説

ア $2$

イ $3$

ウ $a$

エ $2$

オ $3$

カ $9$

キ,ク,ケ $b,b,a$

コ $0$

サ,シ,ス $6,1,6$

セ,ソ,タ $2,1,9$

チ $2$

ツ $5$

テト $12$

ナ $7$

ニヌ $12$

ネ $2$

ノ $3$

ハ $4$

ヒ $8$

フ $3$

(1)

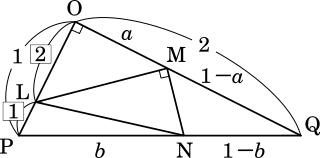
$\overrightarrow{\text{ML}}=\overrightarrow{\text{OL}}-\overrightarrow{\text{OM}}$

$=\cfrac{2}{3}\vec{p}-a\vec{q}$

ベクトルの長さを求めるには，いったん 2 乗した式を作ると良い。

$|\overrightarrow{\text{ML}}|^2=\bigg(\cfrac{2}{3}\vec{p}-a\vec{q}\bigg)^2$

$=\cfrac{4}{9}|\vec{p}|^2-\cfrac{4}{3}a\vec{p}\cdot\vec{q}+a^2|\vec{q}|^2$

$\vec{p}$ と $\vec{q}$ は垂直だから，内積 $\vec{p}\cdot\vec{q}=0$ である。また，$|\vec{p}|=1$，$|\vec{q}|=2$ だから

$=\cfrac{4}{9}+4a^2$

したがって

$|\overrightarrow{\text{ML}}|=\sqrt{\cfrac{4}{9}+4a^2}$

$=2\sqrt{\cfrac{1}{9}+a^2}$

$=2\sqrt{\cfrac{1+9a^2}{9}}$

$=\cfrac{2}{3}\sqrt{1+9a^2}$

(2)

$\overrightarrow{\text{MN}}=\overrightarrow{\text{ON}}-\overrightarrow{\text{OM}}$

例えば，直線 AB を $t:(1-t)$ で内分する点 P は $\vec{p}=(1-t)\vec{a}+t\vec{b}$ と表す。これを用いて

$=(1-b)\vec{p}+b\vec{q}-a\vec{q}$

$=(1-b)\vec{p}+(b-a)\vec{q}$

ML と MN は垂直だから $\overrightarrow{\text{ML}}\cdot\overrightarrow{\text{MN}}=0$

$\overrightarrow{\text{ML}}\cdot\overrightarrow{\text{MN}}=\bigg(\cfrac{2}{3}\vec{p}-a\vec{q}\bigg)\{(1-b)\vec{p}+(b-a)\vec{q}\}$

式を展開して

$=\cfrac{2}{3}(1-b)|\vec{p}|^2+\cfrac{2}{3}(b-a)\vec{p}\cdot\vec{q}-a(1-b)\vec{p}\cdot\vec{q}-a(b-a)|\vec{q}|^2$

$\vec{p}\cdot\vec{q}=0$，$|\vec{p}|=1$，$|\vec{q}|=2$ だから

$=\cfrac{2}{3}(1-b)-4a(b-a)$

$=\cfrac{2}{3}-\cfrac{2}{3}b-4ab+4a^2=0$

両辺を 2 で割って

$\cfrac{1}{3}-\cfrac{1}{3}b-2ab+2a^2=0$

$\bigg(\cfrac{1}{3}+2a\bigg)b=\cfrac{1}{3}+2a^2$

両辺を 3 倍して

$(1+6a)b=1+6a^2$

$b=\cfrac{1+6a^2}{1+6a}$

また

$|\overrightarrow{\text{MN}}|^2=\{(1-b)\vec{p}+(b-a)\vec{q}\}^2$

$=(1-b)^2|\vec{p}|^2+2(1-b)(b-a)\vec{p}\cdot\vec{q}+(b-a)^2|\vec{q}|^2$

$=(1-b)^2+4(b-a)^2$

ここから方針としては，左辺の 2 乗を外す必要があるので，右辺は単項式にしなければならない。このことを意識しながら式変形を行うとよい。

$=\bigg(1-\cfrac{1+6a^2}{1+6a}\bigg)^2+4\bigg(\cfrac{1+6a^2}{1+6a}-a\bigg)^2$

$=\bigg(\cfrac{1+6a-1-6a^2}{1+6a}\bigg)^2+4\bigg(\cfrac{1+6a^2-a-6a^2}{1+6a}\bigg)^2$

$=\bigg(\cfrac{6a-6a^2}{1+6a}\bigg)^2+4\bigg(\cfrac{1-a}{1+6a}\bigg)^2$

$=(6a)^2\bigg(\cfrac{1-a}{1+6a}\bigg)^2+4\bigg(\cfrac{1-a}{1+6a}\bigg)^2$

$=\bigg(\cfrac{1-a}{1+6a}\bigg)^2(36a^2+4)$

$=4\bigg(\cfrac{1-a}{1+6a}\bigg)^2(9a^2+1)$

したがって

$|\overrightarrow{\text{MN}}|=\cfrac{2(1-a)}{1+6a}\sqrt{1+9a^2}$

(3)

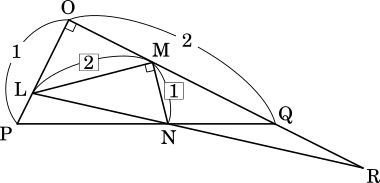
△LMN ∽ △QOP だから

MN : ML = OP : OQ = 1 : 2

したがって

$|\overrightarrow{\text{ML}}|=2|\overrightarrow{\text{MN}}|$

上で求めた式を代入すると

$\cfrac{2}{3}\sqrt{1+9a^2}=2\cfrac{2(1-a)}{1+6a}\sqrt{1+9a^2}$

$\cfrac{1}{3}=\cfrac{2(1-a)}{1+6a}$

$1+6a=6(1-a)$

$1+6a=6-6a$

$12a=5$

$a=\cfrac{5}{12}$

また

$b=\cfrac{1+6\bigg(\cfrac{5}{12}\bigg)^2}{1+6\cfrac{5}{12}}$

$=\cfrac{1+\cfrac{150}{144}}{1+\cfrac{5}{2}}$

$=\cfrac{7}{12}$

次に，$\overrightarrow{\text{OR}}$ を求めると

$\overrightarrow{\text{OR}}=\overrightarrow{\text{OL}}+\overrightarrow{\text{LR}}$

$=\overrightarrow{\text{OL}}+s\overrightarrow{\text{LN}}$

$=\cfrac{2}{3}\vec{p}+s(\overrightarrow{\text{ON}}-\overrightarrow{\text{OL}})$

$=\cfrac{2}{3}\vec{p}+s\bigg\{(1-b)\vec{p}+b\vec{q}-\cfrac{2}{3}\vec{p}\bigg\}$

$=\cfrac{2}{3}\vec{p}+s\bigg\{\bigg(\cfrac{1}{3}-b\bigg)\vec{p}+b\vec{q}\bigg\}$

$=\cfrac{2}{3}\vec{p}+\cfrac{1}{3}s\vec{p}-bs\vec{p}+bs\vec{q}$

$=\bigg(\cfrac{2}{3}+\cfrac{1}{3}s-bs\bigg)\vec{p}+bs\vec{q}$

$=\bigg(\cfrac{2}{3}+\cfrac{1}{3}s-\cfrac{7}{12}s\bigg)\vec{p}+\cfrac{7}{12}s\vec{q}$

$=\bigg(\cfrac{2}{3}-\cfrac{s}{4}\bigg)\vec{p}+\cfrac{7}{12}s\vec{q}$

OR は OQ の延長線上，つまり平行だから

$\cfrac{2}{3}-\cfrac{s}{4}=0$

である。したがって

$\cfrac{2}{3}=\cfrac{s}{4}$

$s=\cfrac{8}{3}$