【スマホで読む・わかりやすい】センター数学IIB2012追試【解説・正解・問題】
第2問
座標平面上で,放物線 $y=x^2+2x-3$ を $C$ とする。
$C$ 上の点 $(a,\space a^2+2a-3)$ における $C$ の接線の方程式は
$y=(\boxed{\text{ アイ }}+\boxed{\text{ ウ }})x-a^{\boxed{\text{エ}}}-\boxed{\text{ オ }}$
である。特に,$a=0$ のときの接線の方程式は$y=\boxed{\text{ カ }}x-\boxed{\text{ キ }}\cdots$①
となる。
実数 $b$,$c$ は $b < 0 < c$ を満たすとする。放物線 $C$ と接線 ①,および2直線 $x=b$,$x=c$ で囲まれた二つの部分の面積の和 $S$ は
$S=\cfrac{1}{\boxed{\text{ ク }}}\bigg(\boxed{\text{ ケ }}^{\boxed{\text{ コ }}}-\boxed{\text{ サ }}^{\boxed{\text{ コ }}} \bigg)$
である。
$0$ 以上の実数 $t$ を用いて,$b$ と $c$ を
$b=- | t-1| -4$,$c=4t+1$
とおくことにする。このとき,$S$ を $t$ を用いて表し,$t$ の値が変化するときの $S$ の最小値を求めよう。
$0\leqq t \leqq 1$ のとき
$S=\cfrac{1}{\boxed{\text{ ク }}}\bigg\{(\boxed{\text{ シ }}t+\boxed{\text{ ス }})^{\boxed{\text{ コ }}}-(t-\boxed{\text{ セ }})^{\boxed{\text{ コ }}}\bigg\}$
となり,$t > 1$ のとき
$S=\cfrac{1}{\boxed{\text{ ク }}}\bigg\{(\boxed{\text{ シ }}t+\boxed{\text{ ス }})^{\boxed{\text{ コ }}}+(t-\boxed{\text{ ソ }})^{\boxed{\text{ コ }}}\bigg\}$
となる。
$0 \leqq t \leqq 1$ のとき,$S$ の増減を調べると,$S$ は
$t=\cfrac{\boxed{\text{ タ }}}{\boxed{\text{ チ }}}$
で最小値をもつことがわかる。
$t > 1$ のとき,$t$ の値が増加すると,$S$ は $\boxed{\text{ ツ }}$ することがわかる。$\boxed{\text{ ツ }}$ に当てはまるものを,次の ⓪ ~ ③ のうちから一つ選べ。
⓪ 減少 ① 減少してから増加 ② 増加 ③ 増加してから減少
以上により,$t \geqq 0$ における $S$ の最小値は
$\cfrac{\boxed{\text{ テトナ }}}{\boxed{\text{ ニ }}}$
である。
解説・解説
アイ,ウ $2a$,$2$
エ,オ $2,3$
カ,キ $2,3$
ク,ケ,コ,サ $3,c,3,b$
シ $4$
ス $1$
セ $5$
ソ $3$
タ $1$
チ $3$
ツ $2$
テトナ $343$
ニ $9$
$f(x)=x^2+2x-3$ として $x$ で微分すると
$f'(x)=2x+2$
$x=a$ における接線の傾きは$f'(a)=2a+2$ だから,接線の方程式は
$y-(a^2+2a-3)=(2a+2)(x-a)\\y=(2a+2)x-(2a+2)a+a^2+2a-3\\y=(2a+2)x-a^2-3$
$a=0$ のとき $y=2x-3$
$f(x)$ を平方完成すると
$f(x)=x^2+2x-3\\=(x+1)^2-1-3\\=(x+1)^2-4$
したがって,頂点の座標は $(-1,-4)$
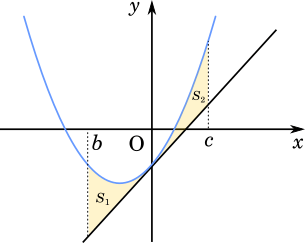
積分区間が連続しているので $S_1$ と $S_2$ の式は 1 つにまとめることができる
$\displaystyle S=\int_b^c x^2+2x-3-2x+3\space dx\\\displaystyle=\int_b^c x^2\space dx\\=\bigg[\cfrac{x^3}{2}\bigg]_b^c\\=\cfrac{c^3}{3}-\cfrac{b^3}{b}\\=\cfrac{1}{3}(c^3-b^3)$
次に $b=-|t-1|-4$,$c=4t+1$ とおいて
$0\leqq t\leqq 1$ のとき
$t-1$ は負の値になるから,$b$ の絶対値の符号を外すと
$b=-(-t+1)-4\\=t-1-4\\=t-5$
これより
$S=\cfrac{1}{3}\{(4t+1)^3-(t-5)^3\}$
$t > 1$ のとき
$t-1$ は正の値になるから,$b$ の絶対値の符号を外すと
$b=-(t-1)-4\\=-t+1-4\\=-t-3\\=-(t+3)$
ここで,$b=-(t+3)$ を $b=(-1)(t+3)$ とすると,$b^3=(-1)^3(t+3)^3=(-1)(t+3)^3=-(t+3)^3$ となる。したがって
$S=\cfrac{1}{3}\{(4t+1)^3+(t+3)^3\}$
$0\leqq t\leqq 1$ のとき
$S=\cfrac{1}{3}\{(4t+1)^3-(t-5)^3\}$ の増減を調べる。まず,式を整理して$x$ で微分した上で増減表を作るとよい。
$(4t+1)^3=64t^3+48t^2+12t+1$
$(t-5)^3=t^3-15t^2+75t-125$
引き算して
$63t^3+63t^2-63t+126$
$=63(t^3+t^2-t+2)$
面積を $S(t)$ とおくと
$S(t)=\cfrac{1}{3}\cdot63(t^3+t^2-t+2)\\=21(t^3+t^2-t+2)\\S'(t)=21(3t^2+2t-1)$
$S'(t)=0$ とおくと
$21(3t^2+2t-1)=0$
$3t^2+2t-1=0$
$(3t-1)(t+1)=0$
$t=-1,\cfrac{1}{3}$
| $t$ | $\cdots$ | $-1$ | $\cdots$ | $\cfrac{1}{3}$ | $\cdots$ |
| $S'(t)$ | $+$ | $0$ | $-$ | $0$ | $+$ |
| $S(t)$ | $\nearrow$ | 最大 | $\searrow$ | 最小 | $\nearrow$ |
したがって,$S$ は $\cfrac{1}{3}$ で最小値をもつ。
$t > 1$ のとき $S(t)$ について考えると,$t$ が増加すると $4t+1$ は増加し,$t+3$ も増加する。したがって $S$ は増加することがわかる。
したがって,$t$ 全体で考えても,$S(t)$ は $t=\cfrac{1}{3}$ で最小値をとる。
$S\bigg(\cfrac{1}{3}\bigg)=21\bigg(\cfrac{1}{27}+\cfrac{1}{9}-\cfrac{1}{3}+2\bigg)$
$=\cfrac{21(1+3-9+54)}{27}$
$=\cfrac{343}{9}$
SNSでシェア