【スマホで読む・わかりやすい】センター数学IIB2012追試【解説・正解・問題】

第1問

〔1〕　不等式
$\log_3 (x^2 -2x ) < 1 \cdots$①
を満たす $x$ に対して
$u=\log_2 ( 2x^2 +2x+1)$
とおく。$u$ の値が整数となる $x$ と，そのときの $u$ の値を求めよう。
真数は正であることに注意して，不等式①を満たす $x$ のとり得る値の範囲を求めると
$-\boxed{\text{ ア }} < x < \boxed{\text{ イ }}$，$\boxed{\text{ ウ }} < x < \boxed{\text{ エ }}$
となる。ただし，対数 $\log_a b$ に対し，$a$ を底といい，$b$ を真数という。
$\boxed{\text{ ウ }} < x < \boxed{\text{ エ }}$ のとき， $2x^2+2x+1$ のとり得る値の範囲を考えると，$u$ の値が整数となるのは
$2x^2+2x+1=\boxed{\text{ オカ }}\cdots$②
となる場合であり，このとき，$u= \boxed{\text{ キ }}$ である。また，$\boxed{\text{ ウ }} < x < \boxed{\text{ エ }}$ を満たす方程式②の解は
$x=\cfrac{-1+\sqrt{\boxed{\text{ クケ }}}}{2}$
である。
同様に，$-\boxed{\text{ ア }} < x < \boxed{\text{ イ }}$ のとき，$u$ の値が整数となるのは
$2x^2+2x+1=\cfrac{\boxed{\text{ コ }}}{\boxed{\text{ サ }}}\cdots$③
となる場合であり，このとき，$u=\boxed{\text{ シス }}$ である。また，$-\boxed{\text{ ア }} < x < \boxed{\text{ イ }}$ を満たす方程式③の解は $x=\cfrac{\boxed{\text{ セソ }}}{\boxed{\text{ タ }}}$ である。

〔2〕

関数
$f(x)=x^2+4\bigg(\cfrac{3\tan\theta}{1+\tan^2\theta} -\sqrt{3}\bigg)x+3\bigg(\sin^2\theta+3\cos^2\theta\bigg)^2$
について，すべての実数 $x$ に対して $f(x) > 0$ が成り立つような $\theta$ の値の範囲を求めよう。ただし， $-\cfrac{\pi}{2} < \theta < \cfrac{\pi}{2}$ とする。
不等式 $f(x) > 0$ がすべての実数 $x$ に対して成り立つための条件は， 2次方程式 $f(x)=0$ の判別式 $D$ が $D \boxed{\text{ チ }} 0$ を満たすことである。$\boxed{\text{ チ }}$ に当てはまるものを，次の ⓪ ～ ② のうちから一つ選べ。

⓪ $<$　① $=$　② $>$

2倍角の公式により
$\sin^2\theta+3\cos^2\theta=\boxed{\text{ ツ }}+\cos2\theta$
$\cfrac{3\tan\theta}{1+\tan^2\theta}=\cfrac{\boxed{\text{ テ }}}{\boxed{\text{ ト }}}\sin2\theta$
であるから，判別式 $D$ は
$D=12(\boxed{\text{ ナ }}\sin2\theta+\cos2\theta)(\sqrt{\boxed{\text{ ナ }}}\sin 2\theta-\cos 2\theta-\boxed{\text{ ニ }})$
と表すことができる。
ここで
$\sqrt{\boxed{\text{ ナ }}}\sin2\theta-\cos2\theta-\boxed{\text{ ニ }}\space\boxed{\text{ ヌ }} 0$
である。$\boxed{\text{ ヌ }}$ に当てはまるものを，次の ⓪ ～ ② のうちから一つ選べ。

⓪ $ < $　① $=$　② $ > $

また
$\sqrt{\boxed{\text{ナ}}}\sin2\theta+\cos2\theta=\boxed{\text{ ネ }}\sin\bigg(2\theta+\cfrac{\pi}{\boxed{\text{ ノ }}}\bigg)$
であるから，条件 D $\boxed{\text{ チ }} 0$ により，不等式 $f(x) > 0$ がすべての実数 $x$ に対して成り立つような $\theta$ のとり得る値の範囲は
$-\cfrac{\pi}{\boxed{\text{ ハヒ }}} < \theta < \cfrac{\boxed{ フ }}{\boxed{\text{ ハヒ }}}\pi$
であることがわかる。

解答・解説

ア $1$

イ $0$

ウ $2$

エ $3$

オカ $16$

キ $4$

クケ $31$

コ $1$

サ $2$

シス $-1$

セソ $-1$

タ $2$

チ $0$

ツ $2$

テ $3$

ト $2$

ナ,ニ $3,4$

ヌ $0$

ネ $2$

ノ $6$

ハヒ,フ $12,5$

〔1〕
真数条件より
$x^2-2x > 0\\x(x-2) > 0\\x < 0,\space 2 < x$
また，$\log_3 (x^2-2x)=1$ とおくと
$3^1=x^2-2x$
となるので
$x^2-2x < 3$
が成り立つ。式を変形して
$x^2-2x-3 < 0$
$(x-3)(x+1) < 0$
$-1 < x < 3$
これと
$x^2-2x > 0\\x(x-2) > 0\\x < 0,\space 2 < x$
を重ねると
$-1 < x < 0,\space 2 < x < 3$

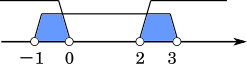
$2 < x < 3$ のとき, $u$ が整数となる場合を考える。
$u=\log_2 (2x^2+2x+1)$ は $2^u=2x^2+2x+1$ と変形できる。
$2x^2+2x+1$ を平方完成して
$=2(x^2+x)+1\\=2\bigg(x+\cfrac{1}{2}\bigg)^2-\cfrac{2}{4}+1\\=2\bigg(x+\cfrac{1}{2}\bigg)^2+\cfrac{1}{2}$

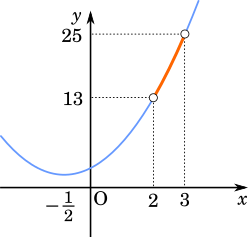
$x=2$ のとき
$2x^2+2x+1=13$
$x=3$ のとき
$2x^2+2x+1=25$
したがって，$13 < 2^u < 25$ である。これに当てはまる整数 $u$ は $4$ である。
$4=\log_2 (2x^2+2x+1)\\2^4=2x^2+2x+1\\2x^2+2x+1=16$
方程式の解を求めると
$2x^2+2x+1=16\\2x^2+2x-15=0\\x=\cfrac{-1\pm\sqrt{1+30}}{2}\\x=\cfrac{-1\pm\sqrt{31}}{2}$

同様に，$-1 < x < 0$ のとき

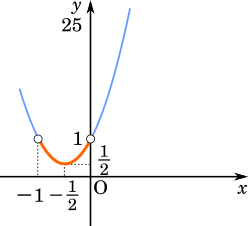
$2^{-1}=\cfrac{1}{2}$ となるので，$u=-1$ が適する。 したがって，方程式③は $2x^2+2x+1=\cfrac{1}{2}$ となり，解を求めると
$2x^2+2x+\cfrac{1}{2}=0\\4x^2+4x+1=0\\x=\cfrac{-2\pm\sqrt{4-4}}{4}\\x=\cfrac{-2}{4}$

〔2〕

不等式 $f(x) > 0$ がすべての実数 $x$ に対して成り立つための条件は，判別式 $D$ が $D < 0$ を満たすことである。
$\sin^2\theta+3\cos^2\theta$ を変形すると
$=\sin^2\theta+\cos^2\theta+2\cos^2\theta\\=1+2\cos^2\theta$
$\cos\theta$ の2倍角の公式は $\cos^2\theta-\sin^2\theta$ であり，これを変形するとよい
$\cos2\theta=\cos^2\theta-\sin^2\theta\\=\cos^2\theta-(1-\cos^2\theta)\\=2\cos^2\theta-1$
これを用いて
$2\cos^2\theta=\cos2\theta+1\\1+2\cos^2\theta=2+\cos2\theta$
したがって
$\sin^2\theta+3\cos^2\theta=2+\cos2\theta$
また
$\cfrac{3\tan\theta}{1+\tan^2\theta}=\cfrac{3\cfrac{\sin\theta}{\cos\theta}}{\cfrac{1}{\cos^2\theta}}\\=\cfrac{3\sin\theta\cos^2\theta}{\cos\theta}\\=3\sin\theta\cos\theta$
2倍角の公式 $\sin2\theta=2\sin\theta\cos\theta$ より
$\sin\theta\cos\theta=\cfrac{\sin2\theta}{2}$
したがって
$\cfrac{3\tan\theta}{1+\tan^2\theta}=\cfrac{3}{2}\sin2\theta$
これより，$f(x)$ は
$f(x)=x^2+4\bigg(\cfrac{3}{2}\sin2\theta-\sqrt{3}\bigg)x+3(2+\cos2\theta)^2$
となり，判別式 $D$ は
$D=16(\cfrac{3}{2}\sin2\theta-\sqrt{3})^2-12(2+\cos2\theta)^2\\=12\bigg\{\cfrac{4}{3}\bigg(\cfrac{3}{2}\sin2\theta-\sqrt{3}\bigg)^2-(2+\cos2\theta)^2\bigg\}\\=12\bigg\{\bigg(\sqrt{\cfrac{4}{3}}\bigg)^2\bigg(\cfrac{3}{2}\sin2\theta-\sqrt{3}\bigg)^2-(2+\cos2\theta)^2\bigg\}\\=12\bigg\{\bigg(\cfrac{2\sqrt{3}}{3}\bigg)^2\bigg(\cfrac{3}{2}\sin2\theta-\sqrt{3}\bigg)^2-(2+\cos2\theta)^2\bigg\}\\=12\bigg\{\bigg(\cfrac{2\sqrt{3}}{3}\cdot\cfrac{3}{2}\sin2\theta-\cfrac{2\sqrt{3}}{3}\cdot\sqrt{3}\bigg)^2-(2+\cos2\theta)^2\bigg\}\\=12\{(\sqrt{3}\sin2\theta-2)^2-(2+\cos2\theta)^2\}\\=12(\sqrt{3}\sin2\theta-2+2+\cos2\theta)(\sqrt{3}\sin2\theta-2-2-\cos2\theta)\\=12(\sqrt{3}\sin2\theta+\cos2\theta)(\sqrt{3}\sin2\theta-\cos2\theta-4)$
ここで，$\sqrt{3}\sin2\theta-\cos2\theta-4$ を変形すると，三角関数の合成を用いて
$\sqrt{3}\sin2\theta-\cos2\theta-4\\=2\sin\bigg(2\theta-\cfrac{\pi}{6}\bigg)-4$

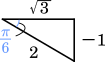
$-\cfrac{\pi}{2} < \theta < \cfrac{\pi}{2}$ だから
$-\pi < 2\theta < \pi\\-\cfrac{7}{6}\pi\leqq 2\theta-\cfrac{\pi}{6} \leqq \cfrac{5}{6}\pi$
これより $\sin$ の値は $-1$ から $1$ の間を取ることが分かる
$-1\leqq\sin\bigg(2\theta-\cfrac{\pi}{6}\bigg)\leqq1\\-2\leqq2\sin\bigg(2\theta-\cfrac{\pi}{6}\bigg)\leqq 2\\-6\leqq 2\sin\bigg(2\theta-\cfrac{\pi}{6}\bigg)-4\leqq -2$
したがって
$\sqrt{3}\sin2\theta-\cos2\theta-4 < 0$
同様に三角関数の合成を用いて
$\sqrt{3}\sin2\theta+\cos2\theta=2\sin\bigg(2\theta+\cfrac{\pi}{6}\bigg)$

条件 $D < 0$ から，$f(x) > 0$ がすべての実数 $x$ に対して成り立つようにするには，(正の数)×(負の数)=(正の数) であることを用いて
$2\sin\bigg(2\theta+\cfrac{\pi}{6}\bigg) > 0$
であればよい。
$\sin\bigg(2\theta+\cfrac{\pi}{6}\bigg) > 0\\0 < 2\theta+\cfrac{\pi}{6} < \pi\\-\cfrac{\pi}{6} < 2\theta < \cfrac{5}{6}\pi\\-\cfrac{\pi}{12} < \theta < \cfrac{5}{12}\pi$