【スマホで読む・わかりやすい】センター数学IIB2012本試【解説・正解・問題】
第4問
空間に異なる 4 点 O,A,B,C を,$\overrightarrow{\text{OA}}$⊥$\overrightarrow{\text{OB}}$,$\overrightarrow{\text{OB}}$⊥$\overrightarrow{\text{OC}}$,$\overrightarrow{\text{OC}}$⊥$\overrightarrow{\text{OA}}$ となるようにとり,$\overrightarrow{\text{OA}}=\vec{a}$,$\overrightarrow{\text{OB}}=\vec{b}$,$\overrightarrow{\text{OC}}=\vec{c}$ とおく。さらに,3点 D,E,F を,$\overrightarrow{\text{OD}}=\vec{a}+\vec{b}$,$\overrightarrow{\text{OE}}=\vec{b}+\vec{c}$,$\overrightarrow{\text{OF}}=\vec{a}+\vec{c}$ となるようにとり,線分 BD の中点を L,線分 CE の中点を M とし,線分 AD を $3:1$ に内分する点を N とする。
(1) $\overrightarrow{\text{OM}}$,$\overrightarrow{\text{ON}}$ は,$\vec{a}$,$\vec{b}$,$\vec{c}$ を用いて
$\overrightarrow{\text{OM}}=\cfrac{1}{\boxed{\text{ ア }}}\vec{b}+\vec{c}$,$\overrightarrow{\text{ON}}=\vec{a}+\cfrac{\boxed{\text{ イ }}}{\boxed{\text{ ウ }}}\vec{b}$
と表される。
(2) 2 直線 FL,MN が交わることを確かめよう。$0 < s < 1$ とし,線分 FL を $s:(1-s)$ に内分する点を P とする。$\overrightarrow{\text{OP}}$ は,$s$ と $\vec{a}$,$\vec{b}$,$\vec{c}$ を用いて
$\overrightarrow{\text{OP}}=\bigg(\boxed{\text{ エ }}-\cfrac{s}{\boxed{\text{ オ }}}\bigg)\vec{a}+s\vec{b}+(\boxed{\text{ カ }}-s)\vec{c}$
と表される。$s=\cfrac{\boxed{\text{ キ }}}{\boxed{\text{ ク }}}$ のとき,$\overrightarrow{\text{MP}}=\cfrac{\boxed{\text{ ケ }}}{\boxed{\text{ コ }}}\overrightarrow{\text{MN}}$ となるので,M,N,P は一直線上にある。よって,2 直線 FL,MN は交わることがわかる。
(3) 2 直線 FL,MN の交点を G とする。$\overrightarrow{\text{OG}}$,$\overrightarrow{\text{GF}}$ は,$\vec{a}$,$\vec{b}$,$\vec{c}$ を用いて
$\overrightarrow{\text{OG}}=\cfrac{\boxed{\text{ サ }}}{\boxed{\text{ シ }}}(\boxed{\text{ ス }}\vec{a}+\boxed{\text{ セ }}\vec{b}+\vec{c})$
$\overrightarrow{\text{GF}}=\cfrac{\boxed{\text{ サ }}}{\boxed{\text{ シ }}}(\vec{a}-\boxed{\text{ セ }}\vec{b}+\boxed{\text{ ソ }}\vec{c})$
と表される。
$|\vec{a}|=\sqrt{5}$,$|\vec{b}|=4$,$|\vec{c}|=\sqrt{3}$ とする。このとき,$|\overrightarrow{\text{GF}}|=\boxed{\text{ タ }}$,$|\overrightarrow{\text{GM}}|=2$ となる。
次に,直線 OC 上に点 H をとり,実数 $t$ を用いて,$\overrightarrow{\text{OH}}=t\vec{c}$ と表す。$\overrightarrow{\text{GF}}\cdot\overrightarrow{\text{GH}}$,$\overrightarrow{\text{GM}}\cdot\overrightarrow{\text{GH}}$ は,$t$ を用いて
$\overrightarrow{\text{GF}}\cdot\overrightarrow{\text{GH}}=\boxed{\text{ チ }}t+\cfrac{\boxed{\text{ ツテ }}}{\boxed{\text{ ト }}}$…①
$\overrightarrow{\text{GM}}\cdot\overrightarrow{\text{GH}}=2t+\cfrac{10}{3}$…②
と表される。
さらに,∠FGH=∠MGH とする。このときの $t$ の値を求めよう。
$|\overrightarrow{\text{GF}}|=\boxed{\text{ タ }}$,$|\overrightarrow{\text{GM}}|=2$ と ∠FGH=∠MGH であることから
$\overrightarrow{\text{GF}}\cdot\overrightarrow{\text{GH}}=\cfrac{\boxed{\text{ ナ }}}{\boxed{\text{ ニ }}}\overrightarrow{\text{GM}}\cdot\overrightarrow{\text{GH}}$…③
が成り立つ。①,②,③ から,$t=\cfrac{\boxed{\text{ ヌ }}}{\boxed{\text{ ネ }}}$ である。
正解と解説
ア 2
$\cfrac{\text{イ}}{\text{ウ}}$ $\cfrac{3}{4}$
エ,オ,カ $1,2,1$
$\cfrac{\text{キ}}{\text{ク}}$ $\cfrac{2}{3}$
$\cfrac{\text{ケ}}{\text{コ}}$ $\cfrac{2}{3}$
$\cfrac{\text{サ}}{\text{シ}}$,ス,セ $\cfrac{1}{3},2,2$
ソ 2
タ 3
チ,$\cfrac{\text{ツテ}}{\text{ト}}$ $2,\cfrac{16}{3}$
$\cfrac{\text{ナ}}{\text{ニ}}$ $\cfrac{3}{2}$
$\cfrac{\text{ヌ}}{\text{ネ}}$ $\cfrac{1}{3}$
(1)
点 M は 線分 CE の中点だから
$\overrightarrow{\text{OM}}=\cfrac{1}{2}\overrightarrow{\text{OC}}+\cfrac{1}{2}\overrightarrow{\text{OE}}$
$=\cfrac{1}{2}\vec{c}+\cfrac{1}{2}(\vec{b}+\vec{c})$
$=\cfrac{1}{2}\vec{b}+\vec{c}$
点 N は線分 AD を $3:1$ に内分する点だから
$\overrightarrow{\text{ON}}=\cfrac{\overrightarrow{\text{OA}}+3\overrightarrow{\text{OD}}}{3+1}$
$=\cfrac{\vec{a}+3(\vec{a}+\vec{b})}{4}$
$=\vec{a}+\cfrac{3}{4}\vec{b}$
(2)
点 P は線分 FL を $s:(1-s)$ に内分する点だから
$\overrightarrow{\text{OP}}=(1-s)\overrightarrow{\text{OF}}+s\overrightarrow{\text{OL}}$
ここで $\overrightarrow{\text{OL}}$ を求めると,点 L は線分 BD の中点だから
$\overrightarrow{\text{OL}}=\cfrac{1}{2}\overrightarrow{\text{OB}}+\cfrac{1}{2}\overrightarrow{\text{OD}}$
$=\cfrac{1}{2}\vec{b}+\cfrac{1}{2}(\vec{a}+\vec{b})$
$=\cfrac{1}{2}\vec{a}+\vec{b}$
したがって
$\overrightarrow{\text{OP}}=(1-s)(\vec{a}+\vec{c})+s\bigg(\cfrac{1}{2}\vec{a}+\vec{b}\bigg)$
$=(1-s)\vec{a}+(1-s)\vec{c}+\cfrac{1}{2}s\vec{a}+s\vec{b}$
$=\bigg(1-\cfrac{1}{2}s\bigg)\vec{a}+s\vec{b}+(1-s)\vec{c}$
次に,M,N,P が一直線上にあることを示す。
$\overrightarrow{\text{MP}}=k\overrightarrow{\text{MN}}$ とおき,実数 $k$ の値を求める。
$\overrightarrow{\text{MP}}=\overrightarrow{\text{OP}}-\overrightarrow{\text{OM}}$
$=\bigg(1-\cfrac{1}{2}s\bigg)\vec{a}+s\vec{b}+(1-s)\vec{c}-\cfrac{1}{2}\vec{b}-\vec{c}$
$=\bigg(1-\cfrac{1}{2}s\bigg)\vec{a}+\bigg(s-\cfrac{1}{2}\bigg)\vec{b}-s\vec{c}$
$\overrightarrow{\text{MN}}=\overrightarrow{\text{ON}}-\overrightarrow{\text{OM}}$
$=\vec{a}+\cfrac{3}{4}\vec{b}-\cfrac{1}{2}\vec{b}-\vec{c}$
$=\vec{a}+\cfrac{1}{4}\vec{b}-\vec{c}$
$k\overrightarrow{\text{MN}}=k\vec{a}+\cfrac{1}{4}k\vec{b}-k\vec{c}$
これと $\overrightarrow{\text{MP}}$ を比べると
$\begin{cases}k=1-\cfrac{1}{2}s\\\cfrac{1}{4}k=s-\cfrac{1}{2}\\-k=-s\end{cases}$
となる。ここから
$k=s$
$s=1-\cfrac{1}{2}s$
$s=\cfrac{2}{3}$
よって $k=\cfrac{2}{3}$
したがって,$s=\cfrac{2}{3}$ のとき,$\overrightarrow{\text{MP}}=\cfrac{2}{3}\overrightarrow{\text{MN}}$ となるので,M,N,P は一直線上にある。
(3)
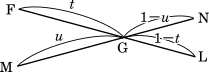
上の図のように FG : GL を $t:(1-t)$,MG : GN を $u:(1-u)$ とおくと
$\overrightarrow{\text{OG}}=(1-s)\overrightarrow{\text{OF}}+t\overrightarrow{\text{OL}}$
$=(1-t)(\vec{a}+\vec{c})+t\bigg(\cfrac{1}{2}\vec{a}+\vec{b}\bigg)$
$=(1-t)\vec{a}+(1-t)\vec{c}+\cfrac{1}{2}t\vec{a}+t\vec{b}$
$=\bigg(1-\cfrac{1}{2}t\bigg)\vec{a}+t\vec{b}+(1-t)\vec{c}$
また
$\overrightarrow{\text{OG}}=(1-u)\overrightarrow{\text{OM}}+u\overrightarrow{\text{ON}}$
$=(1-u)\bigg(\cfrac{1}{2}\vec{b}+\vec{c}\bigg)+u\bigg(\vec{a}+\cfrac{3}{4}\vec{b}\bigg)$
$=\cfrac{1}{2}(1-u)\vec{b}+(1-u)\vec{c}+u\vec{a}+\cfrac{3}{4}u\vec{b}$
$=u\vec{a}+\bigg(\cfrac{1}{2}+\cfrac{1}{4}u\bigg)\vec{b}+(1-u)\vec{c}$
式を比べると
$\begin{cases}1-\cfrac{1}{2}t=u\\t=\cfrac{1}{2}+\cfrac{1}{4}u\\1-t=1-u\end{cases}$
これを解いて,$t=\cfrac{2}{3}$
もとの式に代入すると
$\overrightarrow{\text{OG}}=\bigg(1-\cfrac{1}{2}\cdot\cfrac{2}{3}\bigg)\vec{a}+\cfrac{2}{3}\vec{b}+\bigg(1-\cfrac{2}{3}\bigg)\vec{c}$
$=\cfrac{1}{3}(2\vec{a}+2\vec{b}+\vec{c})$
次に,$\overrightarrow{\text{GF}}$ を求めると
$\overrightarrow{\text{GF}}=\overrightarrow{\text{OF}}-\overrightarrow{\text{OG}}$
$=\vec{a}+\vec{c}-\cfrac{1}{3}(2\vec{a}+2\vec{b}+\vec{c})$
$=\cfrac{1}{3}(\vec{a}-2\vec{b}+2\vec{c})$
$|\overrightarrow{\text{GF}}|$ を求めると
$|\overrightarrow{\text{GF}}|^2=\cfrac{1}{3^2}(\vec{a}-2\vec{b}+2\vec{c})^2$
ここで $\overrightarrow{\text{OA}}$⊥$\overrightarrow{\text{OB}}$,$\overrightarrow{\text{OB}}$⊥$\overrightarrow{\text{OC}}$,$\overrightarrow{\text{OC}}$⊥$\overrightarrow{\text{OA}}$ より $\vec{a}\cdot\vec{b}=0$,$\vec{b}\cdot\vec{c}=0$,$\vec{c}\cdot\vec{a}=0$ が成り立つことに注意して
$=\cfrac{1}{9}(|\vec{a}|^2+4|\vec{b}|^2+4|\vec{c}|^2)$
$|\overrightarrow{\text{GF}}|^2=\cfrac{1}{9}(5+4\cdot16+4\cdot3)=9$
$|\overrightarrow{\text{GF}}|=3$
$\overrightarrow{\text{GF}}\cdot\overrightarrow{\text{GH}}$ を求める。
$\overrightarrow{\text{GH}}=\overrightarrow{\text{OH}}-\overrightarrow{\text{OG}}$
$=t\vec{c}-\cfrac{1}{3}(2\vec{a}+2\vec{b}+\vec{c})$
$\overrightarrow{\text{GF}}\cdot\overrightarrow{\text{GH}}=\bigg\{\cfrac{1}{3}(\vec{a}-2\vec{b}+2\vec{c})\bigg\}\times\bigg\{t\vec{c}-\cfrac{1}{3}(2\vec{a}+2\vec{b}+\vec{c})\bigg\}$
$\vec{a}\cdot\vec{b}=0$,$\vec{b}\cdot\vec{c}=0$,$\vec{c}\cdot\vec{a}=0$ に注意して
$=\cfrac{t}{3}\cdot2|\vec{c}|^2-\cfrac{1}{9}(2|\vec{a}|^2-4|\vec{b}|^2+2|\vec{c}|^2)$
$=\cfrac{2}{3}t\cdot3-\cfrac{1}{9}(2\cdot5-4\cdot16+2\cdot3)$
$=2t+\cfrac{16}{3}$
次に,$\overrightarrow{\text{GF}}\cdot\overrightarrow{\text{GH}}=k\overrightarrow{\text{GM}}\cdot\overrightarrow{\text{GH}}$ とおき,∠FGH=∠MGH=$\theta$ とすると,内積の公式より
$\overrightarrow{\text{GF}}\cdot\overrightarrow{\text{GH}}=k\overrightarrow{\text{GM}}\cdot\overrightarrow{\text{GH}}$
$|\overrightarrow{\text{GF}}||\overrightarrow{\text{GH}}|\cos\theta=k|\overrightarrow{\text{GM}}||\overrightarrow{\text{GH}}|\cos\theta$
$|\overrightarrow{\text{GF}}|=k|\overrightarrow{\text{GM}}|$
$3=2k$
$k=\cfrac{3}{2}$
したがって
$\overrightarrow{\text{GF}}\cdot\overrightarrow{\text{GH}}=\cfrac{3}{2}\overrightarrow{\text{GM}}\cdot\overrightarrow{\text{GH}}$
$2t+\cfrac{16}{3}=\cfrac{3}{2}\bigg(2t+\cfrac{10}{3}\bigg)$
これを解いて,$t=\cfrac{1}{3}$
SNSでシェア