【スマホで読む・わかりやすい】センター数学IIB2012本試【解説・正解・問題】
第2問
座表平面上で曲線 $y=x^3$ を $C$ とし,放物線 $y=x^2+px+q$ を $D$ とする。
(1) 曲線 $C$ 上の点 P$(a,a^3)$ における $C$ の接線の方程式は
$y=3a^{\boxed{\text{ア}}}x-\boxed{\text{ イ }}a^{\boxed{\text{ウ}}}$
である。放物線 $D$ は点 P を通り,$D$ の P における接線と,$C$ の P における接線が一致するとする。このとき,$p$ と $q$ を $a$ を用いて表すと
$\begin{cases}p=3a^{\boxed{\text{ エ }}}-\boxed{\text{ オ }}a\\q=\boxed{\text{ カキ }}a^3+a^{\boxed{\text{ ク }}}\end{cases}$…①
となる。
以下,$p$,$q$ は①を満たすとする。
(2) 放物線 $D$ が $y$ 軸上の与えられた点Q$(0,b)$ を通るとき
$b=\boxed{\text{ ケコ }}a^3+a^{\boxed{\text{サ}}}$…②
が成り立つ。与えられた $b$ に対して,②を満たす $a$ の値の個数を調べよう。
そのために,関数
$f(x)=\boxed{\text{ ケコ }}x^3+x^{\boxed{\text{サ}}}$
の増減を調べる。関数 $f(x)$ は,$x=\boxed{\text{ シ }}$ で極小値 $\boxed{\text{ ス }}$ をとり,$ x=\cfrac{\boxed{\text{ セ }}}{\boxed{\text{ ソ }}}$ で極大値 $\cfrac{\boxed{\text{ タ }}}{\boxed{\text{ チツ }}}$ をとる。
関数 $y=f(x)$ のグラフをかくことにより,$\boxed{\text{ ス }} < b < \cfrac{\boxed{\text{ タ }}}{\boxed{\text{ チツ }}}$ のとき,② を満たす $a$ の値の個数は $\boxed{\text{ テ }}$ であることがわかる。
(3) 放物線 $D$ の頂点が $x$ 軸上にあるのは,$a=\boxed{\text{ ト }}$,$\cfrac{\boxed{\text{ ナ }}}{\boxed{\text{ ニ }}}$ の二つの場合である。$a=\boxed{\text{ ト }}$ のときの放物線を $D_1$,$a=\cfrac{\boxed{\text{ ナ }}}{\boxed{\text{ ニ }}}$ のときの放物線を $D_2$ とする。$D_1$,$D_2$ と $x$ 軸で囲まれた図形の面積は $\cfrac{2^{\boxed{\text{ヌ}}}}{3^{\boxed{\text{ネノ}}}}$ である。
正解と解説
ア,イ,ウ 2,2,3
エ,オ 2,2
カキ,ク -2,2
ケコ,サ -2,2
シ 0
ス 0
$\cfrac{\text{セ}}{\text{ソ}}$ $\cfrac{1}{3}$ $\cfrac{\text{タ}}{\text{チツ}}$
$\cfrac{1}{27}$
テ 3
ト 0
$\cfrac{\text{ナ}}{\text{ニ}}$ $\cfrac{4}{9}$
ヌ,ネノ 4,10
(1)
式を微分して接線の傾きを求め,$x$ 座標が $a$ のときの接線の方程式を作るとよい。
$C : y=x^3$
$y’=3x^2$
$x=a$ のとき接線の傾きは $3a^2$ となるので接線の方程式は
$y-a^3=3a^2(x-a)$
$y=3a^2x-2a^3$
同様に $D$ について接線の方程式を求めると
$D:y=x^2+px+q$
$y’=2x+p$
$y-a^2-pa-q=(2a+p)(x-a)$
$y=(2a+p)x-(2a+p)a+a^2+pa+q$
$y=(2a+p)x-a^2+q$
2つの接線は一致することから,おたがいの係数を比べると
$\begin{cases}3a^2=2a+p\\-2a^3=-a^2+q\end{cases}$
これより
$p=3a^2-2a$
$q=-2a^3+a^2$
(2)
$D$ に点 Q の座標を代入すると
$b=q$
上で求めた $q$ の式を代入して
$b=-2a^3+a^2$
次に関数 $f(x)$ の増減を調べるために微分して増減表をつくる。
$f(x)=-2x^3+x^2$
$f'(x)=-6x^2+2x$
$-6x^2+2x=0$ とおくと
$-6x(x-\cfrac{1}{3})=0$
$x=0,\space\cfrac{1}{3}$
| $x$ | $\cdots$ | $0$ | $\cdots$ | $\cfrac{1}{3}$ | $\cdots$ |
| $f'(x)$ | $-$ | $0$ | $+$ | $0$ | $-$ |
| $f(x)$ | $\searrow$ | $0$ | $\nearrow$ | $\cfrac{1}{27}$ | $\searrow$ |
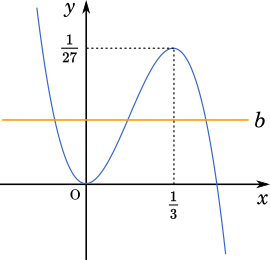
関数 $f(x)$ は,$x=0$ で極小値 $0$ をとり,$x=\cfrac{1}{3}$ で極大値 $\cfrac{1}{27}$ をとる。
グラフを書いてみると,$0 < b < \cfrac{1}{27}$ のとき,②を満たす $a$ の値の個数は 3 である。
(3)
$D$ を平方完成して頂点の座標を求める。
$y=x^2+px+q$
$=\bigg(x+\cfrac{p}{2}\bigg)^2-\cfrac{p^2}{4}+q$
頂点は $\bigg(-\cfrac{p}{2},\space-\cfrac{p^2}{4}+q\bigg)$
頂点が $x$ 軸上にあるとき $y$ 座標が $0$ になるので
$-\cfrac{p^2}{4}+q=0$
上で求めた $p$,$q$ の式を代入すると
$-\cfrac{(3a^2-2a)^2}{4}-2a^3+a^2=0$
$(3a^2-2a)^2+8a^3-4a^2=0$
$9a^4-12a^3+4a^2+8a^3-4a^2=0$
$9a^4-4a^3=0$
$a^3(9a-4)=0$
$a=0,\space\cfrac{4}{9}$
$D_1$,$D_2$ と $x$ 軸で囲まれた図形の面積を求める。
$D_1$ の頂点の $x$ 座標を考えると,$a=0$ のとき $p=0$ となり $-\cfrac{p}{2}=0$ である。つまり,頂点は原点である。
また $D_2$ の頂点の $x$ 座標を考えると,$a=\cfrac{4}{9}$ のとき $p$ は
$p=3\times\bigg(\cfrac{4}{9}\bigg)^2-2\times\bigg(\cfrac{4}{9}\bigg)=-\cfrac{8}{27}$
$-\cfrac{p}{2}=\cfrac{4}{27}$
となる。
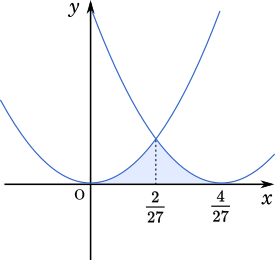
$D_1$ と $D_2$ は同じ形の放物線を平行移動させたものであることに注意すると,$D_1$ と $D_2$ はちょうど真ん中の $x=\cfrac{2}{27}$ で交わる。そこで図形の面積を 2 つに分けて計算したものを 2 倍すればよいことが分かる。
$\displaystyle\cfrac{S}{2}=\int_0^{\small{\cfrac{2}{27}}} x^2\space dx$
$=\bigg[\cfrac{x^3}{3}\bigg]_0^{\small{\cfrac{2}{27}}}$
$=\cfrac{1}{3}\bigg(\cfrac{2}{27}\bigg)^3$
$=\cfrac{1}{3}\bigg(\cfrac{2}{3^3}\bigg)^3$
$=\cfrac{2^3}{3^{10}}$
$S=\cfrac{2^4}{3^{10}}$
SNSでシェア