【スマホで読む・わかりやすい】センター数学IIB2012本試【解説・正解・問題】

第1問

〔1〕　$a > 0$，$a\not = 1$ として，不等式
$2\log_a(8-x) > \log_a (x-2)\cdots$①
を満たす $x$ の値の範囲を求めよう。
真数は正であるから，$\boxed{\text{ ア }} < x < \boxed{\text{ イ }}$ が成り立つ。ただし，対数 $\log_a b$ に対し，$a$ を底といい，$b$ を真数という。
底 $a$ が $a < 1$ を満たすとき，不等式①は
$x^2-\boxed{\text{ ウエ }}x+\boxed{\text{ オカ }}\space\boxed{\text{ キ }}\space 0\cdots$②
となる。ただし，$\boxed{\text{ キ }}$ については，当てはまるものを，次の⓪～②のうちから一つ選べ。

⓪ $ < $　① $=$　② $ > $

したがって，真数が正であることと②から，$a < 1$ のとき，不等式①を満たす $x$ のとり得る値の範囲は $\boxed{\text{ ク }} < x < \boxed{\text{ ケ }}$ である。
同様にして，$a > 1$ のときには，不等式①を満たす $x$ のとり得る値の範囲は $\boxed{\text{ コ }} < x < \boxed{\text{ サ }}$ であることがわかる。

〔2〕 $0\leqq \alpha \leqq \pi$ として
$\sin \alpha = \cos 2\beta$
を満たす $\beta$ について考えよう。ただし，$0\leqq \beta\leqq\pi$ とする。
たとえば，$\alpha=\cfrac{\pi}{6}$ のとき，$\beta$ のとり得る値は $\cfrac{\pi}{\boxed{\text{ シ }}}$ と $\cfrac{\boxed{\text{ ス }}}{\boxed{\text{ シ }}}\pi$ の二つである。
このように，$\alpha$ の各値に対して，$\beta$ のとり得る値は二つある。そのうちの小さい方を $\beta_1$，大きい方を $\beta_2$ とし
$y=\sin\bigg(\alpha+\cfrac{\beta_1}{2}+\cfrac{\beta_2}{3}\bigg)$
が最大となる $\alpha$ の値とそのときの $y$ の値を求めよう。
$\beta_1$，$\beta_2$ を $\alpha$ を用いて表すと，$0\leqq\alpha\leqq\cfrac{\pi}{2}$ のときは
$\beta_1=\cfrac{\pi}{\boxed{\text{ セ }}}-\cfrac{\alpha}{\boxed{\text{ ソ }}}$，$\beta_2=\cfrac{\boxed{\text{ タ }}}{\boxed{\text{ セ }}}\pi+\cfrac{\alpha}{\boxed{\text{ ソ }}}$
となり，$\cfrac{\pi}{2}\leqq\alpha\leqq\pi$ のときは
$\beta_1=-\cfrac{\pi}{\boxed{\text{ チ }}}+\cfrac{\alpha}{\boxed{\text{ ツ }}}$，$\beta_2=\cfrac{\boxed{\text{ テ }}}{\boxed{\text{ チ }}}\pi-\cfrac{\alpha}{\boxed{\text{ ツ }}}$
となる。
したがって，$\alpha+\cfrac{\beta_1}{2}+\cfrac{\beta_2}{3}$ のとり得る値の範囲は
$\cfrac{\boxed{\text{ ト }}}{\boxed{\text{ ナ }}}\pi\leqq\alpha+\cfrac{\beta_1}{2}+\cfrac{\beta_2}{3}\leqq\cfrac{\boxed{\text{ ニヌ }}}{\boxed{\text{ ネ }}}\pi$
である。よって，$y$ が最大となる $\alpha$ の値は $\cfrac{\boxed{\text{ ノ }}}{\boxed{\text{ ハヒ }}}\pi$ であり，そのときの $y$ の値は $\boxed{\text{ フ }}$ であることがわかる。$\boxed{\text{ フ }}$ に当てはまるものを，次の⓪～③のうちから一つ選べ。

⓪ $\cfrac{1}{2}$　① $1$
② $\cfrac{\sqrt{2}}{2}$ 　③ $\cfrac{\sqrt{3}}{2}$

正解と解説

ア 2

イ 8

ウエ,オカ 17,66

キ 0

ク 6

ケ 8

コ 2

サ 6

シ 6

ス 5

セ,ソ 4,2
タ 3

チ,ツ 4,2

テ 5

$\cfrac{\text{ト}}{\text{ナ}}$ $\cfrac{3}{8}$

$\cfrac{ニヌ}{ネ}$ $\cfrac{11}{8}$

$\cfrac{ノ}{ハヒ}$ $\cfrac{3}{22}$

フ 1

$a > 0$，$a\not =1$ のときを考えると
$2\log_a (8-x) > \log_a (x-2)\cdots$①
真数条件（真数は正の値）より
$8-x > 0$
$x < 8$ また $x-2 > 0$
$x > 2$
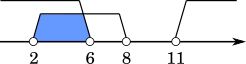
だから，$2 < x < 8$
次に $a < 1$ のときを考えると，①を変形して $\log_a (8-x)^2 > \log_a (x-2)$
底が 1 より小さい数のとき真数どうしを比べると不等号の向きが逆になることに注意して
$(8-x)^2 < x-2$
$64-16x+x^2 < x-2$
$x^2-17x+66 < 0\cdots$②
$(x-11)(x-6) < 0$
$6 < x < 11$
これと $2 < x < 8$ を重ねると
$6 < x < 8$ 同様にして，$a > 1$ のときには
$(x-11)(x-6) > 0$
$x < 6$，$11 < x$
これと $2 < x < 8$ を重ねると
$2 < x < 6$

〔2〕

$\alpha=\cfrac{\pi}{6}$ のとき
$\sin\cfrac{\pi}{6}=\cos 2\beta$
$\cos 2\beta=\cfrac{1}{2}$
$2\beta=\cfrac{\pi}{3},\space\cfrac{5}{3}\pi$
$\beta=\cfrac{\pi}{6},\space\cfrac{5}{6}\pi$
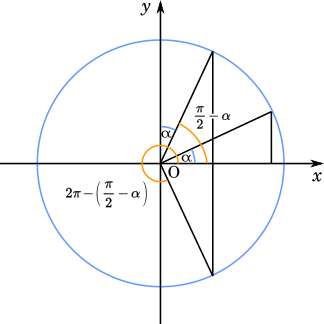
次に $0\leqq\alpha < \cfrac{\pi}{2}$ のとき
$2\beta_1=\cfrac{\pi}{2}-\alpha$
$\beta_1=\cfrac{\pi}{4}-\cfrac{\alpha}{2}$
$2\beta_2=2\pi-\bigg(\cfrac{\pi}{2}-\alpha\bigg)$
$\beta_2=\cfrac{3}{4}\pi+\cfrac{\alpha}{2}$

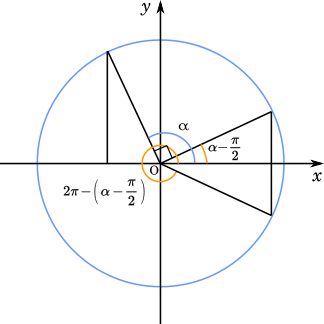
$\cfrac{\pi}{2}\leqq\alpha\leqq\pi$ のとき
$2\beta_1=\alpha-\cfrac{\pi}{2}$
$\beta_1=-\cfrac{\pi}{4}+\cfrac{\alpha}{2}$
$2\beta_2=2\pi-\bigg(\alpha-\cfrac{\pi}{2}\bigg)$
$\beta_2=\cfrac{5}{4}\pi-\cfrac{\alpha}{2}$

$\alpha+\cfrac{\beta_1}{2}+\cfrac{\beta_2}{3}$ のとり得る範囲を求める。

(i) $0\leqq\alpha <\cfrac{\pi}{2}$ のとき
$\alpha+\cfrac{\beta_1}{2}+\cfrac{\beta_2}{3}=\alpha+\cfrac{\pi}{8}-\cfrac{\alpha}{4}+\cfrac{3}{12}\pi+\cfrac{\alpha}{6}$
$=\cfrac{11}{12}\alpha+\cfrac{3}{8}\pi$
ここで，$0\leqq\alpha <\cfrac{\pi}{2}$ を変形して
$0\leqq\cfrac{11}{12}\alpha < \cfrac{11}{24}\pi$
$\cfrac{3}{8}\pi\leqq\cfrac{11}{12}\alpha+\cfrac{3}{8}\pi < \cfrac{5}{6}\pi$

(ii) $\cfrac{\pi}{2}\leqq\alpha\leqq\pi$ のとき
$\alpha+\cfrac{\beta_1}{2}+\cfrac{\beta_2}{3}=\alpha-\cfrac{\pi}{8}+\cfrac{\alpha}{4}+\cfrac{5}{12}\pi-\cfrac{\alpha}{6}$
$=\cfrac{13}{12}\alpha+\cfrac{7}{24}\pi$
$\cfrac{\pi}{2}\leqq\alpha\leqq\pi$ を変形して
$\cfrac{13}{24}\pi\leqq\cfrac{13}{12}\alpha\leqq\cfrac{13}{12}\pi$
$\cfrac{5}{6}\pi\leqq\cfrac{13}{12}\alpha+\cfrac{7}{24}\pi\leqq\cfrac{11}{8}\pi$
(i),(ii)で求めた範囲を重ねると
$\cfrac{5}{6}\pi\leqq\alpha+\cfrac{\beta_1}{2}+\cfrac{\beta_2}{3}\leqq\cfrac{11}{8}\pi$
したがって，$\sin\bigg(\alpha+\cfrac{\beta_1}{2}+\cfrac{\beta_2}{3}\bigg)$ は $\alpha+\cfrac{\beta_1}{2}+\cfrac{\beta_2}{3}=\cfrac{\pi}{2}$ で最大値 $y=1$ をとる。

さらに $\alpha$ を求める。
(i) で求めた式を用いて
$\alpha+\cfrac{\beta_1}{2}+\cfrac{\beta_2}{3}=\cfrac{11}{12}\alpha+\cfrac{3}{8}\pi=\cfrac{\pi}{2}$
$\cfrac{11}{12}\alpha=\cfrac{\pi}{8}$
$\alpha=\cfrac{3}{22}\pi$