【スマホで読む・わかりやすい】センター数学IA2020追試【解説・正解・問題】

第５問

正解と解説

ア 4　イ 6　ウ,エ 2, 6
オカ,キク 19, 35
ケコ,サ 19, 7
シス,セ 19,5
ソ,タ,チツ 5, 6, 12

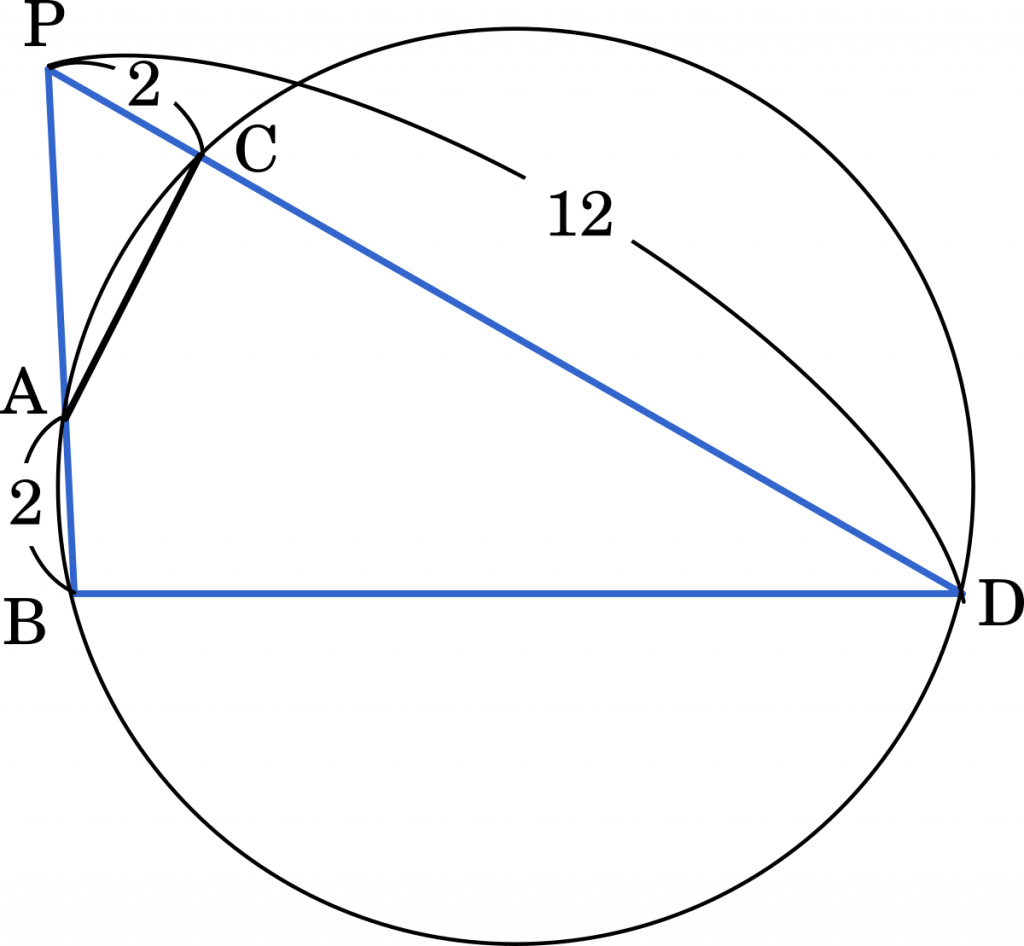
方べきの定理より

$\text{PA}\cdot\text{PB}=\text{PC}\cdot\text{PD}$

$\text{PB}=\text{PA}+2$ より

$\text{PA}(\text{PA}+2)=2\cdot12$
$\text{PA}^2+2\text{PA}-24=0$
$(\text{PA}+6)(\text{PA}-4)=0$
$\text{PA}=4,-6$

$\text{PA}>0$ より

$\text{PA}=4$

・・・ア

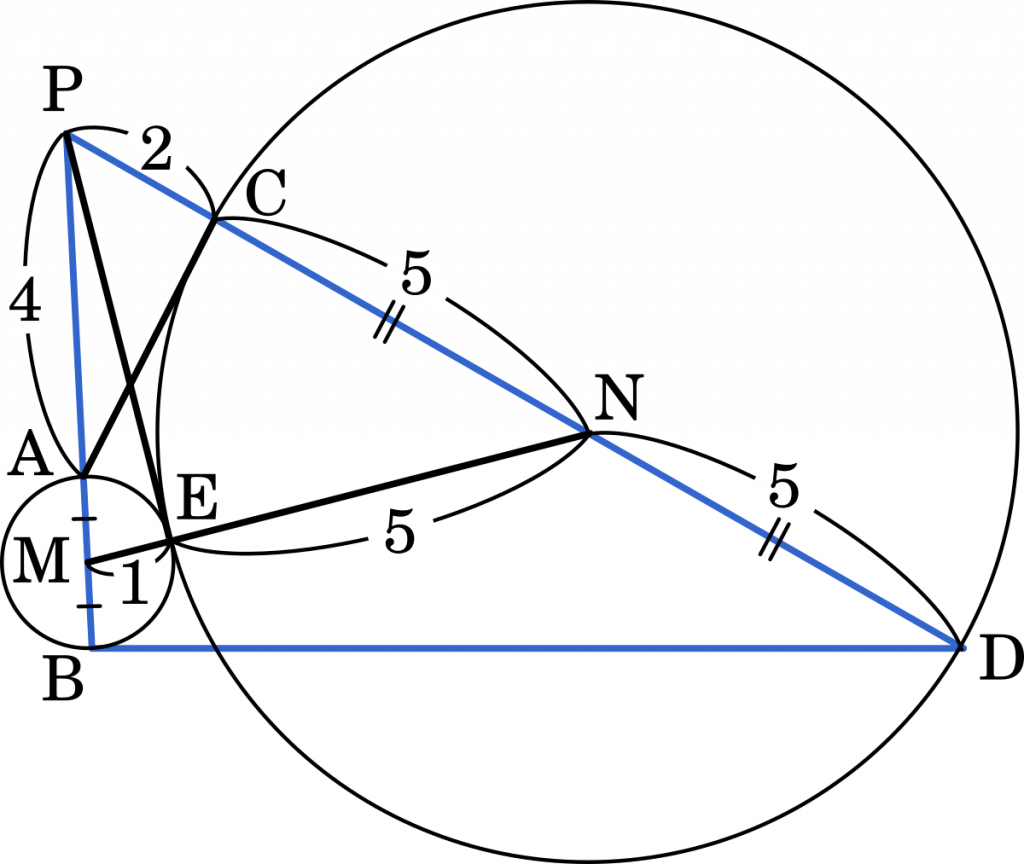
図より　$\text{MN}=6$

・・・イ

余弦定理を用いて

$6^2=5^2+7^2-2\cdot5\cdot7\cos\angle\text{MPN}$
$36=25+49-70\cos\angle\text{MPN}$
$70\cos\angle\text{MPN}=38$
$\cos\angle\text{MPN}=\cfrac{19}{35}$

・・・オカキク

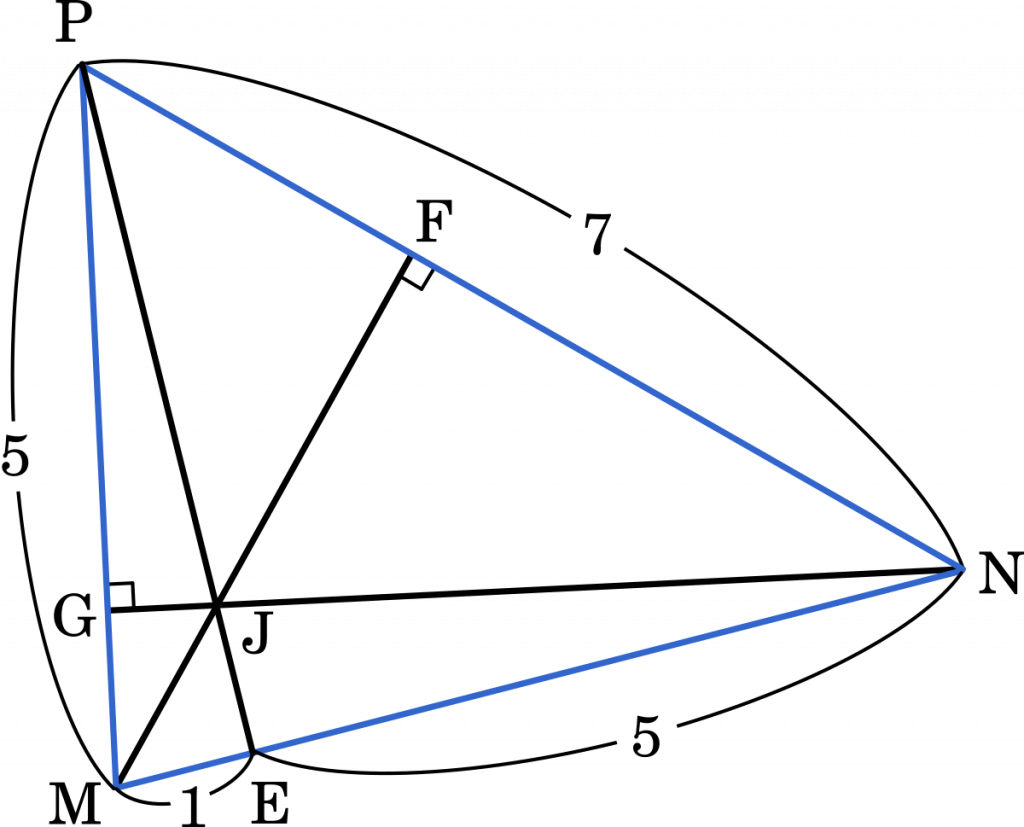
三平方の定理を用いて

$\text{FN}^2+\text{FM}^2=6^2$
$(7-\text{PF})^2+\text{FM}^2=36$
$\text{FM}^2=36-(7-\text{PF})^2$

また

$\text{PF}^2+\text{FM}^2=5^2$
$\text{FM}^2=25-\text{PF}^2$

よって

$36-(7-\text{PF})^2=25-\text{PF}^2$
$36-(49-14\text{PF}+\text{PF}^2)=25-\text{PF}^2$
$14\text{PF}=38$
$\text{PF}=\cfrac{38}{14}=\cfrac{19}{7}$

・・・ケコサ

同様にして

$\text{GM}^2+\text{GN}^2=6^2$
$(5-\text{PG})^2+\text{GN}^2=36$
$\text{GN}^2=36-(5-\text{PG})^2$

また

$\text{PG}^2+\text{GN}^2=7^2$
$\text{GN}^2=49-\text{PG}^2$

よって

$36-(5-\text{PG})^2=49-\text{PG}^2$
$36-(25-10\text{PG}+\text{PG}^2)=49-\text{PG}^2$
$10\text{PG}=38$
$\text{PG}=\cfrac{38}{10}=\cfrac{19}{5}$

・・・シスセ

また，メネラウスの定理を用いて

$\cfrac{\text{PG}}{\text{GM}}\times\cfrac{6}{5}\times\cfrac{\text{EJ}}{\text{JP}}=1$
$\cfrac{\cfrac{19}{5}}{5-\cfrac{19}{5}}\times\cfrac{6}{5}\times\cfrac{\text{EJ}}{\text{JP}}=1$
$\cfrac{\enspace\cfrac{19}{5}\enspace}{\cfrac{6}{5}}\times\cfrac{6}{5}\times\cfrac{\text{EJ}}{\text{JP}}=1$
$\cfrac{\enspace\cfrac{19}{5}\times5\enspace}{\cfrac{6}{5}\times5}\times\cfrac{6}{5}\times\cfrac{\text{EJ}}{\text{JP}}=1$
$\cfrac{19}{6}\times\cfrac{6}{5}\times\cfrac{\text{EJ}}{\text{JP}}=1$
$\cfrac{19}{5}\times\cfrac{\text{EJ}}{\text{JP}}=1$
$\cfrac{\text{EJ}}{\text{JP}}=\cfrac{5}{19}$

よって

EJ : JP = 5 : 19

が成り立つ。

PE = $2\sqrt{6}$ より

JE = $2\sqrt{6}\times\cfrac{5}{24}$
$=\cfrac{5\sqrt{6}}{12}$

・・・ソタチツ

問題文

　△PBD の辺 PB 上に 2 点 P，B のいずれとも異なる点 A をとり，辺 PD 上に 2 点 P，D のいずれとも異なる点 C をとる。 4 点 A，B，C，D が同一円周上にあり，AB ＝ 2，PC ＝ 2，PD ＝ 12 のとき，PA ＝ $\boxed{\text{ ア }}$ である。
　点 M を線分 AB の中点とし，点 N を線分 CD の中点とする。線分 AB を直径とする円と線分 CD を直径とする円が点 E で接していて，3 点 M，E，N が一直線上にこの順に並んでいるとする。このとき
MN ＝ $\boxed{\text{ イ }}$，PE ＝ $\boxed{\text{ ウ }}\sqrt{\boxed{\text{ エ }}}$
である。また
$\cos\angle\text{MPN}=\cfrac{\boxed{\text{ オカ }}}{\boxed{\text{ キク }}}$
である。
線分 PN 上に点 F を直線 MF と直線 PN が垂直に交わるようにとり，線分 PM 上に点 G を直線 NG と直線 PM が垂直に交わるようにとる。このとき
PF ＝ $\cfrac{\boxed{\text{ ケコ }}}{\boxed{\text{ サ }}}$，PG ＝ $\cfrac{\boxed{\text{ シス }}}{\boxed{\text{ セ }}}$
である。さらに，線分 MF と線分 NG の交点を J とする。このとき
JE ＝ $\cfrac{\boxed{\text{ ソ }}\sqrt{\boxed{\text{ タ }}}}{\boxed{\text{ チツ }}}$
である。