【スマホで読む・わかりやすい】センター数学IA2020追試【解説・正解・問題】
第2問
正解と解説
ア 4 イ 2 ウ,エ 9, 5
オカ,キ,ク 51, 2, 8
ケコ 36 サ 3 シ 1
ス,セ 1, 3 ソ 2
タ,チ 6, 4 ツ 2
〔1〕

余弦定理を用いることを考え,いったん $\cos$ の値を求めるとよい。
$\sin\angle\text{PAB}=\cfrac{2\sqrt{2}}{2}$ だから
$\sin^2\angle\text{PAB}=\cfrac{8}{9}$
公式 $\sin^2x+\cos^2x=1$ より
$\cfrac{8}{9}+\cos^2\angle\text{PAB}=1$
$\cos^2\angle\text{PAB}=\cfrac{1}{9}$
$\cos\angle\text{PAB}=\pm\cfrac{1}{3}$
余弦定理を用いて
$(2\sqrt{17})^2=\text{AB}^2+6^2-2\cdot\text{AB}\cdot6\cdot\cos\angle\text{PAB}$
$68=\text{AB}^2+36-12\text{AB}\cdot\cos\angle\text{PAB}$
$\text{AB}^2-12\text{AB}\cdot\cos\angle\text{PAB}-32=0$
(i) $\cos\angle\text{PAB}=\cfrac{1}{3}$ のとき
$\text{AB}^2-12\text{AB}\cdot\cfrac{1}{3}-32=0$
$\text{AB}^2-4\text{AB}-32=0$
$(\text{AB}-8)(\text{AB}+4)=0$
$\text{AB}=-4,8$
(ii) $\cos\angle\text{PAB}=-\cfrac{1}{3}$ のとき
$\text{AB}^2+4\text{AB}-32=0$
$(\text{AB}+8)(\text{AB}-4)=0$
$\text{AB}=4,-8$
問題文より,AB < AP に注意すると,AB は 0 以上 6 未満の値である。
したがって
AB = 4
・・・ア
よって,$\cos\angle\text{PAB}=-\cfrac{1}{3}$ となる。
$\cos$ は 90° 以上 180° 以下で負の値をとることに注意すると,
$\angle\text{PAB}$ は鈍角である。
・・・イ

余弦定理を用いて
$(3\sqrt{17})^2=\text{AC}^2+6^2-2\text{AC}\cdot6\cdot\cos\angle\text{PAC}$
$153=\text{AC}^2+36-12\text{AC}\Big(-\cfrac{1}{3}\Big)$
$\text{AC}^2+4\text{AC}-117=0$
$(\text{AC}-9)(\text{AC}+13)=0$
$\text{AC}=9,-13$
AC > 0 より
AC = 9
・・・ウ
したがって
BC = $9-4=5$
・・・エ
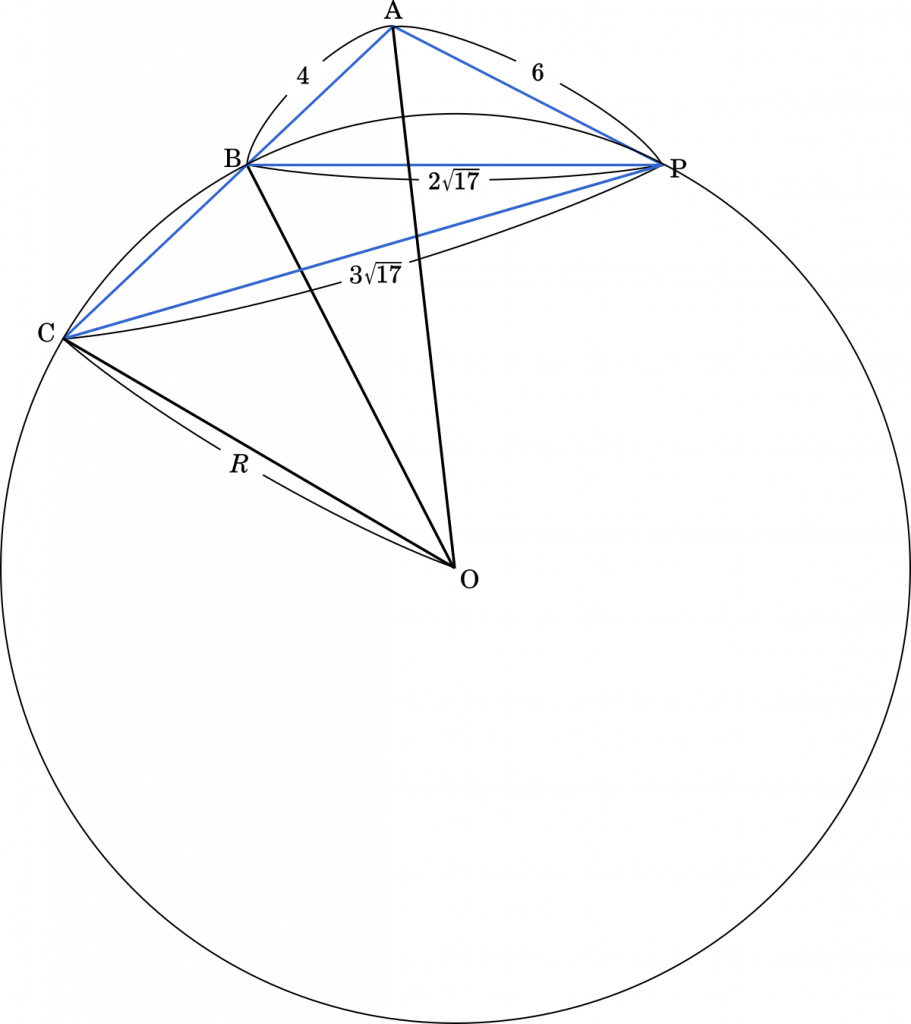
△PBC の外接円の半径 $R$ を求める。
△PAC において,正弦定理より
$\cfrac{3\sqrt{17}}{\sin\angle\text{PAC}}=\cfrac{6}{\sin\angle\text{PCA}}$
$\sin\angle\text{PCA}=\cfrac{6\sin\angle\text{PAC}}{3\sqrt{17}}$
$=\cfrac{6\cdot\cfrac{2\sqrt{2}}{3}}{3\sqrt{17}}=\cfrac{4\sqrt{2}}{3\sqrt{17}}$
また,△PBC において,正弦定理より
$2R=\cfrac{2\sqrt{17}}{\sin\angle\text{PCB}}$
$\sin\angle\text{PCB}=\sin\angle\text{PCA}$ だから
$2R=\cfrac{\enspace2\sqrt{17}\enspace}{\cfrac{4\sqrt{2}}{3\sqrt{17}}}$
$=\cfrac{\enspace2\sqrt{17}\times3\sqrt{17}\enspace}{\cfrac{4\sqrt{2}}{3\sqrt{17}}\times3\sqrt{17}}$
$=\cfrac{102}{4\sqrt{2}}=\cfrac{51}{2\sqrt{2}}$
$=\cfrac{51\sqrt{2}}{4}$
したがって
$R=\cfrac{51\sqrt{2}}{8}$
・・・オカキク
さらに,$\angle\text{OAB}=\angle\text{OAC}$ であることを利用して,△AOB と △AOC において余弦定理を用いるとよい。
△AOB において
$R^2=\text{AO}^2+4^2-2\text{AO}\cdot4\cos\angle\text{OAB}$
$R^2=\text{AO}^2+16-8\text{AO}\cos\angle\text{OAB}$
$8\text{AO}\cos\angle\text{OAB}=\text{AO}^2-R^2+16$
$\cos\angle\text{OAB}=\cfrac{\text{AO}^2-R^2+16}{8\text{AO}}$
また,△AOC において
$R^2=\text{AO}^2+9^2-2\text{AO}\cdot9\cos\angle\text{OAC}$
$\cos\angle\text{OAC}=\cos\angle\text{OAB}$ だから
$R^2=\text{AO}^2+81-18\text{AO}\cdot\cfrac{\text{AO}^2-R^2+16}{8\text{AO}}$
$R^2=\text{AO}^2+81-\cfrac{9}{4}(\text{AO}^2-R^2+16)$
$4R^2=4\text{AO}^2+324-9\text{AO}^2+9R^2-144$
$5\text{AO}^2-5R^2=180$
$\text{AO}^2-R^2=36$
・・・ケコ
〔2〕(1)
47 都道府県を四分位範囲に分けると,このようになる。
$\begin{matrix}\underbrace{\circ\circ\circ\cdots\cdots\cdots\circ\circ}_\text{23個}&|&\underbrace{\circ}_{\text{中央値}}&|&\underbrace{\circ\circ\circ\cdots\cdots\cdots\circ\circ}_\text{23個}\\\underbrace{\circ\cdots\circ}_\text{11個}|\underbrace{\circ}_\text{Q1}|\underbrace{\circ\cdots\circ}_\text{11個} &&&&\underbrace{\circ\cdots\circ}_\text{11個}|\underbrace{\circ}_\text{Q3}|\underbrace{\circ\cdots\circ}_\text{11個}\end{matrix}$
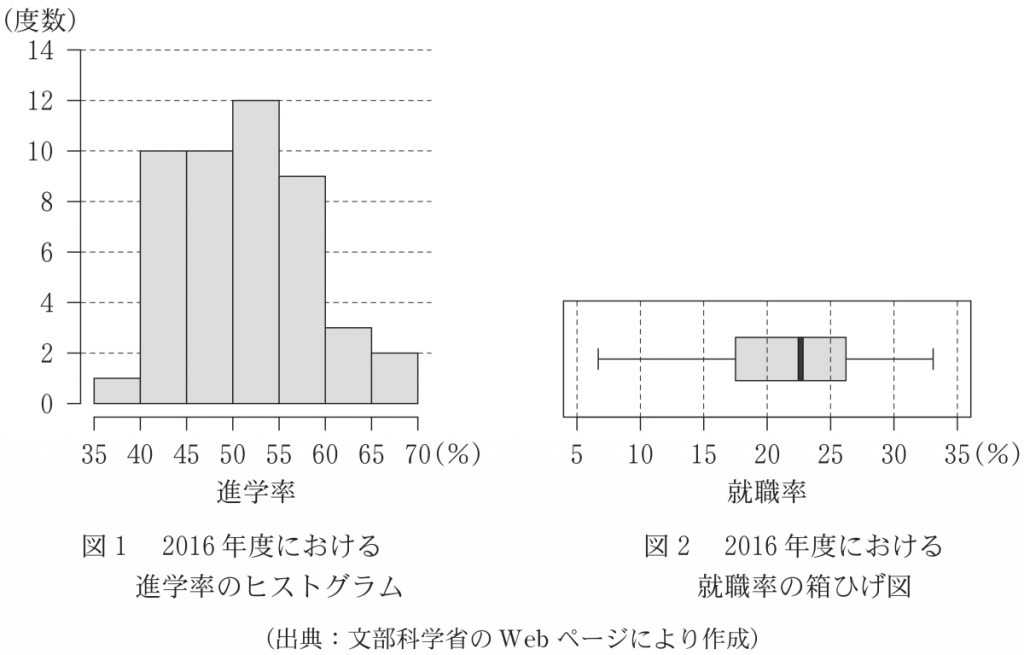
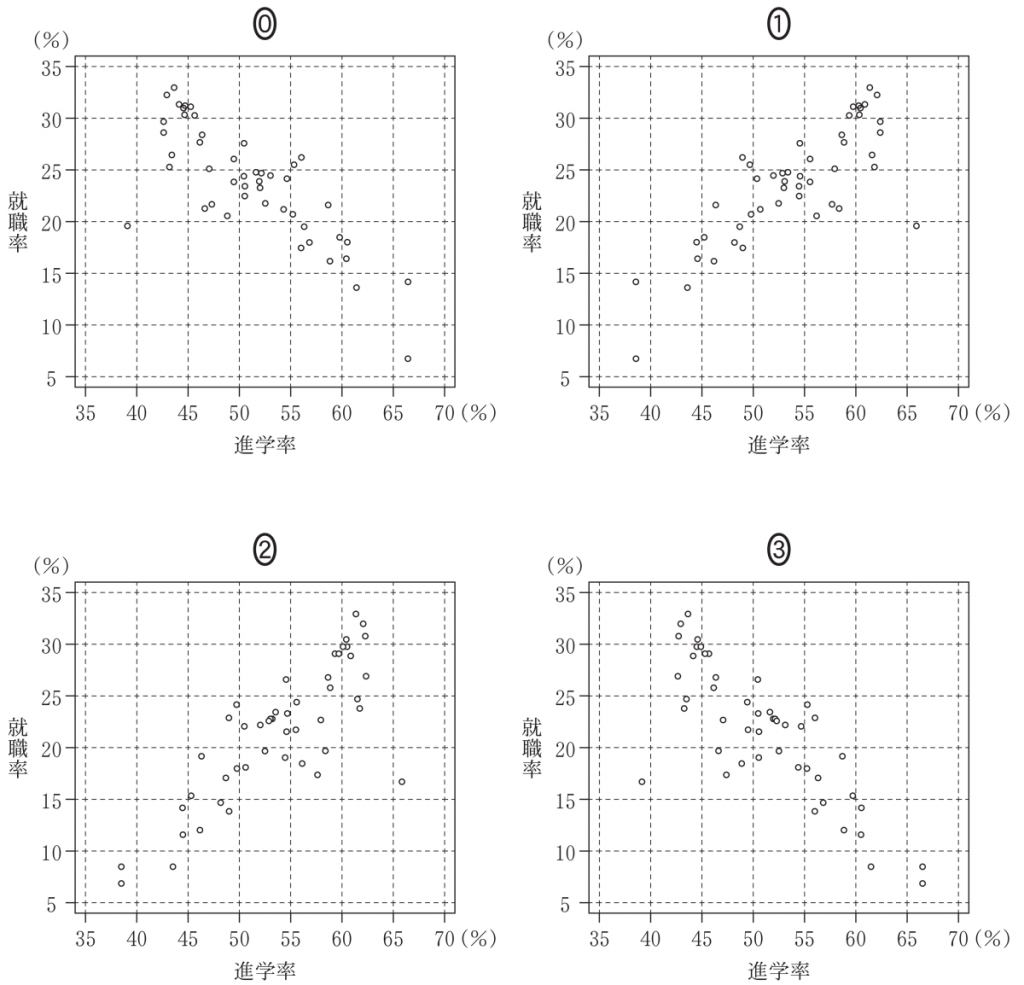
⓪ 第1四分位数に着目する。第1四分位数は下から 12 番目のデータであり,箱ひげ図を見ると 15 から 20 パーセントの間にある。しかし,散布図の就職率において下から 12 番目のデータは 20 パーセント以上にあり,不適。
①,② ヒストグラムより,進学率が 35 から 40 パーセントの間にあるデータは 1 個であるが,散布図では 2 個あるため,不適。
よって,③が正しい。
・・・サ
〔2〕(2)
⓪ 例えば,1998年度は左側の方が長い。よって,不適。
② 例えば,2008年度は直前の時点より増加している。よって,不適。
③ 例えば,1978年度は進学率の方が大きい。よって,不適。
④ 例えば,1973年度の就職率の最小値はおよそ 35 パーセントで,最大値はおよそ 65 パーセントだから,2 倍以上であるとは言えない。よって,不適。
したがって,①が正しい。
・・・シ
〔2〕(3)
就職率を下から数えていくと,34.8パーセントのデータは 24 番目にあり,これは中央値のことである。
・・・ス
また,進学率の中央値は 30 から 35 パーセントの間にある。よって,③が当てはまる。
・・・セ
〔2〕(4)
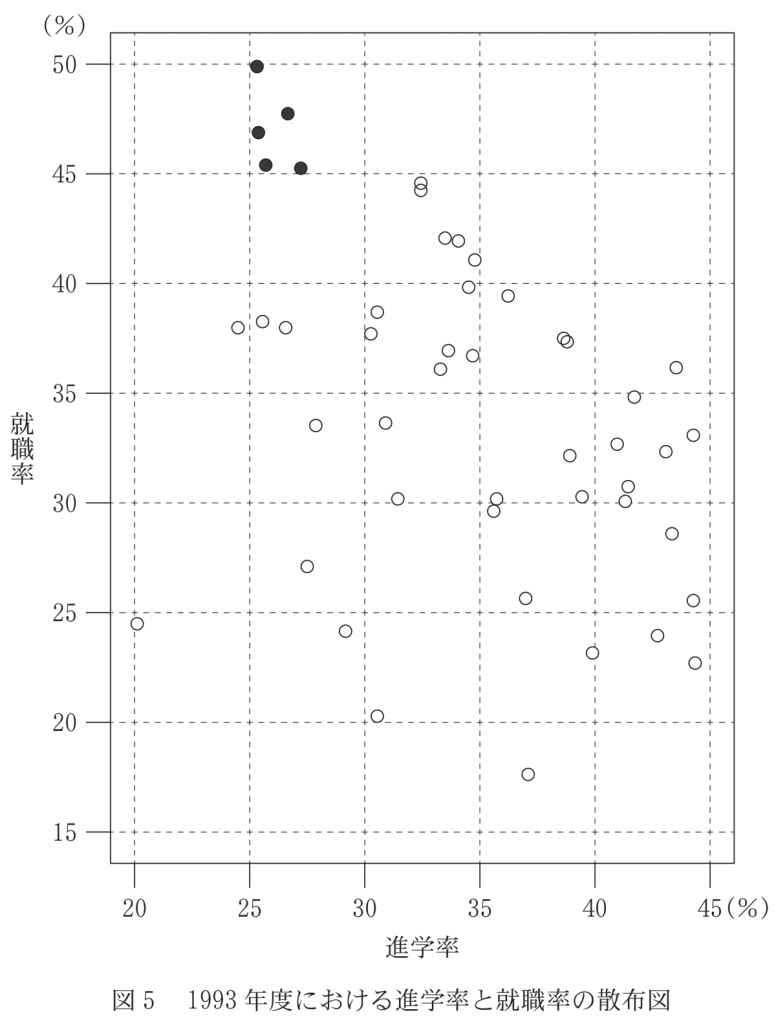
黒丸はの点はグラフの左上にあり,これらを取り除くと,負の相関が弱くなると考えられる。よって②が正しい。
・・・シ
〔2〕(5)
相関係数を求める公式 $r=\cfrac{s_{xy}}{s_x s_y}$ ($s_{xy}$ : $x$ と $y$ の共分散,$s_x$:$x$ の標準偏差,$s_y$:$y$ の標準偏差)を用いると
$-0.41=\cfrac{-20}{s_x\times7.6}$
$s_x=6.41\cdots$ だから
$s_x=6.4$
・・・タチ
さらに,問題文の式
$s^2=\cfrac{{u_1}^2+{u_2}^2+\cdots+{u_n}^2}{n}-(\bar{u})^2$
において
$\cfrac{{u_1}^2+{u_2}^2+\cdots+{u_n}^2}{n}$
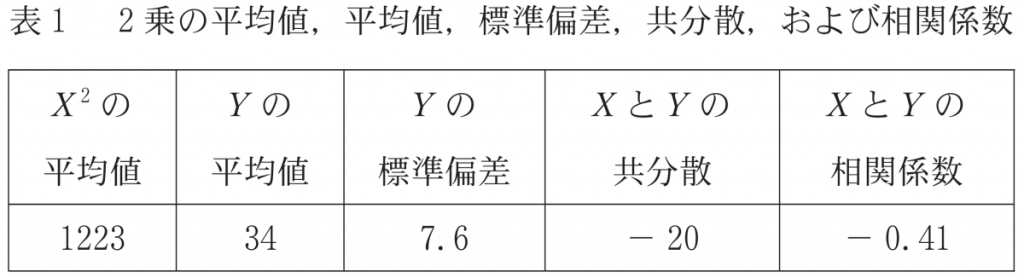
は,データの2乗の平均値を表していることが分かる。よって,表1より,値をそれぞれ代入すると
$6.4^2=1223-(\bar{x})^2$
$(\bar{x})^2=1223-40.96$
$=1182.04$
したがって,②が当てはまる。
・・・ツ
問題文
〔1〕 △ABP において,AP = 6,BP = $2\sqrt{17}$,$\sin\angle\text{PAB}=\cfrac{2\sqrt{2}}{3}$,AB < AP とする。
次の $\boxed{\text{ イ }}$ に当てはまるものを,下の⓪~②のうちから一つ選べ。 AB = $\boxed{\text{ ア }}$ であり,∠PAB は $\boxed{\text{ イ }}$ である。
⓪ 鋭角 ① 直角 ② 鈍角
直線 AB 上に点 C を,3 点 A,B,C がこの順に並び,かつ CP = $3\sqrt{17}$ となるようにとる。このとき
AC = $\boxed{\text{ ウ }}$,BC = $\boxed{\text{ エ }}$
である。したがって,△PCB の外接円の半径 $R$ は
$R=\cfrac{\boxed{\text{ オカ }}\sqrt{\boxed{\text{ キ }}}}{\boxed{\text{ ク }}}$
である。この外接円の中心を O とすると
$\text{AO}^2-R^2=\boxed{\text{ ケコ }}$
である。
〔2〕 高等学校(中等教育学校を含む)の卒業生のうち,大学または短期大学に進学した者の割合(以下,進学率)と,就職した者の割合(以下,就職率)が 47 の都道府県別に公表されている。
(1) 図 1 は 2016 年度における都道府県別の進学率のヒストグラムであり,図 2 は 2016 年度における都道府県別の就職率の箱ひげ図である。なお,ヒストグラムの各階級の区間は,左側の数値を含み,右側の数値を含まない。
次の $\boxed{\text{ サ }}$ に当てはまるものを,下の⓪~③のうちから一つ選べ。
2016 年度における都道府県別の進学率(横軸)と就職率(縦軸)の散布図は $\boxed{\text{ サ }}$ である。
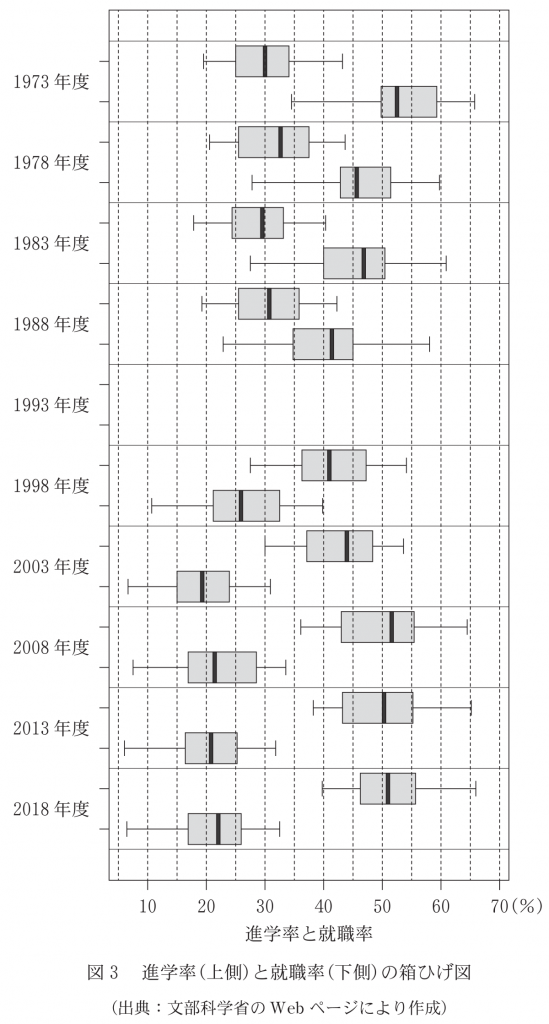
(2) 図 3 は,1973 年度から 2018 年度まで,5 年ごとの 10 個の年度(それぞれを時点という)における都道府県別の進学率(上側)と就職率(下側)を箱ひげ図で表したものである。ただし,設問の都合で 1993 年度における箱ひげ図は表示していない。
次の $\boxed{\text{ シ }}$ に当てはまるものを,下の⓪~④のうちから一つ選べ。
図 3 から読み取れることとして,正しい記述は $\boxed{\text{ シ }}$ である。
⓪ 1993 年度を除く 9 時点すべてにおいて,進学率の左側のひげの長さと右側のひげの長さを比較すると,右側の方が長い。
① 2003 年度,2008 年度,2013年度,2018 年度の 4 時点すべてにおいて,就職率の左側のひげの長さと右側のひげの長さを比較すると,左側の方が長い。
② 2003 年度,2008 年度,2013 年度,2018 年度の 4 時点すべてにおいて,就職率の四分位範囲は,それぞれの直前の時点より減少している。
③ 1993 年度を除く時点ごとに進学率と就職率の四分位範囲を比較すると,つねに就職率の方が大きい。
④ 就職率について,1993 年度を除くどの時点においても最大値は最小値の 2 倍以上である。
(3) 図 4 は,1993 年度における都道府県別の進学率(横軸)と就職率(縦軸)の散布図である。
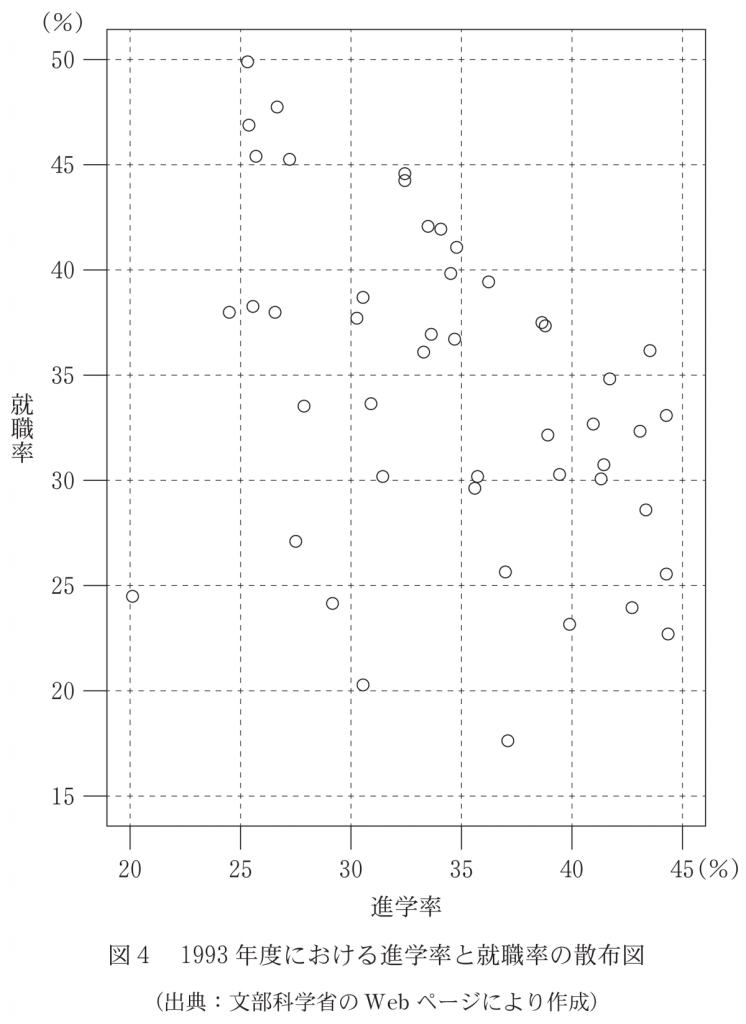
次の $\boxed{\text{ ス }}$,$\boxed{\text{ セ }}$ に当てはまる最も適当なものを,それぞれの解答群から一つずつ選べ。
1993 年度における就職率の $\boxed{\text{ ス }}$ は 34.8%である。
また,1993 年度における進学率の $\boxed{\text{ ス }}$ は $\boxed{\text{ セ }}$ %である。
$\boxed{\text{ ス }}$ の解答群
⓪ 最小値 ① 中央値 ② 最大値
③ 第1四分位数 ④ 第3四分位数
⑤ 四分位範囲
$\boxed{\text{ セ }}$ の解答群
⓪ 10.0 ① 20.1 ② 29.7
③ 34.5 ④ 39.7 ⑤ 44.4
(4) 図 4 に示した 1993 年度における都道府県別の進学率と就職率の相関係数を計算したところ,$-0.41$ であった。就職率が 45 %を超えている 5 都道府県を黒丸で示したのが図 5 である。 次の $\boxed{\text{ ソ }}$ に当てはまるものを,下の⓪~⑤のうちから一つ選べ。
就職率が 45 %を超えている 5 都道府県を除外したときの相関係数を $r$ とおくと,$\boxed{\text{ ソ }}$ である。
⓪ $r<-0.41$ ① $r=-0.41$
② $-0.41< r < 0$ ③ $r=0$
④ $0 < r < 0.41$ ⑤ $r\geqq0.41$
(5) 1993 年度における進学率 $X$,就職率 $Y$ について,$X$ の平均値の 2 乗の値を求めたい。$X^2$ の平均値,$Y$ の平均値と標準偏差,$X$ と $Y$ の共分散と相関係数は表 1 のとおりであった。ただし,$X$ と $Y$ の共分散とは,$X$ の偏差と $Y$ の偏差の積の平均値である。なお,表 1 の数値は正確な値であり,四捨五入されていないものとする。
また,必要であれば以下の事実を用いてもよい。
$n$ を自然数とする。実数値のデータ $u_1,u_2,\cdots,u_n$ に対して,平均値を $\bar{u}$,分散を $s^2$ とおくと
$s^2=\cfrac{{u_1}^2+{u_2}^2+\cdots+{u_n}^2}{n}-(\bar{u})^2$
が成り立つ。
$X$ の標準偏差は,小数第 2 位を四捨五入すると,$\boxed{\text{ タ }}$,$\boxed{\text{ チ }}$ である。
次の $\boxed{\text{ ツ }}$ に当てはまる数値として最も近いものを,下の⓪~⑦のうちから一つ選べ。
$X$ の平均値の 2 乗の値は $\boxed{\text{ ツ }}$ である。
⓪ 1122 ① 1156 ② 1182
③ 1223 ④ 1260 ⑤ 1296
⑥ 1332 ⑦ 1369
SNSでシェア