【スマホで読む・わかりやすい】センター数学IA2020本試【解説・正解・問題】

解答・解説

ア 1　イ ウ 1 8　エ オ 2 7

カ キク 9 56　ケコ 12　サシ 71

ス 2

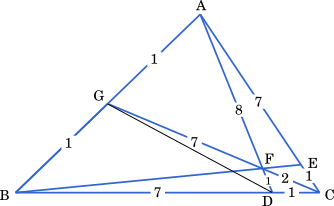
チェバの定理を用いて

$\cfrac{\text{AG}}{\text{GB}}\times\cfrac{\text{BD}}{\text{DC}}\times\cfrac{\text{CF}}{\text{FA}}=1$

$\cfrac{\text{AG}}{\text{GB}}\times\cfrac{7}{1}\times\cfrac{1}{7}=1$

$\cfrac{\text{GB}}{\text{AG}}=1$

・・・ア

メネラウスの定理を用いて

$\cfrac{\text{AG}}{\text{GB}}\times\cfrac{\text{BC}}{\text{CD}}\times\cfrac{\text{DF}}{\text{FA}}=1$

$\cfrac{1}{1}\times\cfrac{8}{1}\times\cfrac{\text{DF}}{\text{FA}}=1$

$\cfrac{\text{FD}}{\text{AF}}=\cfrac{1}{8}$

・・・イウ

メネラウスの定理を用いて

$\cfrac{\text{CD}}{\text{DB}}\times\cfrac{\text{BA}}{\text{AG}}\times\cfrac{\text{GF}}{\text{FC}}=1$

$\cfrac{1}{7}\times\cfrac{2}{1}\times\cfrac{\text{GF}}{\text{FC}}=1$

$\cfrac{\text{FC}}{\text{GF}}=\cfrac{2}{7}$

・・・エオ

次に，それぞれの三角形の面積の比を求めると

△CDG = △ABC $\times\cfrac{1}{2}$

△CDG = △BCG $\times\cfrac{1}{8}$

また

△BFG = △BCG $\times\cfrac{7}{9}$

したがって

$\cfrac{\text{△CDGの面積}}{\text{△BFGの面積}}=\cfrac{\enspace\cfrac{1}{8}\enspace}{\cfrac{7}{9}}=\cfrac{\enspace\cfrac{1}{8}\times72\enspace}{\cfrac{7}{9}\times72}=\cfrac{9}{56}$

・・・カキク

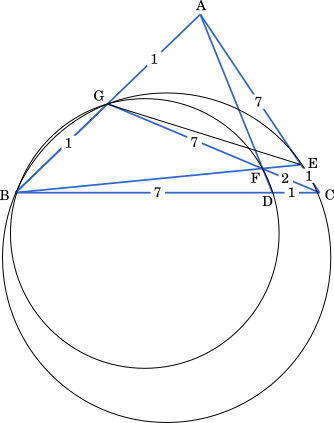
AB = $x$ とおいて，方べきの定理より

AF・AD = AG・AB

$8\times9=\cfrac{x}{2}\times x$

$x^2=144$

$x=12$

したがって AB = $12$

・・・ケコ

さらに，AE = $3\sqrt{7}$ とすると

AC = $3\sqrt{7}\times\cfrac{8}{7}=\cfrac{24\sqrt{7}}{7}$

AE・AC = $3\sqrt{7}\times\cfrac{24\sqrt{7}}{7}=72$

・・・サシ

また

AG・AB = $6\times12=72$

AE・AC = AG・AB だから，方べきの定理の逆より 4 点 B, C, E, G は同一円周上にある。よって，△AEB ∽ △ABC となり

∠AEG = ∠ABC

・・・ス

第5問

△ABCにおいて, 辺 BC を 7 : 1 に内分する点を D とし辺 AC を 7 : 1 に内分する点を E とする。線分 AD と線分 BE の交点を F とし, 直線 CF と辺 AB の交点を G とすると

$\cfrac{\text{GB}}{\text{AG}}=\boxed{\text{ア}}$, $\cfrac{\text{FD}}{\text{AF}}=\cfrac{\boxed{\text{イ}}}{\boxed{\text{ウ}}}$, $\cfrac{\text{FC}}{\text{GF}}=\cfrac{\boxed{\text{エ}}}{\boxed{\text{オ}}}$

である。したがって

$\cfrac{\text{△CDG の面積}}{\text{△BFG の面積}}=\cfrac{\boxed{\text{カ}}}{\boxed{\text{キク}}}$

となる。

4 点 B, D, F, G が同一円周上にあり,かつ FD = 1 のとき

AB = $\boxed{\text{ケコ}}$

である。さらに, AE = $3\sqrt{7}$ とするとき, AE・AC = $\boxed{\text{サシ}}$ であり

∠AEG = $\boxed{\text{ス}}$

である。$\boxed{\text{ス}}$ に当てはまるものを次の⓪~③のうちから一つ選べ。

⓪ ∠BGE　① ∠ADB

② ∠ABC　③ ∠BAD