【スマホで読む・わかりやすい】センター数学IA2020本試【解説・正解・問題】

第2問　解答・解説

ア 2　イウ 14　エ　4　オ 2　カ 1

キ 4　ク 7　ケ 7

コ,サ 3,5 または 5,3

シ 6　ス 4　セ 3

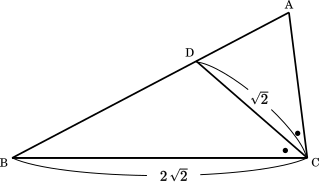
余弦定理を用いて

$\text{BD}^2=(2\sqrt{2})^2+(\sqrt{2})^2-2\cdot2\sqrt{2}\cdot\sqrt{2}\cos$∠BCD

$=8+2-8\cdot\cfrac{3}{4}$

$=4$

BD = $2$

・・・ア

次に，$\sin$∠ADC は直接求めることができない。しかし $\cos$∠BDC は求めることができるので，∠ADC = $180\degree$ – ∠BDC であることを利用するとよい。

余弦定理を用いて

$(2\sqrt{2})^2=2^2+(\sqrt{2})^2-2\cdot2\cdot\sqrt{2}\cos$∠BDC

$8=4+2-4\sqrt{2}\cos$∠BDC

$4\sqrt{2}\cos$∠BDC = $-2$

$\cos$∠BDC = $-\cfrac{2}{4\sqrt{2}}=-\cfrac{\sqrt{2}}{4}$

∠ADC = $180\degree-$∠BDC だから

$\cos(180\degree-$∠BDC$)=-\cos$∠BDC

$\cos$∠ADC$=-\cos$∠BDC

$\cos$∠ADC$=\cfrac{\sqrt{2}}{4}$

$\sin^2 x+\cos^2 x=1$ を用いて

$\sin^2$∠ADC$+\bigg(\cfrac{\sqrt{2}}{4}\bigg)^2=1$

$\sin^2$∠ADC$=\cfrac{7}{8}$

$\sin$∠ADC$=\sqrt{\cfrac{7}{8}}$

$=\cfrac{\sqrt{7}}{2\sqrt{2}}=\cfrac{\sqrt{14}}{4}$

・・・イウエ

さらに角二等分線の性質より

AC : BC = AD : DB

AC : $2\sqrt{2}$ = AD : $2$

$2\sqrt{2}$AD=$2$AC

$\cfrac{\text{AC}}{\text{AD}}=\sqrt{2}$

・・・オ

ここで AD = $x$ とおくと

$\cfrac{\text{AC}}{x}=\sqrt{2}$

AC = $\sqrt{2}x$

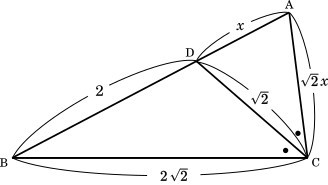
∠BCD = ∠ACD だから

$\cos$∠ACD = $\cfrac{3}{4}$

余弦定理を用いて

$x^2=(\sqrt{2})^2+(\sqrt{2})^2-2\cdot\sqrt{2}x\cdot\sqrt{2}\cdot\cfrac{3}{4}$

$x^2=2x^2+2-3x$

$x^2-3x+2=0$

$(x-1)(x-2)=0$

$x=1,2$

ここで $x=2$ とすると △ABC は二等辺三角形となり，CD は AB の垂直二等分線となる。しかし，その場合 $\sin$∠ADC = $1$ となるので成り立たない。よって，$x=1$ である。

したがって AD = $1$

・・・カ

これより，AC = $\sqrt{2}$ となる。

また，△ABC の外接円の半径を求めると，正弦定理を用いて

$2R=\cfrac{2\sqrt{2}}{\sin\text{∠BAC}}$

$=\cfrac{\enspace2\sqrt{2}\enspace}{\cfrac{\sqrt{14}}{4}}=\cfrac{\enspace2\sqrt{2}\times4\enspace}{\cfrac{\sqrt{14}}{4}\times4}$

$=\cfrac{8\sqrt{2}}{\sqrt{14}}=\cfrac{8}{\sqrt{7}}$

$=\cfrac{8\sqrt{7}}{7}$

$R=\cfrac{4\sqrt{7}}{7}$

・・・キクケ

〔2〕

(1)

⓪ 平均値は最小値と最大値の間でいかなる値も取り得るので，正しくない。

① 四分位範囲と標準偏差は性質の異なるものであり，比べることはできない。

③ 99 個のデータで中央値をとる場合，データは値の小さい順に 1~49, 50, 51~99 番目に分ける。このとき，50 番目が中央値である。したがって，正しい。

④ データを四分位で分ける場合，1~24, 25, 26~49, 50, 51~74, 75, 76~99 番目に分ける。このとき 25 番目が第1四分位数，50 番目が中央値， 75 番目が第3四分位数である。したがって，第1四分位数より小さい観測値と，第3四分位数より大きい観測値とをすべて削除すると，残りの観測値は $99-24-24=51$ 個となる。ただしこれはデータに重複がない場合であって，重複がある場合には四分位数の値が変わるため，正しくない。

⑤ 四分位範囲とは第3四分位数から第1四分位数を引いたものであり，第1四分位数より小さい観測値と，第3四分位数より大きい観測値をすべて削除したものに等しい。したがって，正しい。

・・・コサ

(2)

(I) P10 は四分位範囲が 1 以上である。したがって，誤。

(II) P10 の中央値は P11 より大きい。したがって，誤。

(III) 正しい。

・・・シ

(3)

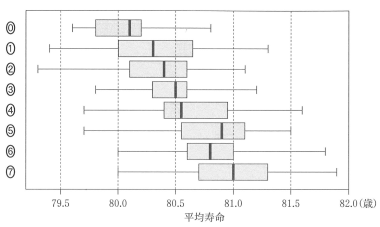
図2 より，最小値は 79.5 以上であるため，①，②は不適。次に，中央値は値の少ない順から数えて 10 番目と 11 番目の値の平均であり，80.5 ~ 81.0 の間にあるので，⓪ は不適。また，第1四分位数は 5 番目 と 6 番目の値の平均であり，80.0 ~ 80.5 の間にあるので，⑤，⑥，⑦ は不適。さらに，最大値は 81.5 ~ 82.0 の間にあるので ③ は不適。したがって，④ が適する。

・・・ス

(4)

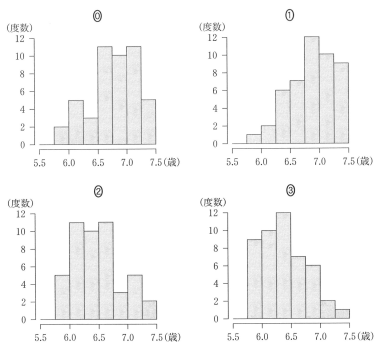
散布図の原点から伸びる直線は男女の平均寿命がちょうど 7 歳差であることを示す。また，この直線より左上にあるデータは平均寿命の差が 7 歳以上であることを示しており，3 つの都道府県があることが分かる。これに当てはまるヒストグラムは ③。

・・・セ

第２問　問題

〔1〕△ABC において，BC = $2\sqrt{2}$ とする。∠ACB の二等分線と辺 AB の交点を D とし，CD = $\sqrt{2}$，$\cos$ ∠BCD = $\cfrac{3}{4}$ とする。このとき，BD = $\boxed{\text{ア}}$ であり

$\sin$ ∠ADC = $\cfrac{\sqrt{\boxed{\text{イウ}}}}{\boxed{\text{エ}}}$

である。$\cfrac{\text{AC}}{\text{AD}}=\sqrt{\boxed{\text{オ}}}$ であるから

AD = $\boxed{\text{カ}}$

である。また，△ABC の外接円の半径は $\cfrac{\boxed{\text{キ}}\sqrt{\boxed{\text{ク}}}}{\boxed{\text{ケ}}}$ である。

〔2〕

(1) 次の $\boxed{\text{コ}}$，$\boxed{\text{サ}}$ に当てはまるものを，下の ⓪~⑤ のうちから一つずつ選べ。ただし，解答の順序は問わない。

99 個の観測値からなるデータがある。四分位数に述べた記述で，どのようなデータでも成り立つものは $\boxed{\text{コ}}$ と $\boxed{\text{サ}}$ である。

⓪ 平均値は第 1 四分位数と第 3 四分位数の間にある。

① 四分位範囲は標準偏差より大きい。

② 中央値より小さい観測地の個数は 49 個である。

③ 最大値に等しい観測地を 1 個削除しても第 1 四分位数は変わらない。

④ 第 1 四分位数より小さい観測地と，第 3 四分位数より大きい観測値とをすべて削除すると，残りの観測値からなるデータの範囲はもとのデータの四分位範囲に等しい。

(2) 図 1 は，平成 27 年の男の市区町村別平均寿命のデータを 47 の都道府県 P1，P2, …, P47 ごとに箱ひげ図にして，並べたものである。

次の(I), (II), (III)は図 1 に関する記述である。

(I) 四分位範囲はどの都道府県においても 1 以下である。

(II) 箱ひげ図は中央値が小さい値から大きい値の順に上から下へ並んでいる。

(III) P1 のデータのどの値と P47 のデータのどの値とを比較しても 1.5 以上の差がある。

次の $\boxed{\text{シ}}$ に当てはまるものを,下の ⓪~⑦のうちから一つ選べ。

(I), (II), (III)の正誤の組合せとして正しいものは、$\boxed{\text{シ}}$ である。

	⓪	①	②	③	④	⑤	⑥	⑦
(I) (II) (III)	正 正 正	正 正 誤	正 誤 正	誤 正 正	正 誤 誤	誤 正 誤	誤 誤 正	誤 誤 誤

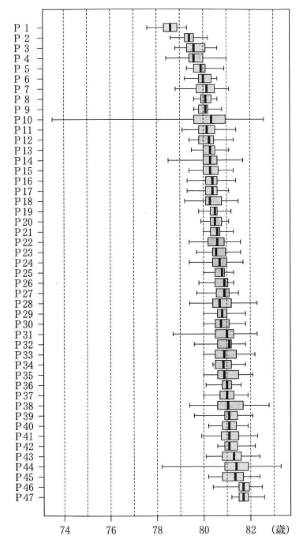
図1 男の市区町村別平均寿命の箱ひげ図 (出典:厚生労働省の Web ページにより作成)

(3) ある県は 20 の市区町村からなる。図2はその県の男の市区町村別平均寿命のヒストグラムである。なお,ヒストグラムの各階級の区間は,左側の数値を含み,右側の数値を含まない。

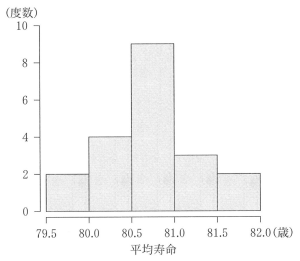
図2 市区町村別平均寿命のヒストグラム (出典:厚生労働省の Web ページにより作成)

次の $\boxed{\text{ス}}$ に当てはまるものを,下の ⓪~⑦ のうちから一つ選べ。

図2のヒストグラムに対応する箱ひげ図は $\boxed{\text{ス}}$ である。

(4) 図 3 は、平成 27 年の男の都道府県別平均寿命と女の都道府県別平均寿命の散布図である。2 個の点が重なって区別できない所は黒丸にしている。図には補助的に切片が 5.5 から 7.5 まで 0.5 刻みで傾き 1 の直線を 5 本付加している。

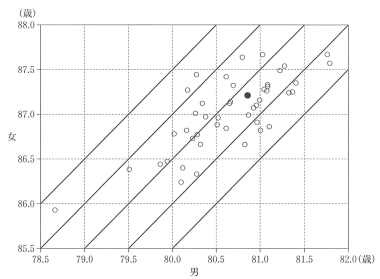
図3 男と女の都道府県別平均寿命の散布図
(出典:厚生労働省のWeb ページにより作成)

次の $\boxed{\text{セ}}$ に当てはまるものを, 下の⓪~③のうちから一つ選べ。

都道府県ごとに男女の平均寿命の差をとったデータに対するヒストグラムは，$\boxed{\text{セ}}$ である。なお, ヒストグラムの各階級の区間は, 左側の数値を含み, 右側の数値を含まない。