【スマホで読む・わかりやすい】センター数学IA2020本試【解説・正解・問題】
第1問 解答・解説
アイ -2 ウ 4 エ 0 オ 4
カキ -2
ク 5 ケ 3 コ 6 サシ 13
ス 2 セソ 12 タ 4 チ 3
ツ 2 テ 4 ト 1 ナ 0
ニ 2 ヌ 3 ネ 3 ノ 3
ハヒ -4
フ 8 ヘ 6 ホ 3
〔1〕
(1)
$\ell:y=(a^2-2a-8)x+a$
傾きが負のとき
$a^2-2a-8\lt0$
$(a+2)(a-4)\lt0$
$-2\lt a\lt 4$
・・・アイウ
(2)
$\ell$ の切片は $a$ である。$a\gt0$ つまり $a$ が正の値のとき, $0\lt a \lt 4$ の範囲では傾きは負の値をとる。

また,$a\gt4$ のとき,傾きは正の値をとる。

よって,$b\gt0$ となるのは $0\lt a \lt 4$ のときである。
また,$a\leqq0$ つまり $a$ が負の値のとき,$-2\lt a\leqq0$ の範囲では傾きは負の値をとる。

また,$a\lt-2$ のとき,傾きは正の値をとる。

よって,$b\gt0$ となるのは $a\lt2$ のときである。
・・・エオ
さらに,$a=\sqrt{3}$ のとき,$b$ の値を求める。$b$ は $y=0$ のときの $x$ の値だから,これらを $\ell$ に代入すると
$\{(\sqrt{3})^2-2\sqrt{3}-8\}x+\sqrt{3}=0$
$(-5-2\sqrt{3})x+\sqrt{3}=0$
$x=\cfrac{\sqrt{3}}{5+2\sqrt{3}}$
分母を有理化して
$=\cfrac{\sqrt{3}(5-2\sqrt{3})}{(5+2\sqrt{3})(5-2\sqrt{3})}$
$=\cfrac{5\sqrt{3}-6}{25-12}$
$=\cfrac{5\sqrt{3}-6}{13}$
したがって $b=\cfrac{5\sqrt{3}-6}{13}$
・・・クケコサシ
〔2〕
(1)
32 は 4 の倍数であるが,6 の倍数でも 24 の倍数でもない。したがって,選択肢の中で当てはまるものは
$32\in P\cap \overline{Q}$
・・・ス
(2)
$P\cap Q$ は 4 の倍数かつ 6 の倍数,つまり公倍数である。この中で最小のもの,つまり最小公倍数は 12 である。
・・・セソ
12 は R,つまり 24 の倍数に含まれない。したがって
$12\notin R$
・・・タ
(3)
(2)より自然数 12 がそれぞれの命題の反例になるかどうかを考える。
⓪ ( $p$ かつ $q$ ) は 4 と 6 の公倍数,つまり 12 の倍数であり 12 を含む。また $\overline{r}$ は 24 の倍数以外であるから 12 を含む。したがって 12 は反例にならない。
① ( $p$ または $q$ ) は 4 の倍数と 6 の倍数のいずれかであり 12 を含む。したがって ⓪ と同様に $\overline{r}$ に 12 が含まれるので反例にならない。
② $r$ は 24 の倍数であり,( $p$ かつ $q$ ) は 12 の倍数である。したがって命題が成り立つので 12 は反例にならない。
③ ( $p$ かつ $q$ ) は 12 の倍数で 12 を含むが,$r$ は 24 の倍数で 12 を含まない。したがって 12 は反例となる。
・・・チ
〔3〕
(1)
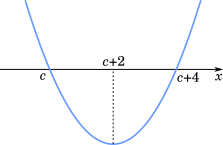
頂点の $x$ 座標は $c+2$ となるので,$G$ は
$y=\{x-(c+2)\}^2+k$
と表すことができる。$G$ は $(c,0)$ を通るのでこれを代入して
$\{c-(c-2)\}^2+k=0$
$k=-4$
よって
$G:y=\{x-(c+2)\}^2-4$
$=x^2-2(c+2)x+(c+2)^2-4$
$=x^2-2(c+2)x+c^2+4c+4-4$
$=x^2-2(c+2)x+c(c+4)$
・・・ツテ
次に,2 点 $(3,0),(3,-3)$ を両端とする線分を $G$ が共有点をもつような $c$ の範囲を求めると
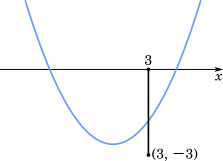
$x=3$ で $-3\leqq y\leqq0$ であればよい。
$G$ に $x=3$ を代入すると
$y=9-2(c+2)3+c(c+4)$
$=9-6c-12+c^2+4c$
$=c^2-2c-3$
よって
$-3\leqq c^2-2c-3\leqq0$
ここで $-3\leqq c^2-2c-3$ とすると
$c^2-2c\geqq0$
$c(c-2)\geqq0$
$c\leqq0$, $c\geqq2$
また $c^2-2c-3\leqq0$ とすると
$(c+1)(c-3)\leqq0$
$-1\leqq c\leqq 3$

したがって
$-1\leqq c \leqq 0$,$2\leqq c\leqq 3$
・・・トナニヌ
(2)
$2\leqq c\leqq 3$ のとき
$G:y=\{x-(c+2)\}^2-4$ に $(3,-1)$ を代入して
$\{3-(c+2)\}^2-4=-1$
$(1-c)^2-4=-1$
$c^2-2c+1-4=-1$
$c^2-2c-2=0$
$c=1\pm\sqrt{3}$
このうち,$2\leqq c\leqq3$ に当てはまるのは $1+\sqrt{3}$
よって $c=1+\sqrt{3}$
頂点の $x$ 座標は $c+2$ だから $3+\sqrt{3}$ となる。したがって,$G$ は $y=x^2$ のグラフを $x$ 軸方向に $3+\sqrt{3}$,$y$ 軸方向に $-4$ だけ平行移動したものである。
・・・ネノハヒ
このとき $G$ と $y$ 軸との交点の $y$ 座標を求めると,$x=0$ のときだから $G$ に代入して
$y=c(c+4)$
$=(1+\sqrt{3})(1+\sqrt{3}+4)$
$=(1+\sqrt{3})(5+\sqrt{3})$
$=8+6\sqrt{3}$
・・・フヘホ
第1問 問題文
〔1〕$a$ を定数とする。
(1) 直線 $\ell:y=(a^2-2a-8)x+a$ の傾きが負となるのは,$a$ の値の範囲が
$\boxed{\text{アイ}}\lt a\lt\boxed{\text{ウ}}$
のときである。
(2) $a^2-2a-8\not=0$ とし,(1)の直線 $\ell$ と $x$ 軸との交点の $x$ 座標を $b$ とする。
$a\gt0$ の場合,$b\gt0$ となるのは $\boxed{\text{エ}}\lt a\lt\boxed{\text{オ}}$ のときである。
$a\leqq0$ の場合,$b\gt0$ となるのは $a\lt\boxed{\text{カキ}}$ のときである。
また,$a=\sqrt{3}$ のとき
$b=\cfrac{\boxed{\text{ク}}\sqrt{\boxed{\text{ケ}}}-\boxed{\text{コ}}}{\boxed{\text{サシ}}}$
である。
〔2〕自然数 $n$ に関する三つの条件 $p,q,r$ を次のように定める。
$p:n$ は $4$ の倍数である
$q:n$ は $6$ の倍数である
$r:n$ は $24$ の倍数である
条件 $p,q,r$ の否定をそれぞれ $\overline{p},\overline{q},\overline{r}$ で表す。
条件 $p$ を満たす自然数全体の集合を $P$ とし,条件 $q$ を満たす自然数全体の集合を $Q$ とし,条件 $r$ を満たす自然数全体の集合を $R$ とする。自然数全体の集合を全体集合とし,集合 $P,Q,R$ の補集合をそれぞれ $\overline{P},\overline{Q},\overline{R}$ で表す。
(1) 次の $\boxed{\text{ス}}$ に当てはまるものを,下の⓪~⑤のうちから一つ選べ。
$32\in\boxed{\text{ス}}$ である。
⓪ $P\cap Q\cap R$ ① $P\cap Q\cap\overline{R}$
② $P\cap\overline{Q}$ ③ $\overline{P}\cap Q$
④ $\overline{P}\cap\overline{Q}\cap R$ ⑤ $\overline{P}\cap\overline{Q}\cap\overline{R}$
(2) 次の $\boxed{\text{タ}}$ に当てはまるものを,下の⓪~④のうちから一つ選べ。
$P\cap Q$ に属する自然数のうち最小のものは $\boxed{\text{セソ}}$ である。
⓪ $=$ ① $\subset$
② $\supset$ ③ $\in$
④ $\notin$
(3) 次の$\boxed{\text{チ}}$に当てはまるものを,下の⓪~③のうちから一つ選べ。
自然数$\boxed{\text{セソ}}$は,命題$\boxed{\text{チ}}$の反例である。
⓪ 「($p$ かつ $q$)$\implies\overline{r}$」
① 「($p$ または $q$)$\implies\overline{r}$」
② 「$r\implies$($p$ かつ $q$ )」
③ 「($p$ かつ $q$)$\implies r$」
〔3〕 $c$ を定数とする。2 時間数 $y=x^2$ のグラフを,2 点 $(c,0)$,$(c+4,0)$ を通るように平行移動して得られるグラフを $G$ とする。
(1) $G$ をグラフに持つ 2 時間数は,$c$ を用いて
$y=x^2-2(c+\boxed{\text{ツ}})x+c(c+\boxed{\text{テ}})$
と表せる。
2 点 $(3,0)$,$(3,-3)$ を両端とする線分と $G$ が共有点を持つような $c$ の値の範囲は
$-\boxed{\text{ト}}\leqq c\leqq\boxed{\text{ナ}}$,$\boxed{\text{ニ}}\leqq c\leqq\boxed{\text{ヌ}}$
である。
(2) $\boxed{\text{ニ}}\leqq c\leqq\boxed{\text{ヌ}}$ の場合を考える。$G$ が点 $(3,-1)$ wp通るとき,$G$ は 2 次関数 $y=x^2$ のグラフを $x$ 軸方向に $\boxed{\text{ネ}}+\sqrt{\boxed{\text{ノ}}}$,$y$ 軸方向に $\boxed{\text{ハヒ}}$ だけ平行移動したものである。また,このとき $G$ と $y$ 軸との交点の $y$ 座標は $\boxed{\text{フ}}+\boxed{\text{ヘ}}\sqrt{\boxed{\text{ホ}}}$ である。
SNSでシェア