【スマホで読む・わかりやすい】センター数学IA2019追試【解説・正解・問題】

第5問　正解と解説

ア 4　イ ウ エ 2 6 3　オ カ 2 3
キク ケ 51 3　コサ シ 51 5
スセ ソタ 51 51　チ 4　ツ テ 5 2

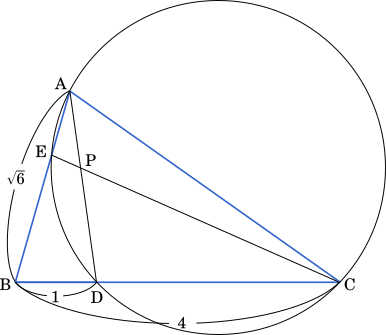
方べきの定理より

BE・BA ＝ BD・BC

＝ 1・4 ＝ 4

・・・ア

BE・$\sqrt{6}$ ＝ 4

BE ＝ $\cfrac{4}{\sqrt{6}}=\cfrac{2\sqrt{6}}{3}$

・・・イウエ

メネラウスの定理より

$\cfrac{\text{AE}}{\text{EB}}\cdot\cfrac{\text{BC}}{\text{CD}}\cdot\cfrac{\text{DP}}{\text{PA}}=1$

ここで

$\cfrac{\text{AE}}{\text{EB}}=\cfrac{\sqrt{6}-\cfrac{2\sqrt{6}}{3}}{\cfrac{2\sqrt{6}}{3}}=\cfrac{\Big(\sqrt{6}-\cfrac{2\sqrt{6}}{3}\Big)\times3}{\cfrac{2\sqrt{6}}{3}\times3}$

$=\cfrac{3\sqrt{6}-2\sqrt{6}}{2\sqrt{6}}=\cfrac{\sqrt{6}}{2\sqrt{6}}$

$=\cfrac{1}{2}$

だから

$\cfrac{1}{2}\cdot\cfrac{4}{3}\cdot\cfrac{\text{DP}}{\text{PA}}=1$

$\cfrac{\text{DP}}{\text{PA}}=\cfrac{3}{2}$

$\cfrac{\text{AP}}{\text{PD}}=\cfrac{2}{3}$

・・・オカ

よって AP：PD ＝ 2 ： 3

余弦定理より

$\text{AD}^2=(\sqrt{6})^2+1^2-2\cdot\sqrt{6}\cdot1\cdot\cos$∠ABC

$=6+1-2\sqrt{6}\cdot\cfrac{\sqrt{6}}{9}$

$=7-\cfrac{12}{9}=\cfrac{17}{3}$

よって

AD ＝ $\sqrt{\cfrac{17}{3}}=\cfrac{\sqrt{51}}{3}$

・・・キクケ

AP：PD ＝ 2 ： 3 より

PD ＝ $\cfrac{\sqrt{51}}{3}\cdot\cfrac{3}{5}=\cfrac{\sqrt{51}}{5}$

・・・コサシ

余弦定理より

$(\sqrt{6})^2=1^2+\Big(\cfrac{\sqrt{51}}{3}\Big)^2-2\cdot1\cdot\cfrac{\sqrt{51}}{3}\cos$∠ADB

$6=1+\cfrac{51}{9}-\cfrac{2\sqrt{51}}{3}\cos$∠ADB

$\cfrac{2\sqrt{51}}{3}\cos$∠ADB ＝ $1+\cfrac{51}{9}-6=\cfrac{2}{3}$

$\cos$∠ADB ＝ $\cfrac{2}{3}\cdot\cfrac{3}{\sqrt{51}}$

$=\cfrac{1}{\sqrt{51}}=\cfrac{\sqrt{51}}{51}$

・・・スセソタ

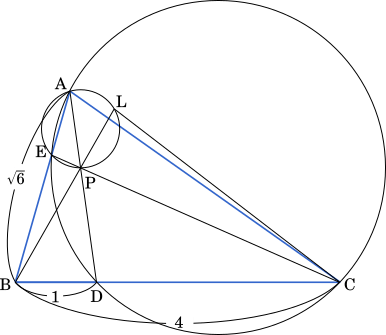
方べきの定理より

BP・BL ＝ BE・BA

＝ $\cfrac{2\sqrt{6}}{3}\cdot\sqrt{6}=4$

・・・チ

BD・BC ＝ 4 だから

BP・BL ＝ BD・BC が成り立つ。

よって，CDPL は同一円周上にある。

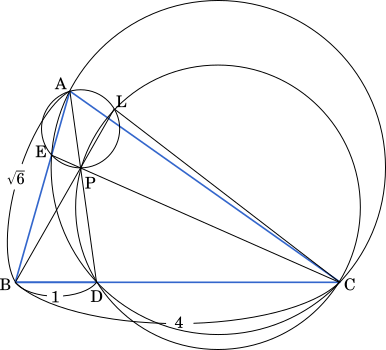
よって

∠CDP＋∠CLP ＝ 180°

$\cos$∠ADB ＝ $\cfrac{\sqrt{51}}{51}$ だから

$\cos$∠CDP ＝ $-\cfrac{\sqrt{51}}{51}$

$\cos$∠BLC ＝ $\cfrac{\sqrt{51}}{51}$

三角比の公式 $1+\tan^2x=\cfrac{1}{\cos^2x}$ より

$1+\tan^2$∠BLC ＝ $\cfrac{1}{\cos^2\angle\text{BLC}}$

$=\cfrac{1}{\Big(\cfrac{\sqrt{51}}{51}\Big)^2}=\cfrac{1}{\space\cfrac{1}{51}\space}$

$=\cfrac{1\times51}{\space\cfrac{1}{51}\times51\space}=51$

$\tan^2$∠BLC ＝ 50

$\tan$∠BLC ＝ $5\sqrt{2}$

・・・ツテ

問題文

△ABC において, AB＝$\sqrt{6}$, BC＝4, $\cos$∠ABC＝$\cfrac{\sqrt{6}}{9}$ とする。

辺 BC 上の点 D を BD ＝ 1 となるようにとり, △ACD の外接円と辺 AB の交点で, 点 A とは異なる点を E とする。このとき

BE・BA = $\boxed{\text{ア}}$

であるから, BE＝$\cfrac{\boxed{\text{イ}}\sqrt{\boxed{\text{ウ}}}}{\boxed{\text{エ}}}$ である。

線分 AD と線分 EC の交点を P とすると

$\cfrac{\text{AP}}{\text{PD}}=\cfrac{\boxed{\text{オ}}}{\boxed{\text{カ}}}$

である。AD＝$\cfrac{\sqrt{\boxed{\text{キク}}}}{\boxed{\text{ケ}}}$ であるから, PD＝$\cfrac{\sqrt{\boxed{\text{コサ}}}}{\boxed{\text{シ}}}$ である。また, $\cos$∠ADB＝$\cfrac{\sqrt{\boxed{\text{スセ}}}}{\boxed{\text{ソタ}}}$ である。

次に, △AEP の外接円と直線 BP の交点で, 点 P とは異なる点を L とする。

BP・BL＝$\boxed{\text{チ}}$

である。

BD · BC ＝ 4

であるから, $\tan$ ∠BLC＝$\boxed{\text{ツ}}\sqrt{\boxed{\text{テ}}}$ である。