【スマホで読む・わかりやすい】センター数学IA2019追試【解説・正解・問題】

第2問　正解と解説

アイ 12　ウ エ 2 3　オ 8　カキ 12
ク ケコ 2 17　サ 3　シ 2　ス 0
セ 0　ソ 6　タ 7

〔1〕

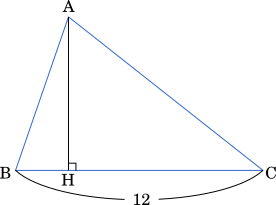
A から BC に下ろした垂線と BC の交点を H とすると

AB・$\cos$∠ABC ＝ BH

AC・$\cos$∠ACB ＝ CH

よって

AB・$\cos$∠ABC＋AC・$\cos$∠ACB

＝ BH ＋ CH ＝ 12

・・・アイ

正弦定理より

$\cfrac{\text{AC}}{\sin\angle\text{ABC}}=\cfrac{\text{AB}}{\sin\angle\text{ACB}}$

$\cfrac{\text{AB}}{\text{AC}}=\cfrac{\sin\angle\text{ACB}}{\sin\angle\text{ABC}}$

ここで $\sin^2x+\cos^2x=1$ より

$\sin^2$∠ABC＋$\Big(\cfrac{1}{3}\Big)^2=1$

$\sin^2$∠ABC＝$\cfrac{8}{9}$

$\sin$∠ABC＝$\sqrt{\cfrac{8}{9}}$

$=\cfrac{2\sqrt{2}}{3}$

また

$\sin^2$∠ACB＋$\Big(\cfrac{7}{9}\Big)^2=1$

$\sin^2$∠ACB＝$\cfrac{32}{81}$

$\sin$∠ACB＝$\cfrac{4\sqrt{2}}{9}$

よって

$\cfrac{\text{AB}}{\text{AC}}=\cfrac{\space\cfrac{4\sqrt{2}}{9}}{\cfrac{2\sqrt{2}}{3}}=\cfrac{\space\cfrac{4\sqrt{2}}{9}\times9}{\cfrac{2\sqrt{2}}{3}\times9}$

$=\cfrac{4\sqrt{2}}{6\sqrt{2}}=\cfrac{2}{3}$

・・・ウエ

よって AB：AC＝2：3

AB ＝ $x$ とおくと AC ＝ $\cfrac{3}{2}x$

これらを AB・$\cos$∠ABC＋AC・$\cos$∠ACB ＝ 12 に代入すると

$x\cdot\cfrac{1}{3}+\cfrac{3}{2}x\cdot\cfrac{7}{9}=12$

$\cfrac{x}{3}+\cfrac{7}{6}x=12$

$2x+7x=72$

$9x=72$

$x=8$

また

AC ＝ $\cfrac{3}{2}x$ ＝ $\cfrac{3}{2}\cdot8=12$

したがって AB ＝ 8，AC ＝ 12

・・・オカキ

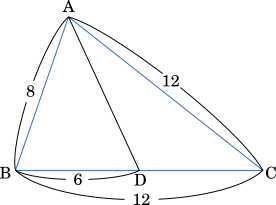
BC の中点を D とすると BD ＝ 6 だから，余弦定理より

$\text{AD}^2=8^2+6^2-2\cdot8\cdot6\cos$∠ABC

$=64+36-96\cdot\cfrac{1}{3}$

$=100-32=68$

AD ＝ $2\sqrt{17}$

・・・クケコ

〔2〕(1)

中央値は値の少ないものから数えて 24 番目だから，40 以上 44 未満に含まれる。よって③が正しい。

〔2〕(2)

(I) 1996年から2009年までは全体としては増加する傾向にある。よって正しい。

(II) 最大が最も大きいのは2011年の 15 であり，最大値が最も小さいのは1996年の 11 以上 12 未満である。よって最大値の差は 2 以上だから誤り。

(III) 第1四分位数は少ないものから数えて 12 番目である。1996年の中央値は 8 以上 9 未満に含まれるので，$Y$ が 9 以下のデータは少なくとも 24 個ある。また2014年は第1四分位数が 9 以上 10 未満に含まれるので，$Y$ が 9 以下のデータは多くても 12 個である。よって正しい。

・・・シ

〔2〕(3)

残布図より，$Y$ の最低値は 7 以上 8 未満だから③は不適。また最高値は 13 以上 14 未満だから①は不適。さらに散布図より，8 以上 9 未満のデータは 8 個だから，⓪が適する。

・・・ス

〔2〕(4)

$y-\overline{y}=\cfrac{s_{XY}}{{s_X}^2}(x-\overline{x})$ に値を代入すると

$y-10.2=\cfrac{1.75}{4.8}(x-9.6)$

$y-10.2=0.36x-3.46$

$y=0.36x+6.74$

・・・セソ

また $x=4$ のとき

$y=0.36\cdot4+6.74=8.18$

・・・タ

問題文

〔1〕△ABC において，BC＝12，$\cos$∠ABC＝$\cfrac{1}{3}$，$\cos$∠ACB＝$\cfrac{7}{9}$ とする。このとき

AB・$\cos$∠ABC＋AC・$\cos$∠ACB＝$\boxed{\text{アイ}}$，$\cfrac{\text{AB}}{\text{AC}}=\cfrac{\boxed{\text{ウ}}}{\boxed{\text{エ}}}$

である。

したがって

AB＝$\boxed{\text{オ}}$，AC＝$\boxed{\text{カキ}}$

であり，辺 BC の中点を D とすると AD＝$\boxed{\text{ク}}\sqrt{\boxed{\text{ケコ}}}$ ある。

〔2〕 疾病 A に関するいくつかのデータについて考える。

(1) 図 1 は, 47 都道府県の 40 歳以上 69 歳以下を対象とした「疾病 A の検診の受診率」のヒストグラムである。なお, ヒストグラムの各階級の区間は, 左側の数値を含み, 右側の数値を含まない。

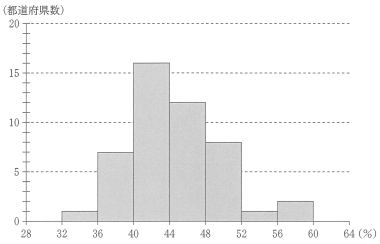
図1 疾病 A の検診の受診率のヒストグラム
(出典：国立がん研究センター Web ページにより作成)

次の $\boxed{\text{サ}}$ に当てはまるものを, 下の⓪~⑤のうちから一つ選べ。

疾病 A の検診の受診率の中央値として図 1 のヒストグラムと矛盾しないものは $\boxed{\text{サ}}$ である。

⓪ 16.0　① 24.0　② 35.6

③ 43.4　⑤ 44.7　⑥ 46.0

(2) 疾病 A の「調整済み死亡数」が毎年, 都道府県ごとに算出されている。なお, この調整済み死亡数は年齢構成などを考慮した 10 万人あたりの死亡数であり, 例えば 5.3 のように小数になることもある。

図 2 は, 各都道府県の疾病 A による調整済み死亡数 $Y$ を, 年ごとに箱ひげ図にして並べたものである。

図 2 に関する次の記述(I), (II), (III)について正誤を判定する。

(I) 1996 年から 2009 年までの間における各年の $Y$ の中央値は, 前年より小さくなる年もあるが, この間は全体として増加する傾向にある。

(II) $Y$ の最大値が最も大きい年と $Y$ の最大値が最も小さい年とを比べた場合, これら二つの年における最大値の差は 2 以下である。

(III) 1996 年と 2014 年で, $Y$ が 9 以下の都道府県数を比べると, 2014 年は 1996 年の 3 以下である。

次の $\boxed{\text{シ}}$ に当てはまるものを, 下の⓪~⑦のうちから一つ選べ。

(I), (II), (III)の記述の正誤について正しい組合せは, $\boxed{\text{シ}}$ である。

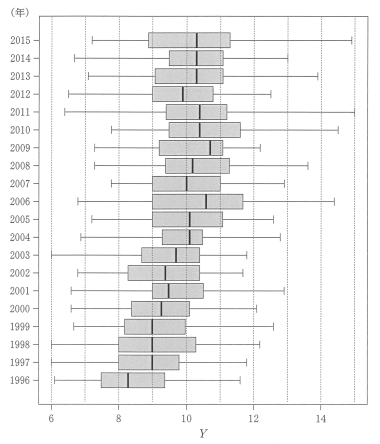
図2　年ごとの調整済み死亡数 $Y$ の箱ひげ図
(出典：国立がん研究センター Web ページにより作成)

(3) 図 3 は，ある年の 47 都道府県の喫煙率 $X$ と同じ年の調整済み死亡数 $Y$ との関係を表している。

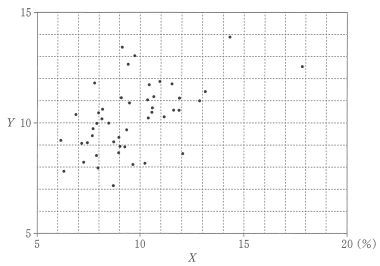
図3 喫煙率 $X$ と調整済み死亡数 $Y$ の散布図
(出典：国立がん研究センター Web ページにより作成)

次の $\boxed{\text{ス}}$ に当てはまるものを, 下の⓪~③のうちから一つ選べ。

$Y$ のヒストグラムとして最も適切なものは $\boxed{\text{ス}}$ である。

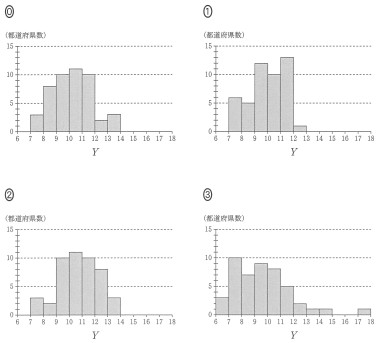
(4) 表 1 は，図 3 に表されている喫煙率 $X$ と調整済み死亡数 $Y$ の平均値，分散および共分散を計算したものである。ただし, 共分散とは「$X$ の偏差と $Y$ の偏差の積の平均値」である。なお, 表 1 の数値は四捨五入していない正確な値とする。

表1 平均値,分散,共分散

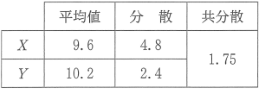
喫煙率 $X$ のとる値を $x$, 調整済み死亡数 $Y$ のとる値を $y$ とする。次の $x$ と $y$ の関係式(＊)はデータの傾向を知るためによく使われる式である。

$y-\overline{y}$＝$\cfrac{s_{XY}}{{s_X}^2}(x-\overline{x})\cdots\cdots$(＊)

ここで, $\overline{x}$, $\overline{y}$ はそれぞれ $X$, $Y$ の平均値, ${s_x}^2$ は $X$ の分散, $s_{xy}$ は $X$ と $Y$ の共分散を表す。

次の $\boxed{\text{セ}}$, $\boxed{\text{ソ}}$, $\boxed{\text{タ}}$ それぞれに当てはまる数値として最も近いものを, 下の⓪~⑨のうちから一つずつ選べ。

図 3 の散布図に対する関係式(＊)は $y=\boxed{\text{セ}}x+\boxed{\text{ソ}}$ であり, 図 4 はこの関係式を図 3 に当てはめたものである。

喫煙率が 3 % から 20 % の間では同じ傾向があると考えたとき, 上で求めた式を用いると, 喫煙率が 4 % であれば調整済み死亡数は $\boxed{\text{タ}}$ である。

⓪ 0.36　① 0.53　② 0.80
③ 1.26　④ 2.77　⑤ 5.13
⑥ 6.74　⑦ 8.18　⑧ 8.87
⑨ 9.95

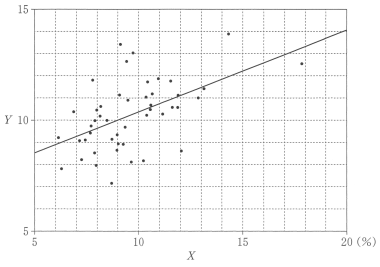
図4　図3に関係式を当てはめた図