【スマホで読む・わかりやすい】センター数学IA2019本試【解説・正解・問題】

第5問　解答・解説

ア イ 6 2　ウ 1　エ オカ キ 2 15 5

ク ケ 3 4　コ 3　サ シ 6 2

スセ ソ 15 5

三角形の内接円と面積の公式 $S=\cfrac{1}{2}(a+b+c)$ を用いるとよい。

まず，三角形の面積を $S=\cfrac{1}{2}bc\sin A$ を用いて求めると

$S=\cfrac{1}{2}\cdot4\cdot5\cdot\cfrac{2\sqrt{6}}{5}$

$=4\sqrt{6}$

$4\sqrt{6}=\cfrac{1}{2}r(4+7+5)=8r$

$r=\cfrac{\sqrt{6}}{2}$

・・・アイ

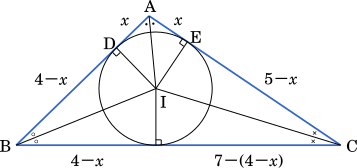
上の図のように AD ＝ $x$ とおくと

$7-(4-x)=5-x$

$3+x=5-x$

$2x=2$

$x=1$

したがって，AD ＝ 1

・・・ウ

また AE ＝ 1

△ADE において余弦定理より

$\text{DE}^2=1^2+1^2-2\cdot1\cdot1\cdot\Big(-\cfrac{1}{5}\Big)$

$=2+\cfrac{2}{5}=\cfrac{12}{5}$

DE ＝ $\cfrac{2\sqrt{15}}{5}$

・・・エオカキ

次に，チェバの定理より

$\cfrac{\text{AD}}{\text{DB}}\cdot\cfrac{\text{BQ}}{\text{QC}}\cdot\cfrac{\text{CE}}{\text{EA}}=1$

$\cfrac{1}{3}\cdot\cfrac{\text{BQ}}{\text{QC}}\cdot\cfrac{4}{1}=1$

$\cfrac{\text{BQ}}{\text{CQ}}=\cfrac{3}{4}$

・・・クケ

よって，BQ：CQ ＝ 3：4

BC ＝ 7 だから

BQ ＝ 3

・・・コ

ここで上の図に戻ると，内心 I から BC に引いた垂線の接点と B との長さは $4-x=4-1=3$ であり，Q と一致することが分かる。

よって，IQ は内心円の半径だから

IQ ＝ $\cfrac{\sqrt{6}}{2}$

・・・サシ

また，接弦定理より

∠AED ＝ ∠EFD

余弦定理より

$1^2=\Big(\cfrac{2\sqrt{15}}{5}\Big)^2+1^2-2\cdot\cfrac{2\sqrt{15}}{5}\cdot1\cdot\cos$∠AED

$1=\cfrac{12}{5}+1-\cfrac{4\sqrt{15}}{5}\cos$∠AED

$\cfrac{4\sqrt{15}}{5}\cos$∠AED $=\cfrac{12}{5}$

$\cos$∠AED ＝ $\cfrac{3}{\sqrt{15}}=\cfrac{\sqrt{15}}{5}$

したがって $\cos$∠DEF ＝ $\cfrac{\sqrt{15}}{5}$

・・・スセソ

第5問　問題文

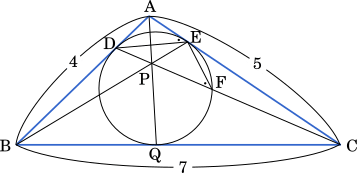
△ABC において, AB＝4, BC＝7, AC＝5 とする。

このとき, $\cos$∠BAC＝$-\cfrac{1}{5}$, $\sin$∠BAC＝$\cfrac{2\sqrt{6}}{5}$ である。

△ABC の内接円の半径は $\cfrac{\sqrt{\boxed{\text{ア}}}}{\boxed{\text{イ}}}$ である。

この内接円と辺 AB との接点をD, 辺 AC との接点を E とする。

AD＝$\boxed{\text{ウ}}$，DE＝$\cfrac{\boxed{\text{エ}}\sqrt{\boxed{\text{オカ}}}}{\boxed{\text{キ}}}$ である。

線分 BE と線分 CD の交点を P, 直線 AP と辺 BC の交点を Q とする。

$\cfrac{\text{BQ}}{\text{CQ}}=\cfrac{\boxed{\text{ク}}}{\boxed{\text{ケ}}}$

であるから, BQ＝$\boxed{\text{コ}}$ であり, △ABC の内心を I とすると

IQ＝$\cfrac{\sqrt{\boxed{\text{サ}}}}{\boxed{\text{シ}}}$

である。また, 直線 CP と △ABC の内接円との交点で D とは異なる点を F とすると

$\cos$∠DFE＝$\cfrac{\sqrt{\boxed{\text{スセ}}}}{\boxed{\text{ソ}}}$

である。