【スマホで読む・わかりやすい】センター数学IA2019本試【解説・正解・問題】

第2問　解答・解説

アイ ウ, エ －1 4, 2　オカ キ 15 4

ク ケ 1 4　コ 4　サ シス セ 7 15 4

ソ 3　タ 4

チ,ツ 4,7 (解答の順序は問わない)

テ 0　ト 0　ナ 1　ニ 2

〔1〕

余弦定理より

$4^2=3^2+2^2-2\cdot3\cdot2\cos$∠BAC

$16=9+4-12\cos$∠BAC

$12\cos$∠BAC＝－3

$\cos$∠BAC＝$\cfrac{-1}{4}$

・・・アイウ

したがって，∠BAC は 90°以上の角だから鈍角である。

・・・エ

また，$\sin^2x+\cos^2x=1$ より

$\sin^2$∠BAC＋$\Big(-\cfrac{1}{4}\Big)^2=1$

$\sin^2$∠BAC＝$\cfrac{15}{16}$

$\sin$∠BAC＝$\cfrac{\sqrt{15}}{4}$

・・・オカキ

∠CAD＝180°－∠BAC だから

$\cos$∠CAD＝$-\cos$∠BAC＝$\cfrac{1}{4}$

・・・クケ

AD を求めると

点 A から AC の中点までの長さは 1 だから

AD $\cos$∠CAD＝1

AD・$\cfrac{1}{4}$＝1

AD ＝ 4

・・・コ

△DBC の面積は公式 $S=\cfrac{1}{2}bc\sin A$ より

$S=\cfrac{1}{2}$ BD・BC $\sin$ ∠ABC

ここで，正弦定理より

$\cfrac{4}{\sin\angle\text{BAC}}=\cfrac{2}{\sin\angle\text{ABC}}$

$2\sin$∠ABC＝$\sin$∠BAC＝$\cfrac{\sqrt{15}}{4}$

$\sin$∠ABC＝$\cfrac{\sqrt{15}}{8}$

よって

$S=\cfrac{1}{2}(3+4)\cdot4\cdot\cfrac{\sqrt{15}}{8}$

$=\cfrac{7\sqrt{15}}{4}$

・・・サシスセ

〔2〕

(1)

図1を見ると，2013年は最小値が 70 以上 75 未満だから，ヒストグラムは③

・・・ソ

また，2017年は最大値が 120 以上 125 未満だから，ヒストグラムは④

・・・タ

(2)

④ 図3よりモンシロチョウの初見日の四分位範囲は 15 日以上である。よって，誤り。

⑦ 切片が 15 の直線より左上にあるデータはそれぞれの初見日の差が 15 日以上である。よって，当てはまるデータが 1 つあるので，誤り。

・・・チツ

(3)

$X$ の偏差の平均値を求めると

$\cfrac{1}{n}(x_1-\overline{x}+\cdots+x_n-\overline{x})$

$=\cfrac{1}{n}(x_1+\cdots+x_n)-\cfrac{1}{n}n\overline{x}$

$=\overline{x}-\overline{x}=0$

・・・テ

$X’$ の平均値と求めると

$\overline{x’}=\cfrac{1}{n}(x_1’+\cdots+x_n’)$

$=\cfrac{1}{n}\Big(\cfrac{x_1-\overline{x}}{s}+\cdots+\cfrac{x_n-\overline{x}}{s}\Big)$

$=\cfrac{1}{s}\cdot\cfrac{1}{n}(x_1-\overline{x}+\cdots+x_n-\overline{x})$

(i) より $\cfrac{1}{n}(x_1-\overline{x}+\cdots+x_n-\overline{x})=0$ だから

$\overline{x’}=0$

・・・ト

(iii) $X’$ の分散を求めると

$s’^2=\cfrac{1}{n}(x_1’^2+\cdots+x_n’^2)$

$=\cfrac{1}{n}\Big\{\Big(\cfrac{x_1-\overline{x}}{s}\Big)^2+\cdots+\Big(\cfrac{x_n-\overline{x}}{s}\Big)^2\Big\}$

$=\cfrac{1}{s^2}\cdot\cfrac{1}{n}\{(x_1-\overline{x})^2+\cdots+(x_n-\overline{x})^2\}$

$=\cfrac{1}{s^2}\cdot s^2=1$

よって，分散が 1 だから $X’$ の標準偏差は 1

・・・ナ

また，$M’$ と $T’$ の散布図を考えると

$x_i’=\cfrac{x_i-\overline{x}}{s}=\cfrac{1}{s}x_i-\cfrac{\overline{x}}{s}$

ここで，$\overline{x}$ と $s$ は定数だから，$x_i’$ と $x_i$ は比例の関係であり，$M’$ と $T’$ の散布図の縦と横の位置関係はもとの散布図と同じである。よって，選択肢⓪と②に絞って検討する。

選択肢⓪のデータは －1 から 1 の間にあるので，偏差は －1 以上 1 以下である。よって，偏差の 2 乗は 1 より小さい値になる。また，分散は偏差の 2 乗の平均だから，その値は 1 より小さい値になる。よって，標準偏差は 1 より小さい値になるので，不適。

選択肢②のデータは －2 から 2 の間にあるので，偏差は －2 以上 2 以下である。よって，偏差の 2 乗は 4 より小さい値になる。また，分散は 0 以上 4 以下の値となるので，標準偏差は 1 になり得る。よって，②が正しい。

・・・ニ

第2問　問題文

〔1〕△ABCにおいて, AB＝3, BC＝4, AC＝2 とする。

次の $\boxed{\text{エ}}$ には, 下の⓪~②のうちから当てはまるものを一つ選べ。

$\cos$∠BAC＝$\cfrac{\boxed{\text{アイ}}}{\boxed{\text{ウ}}}$ であり, ∠BACは $\boxed{\text{エ}}$ である。また, $\sin$∠BAC＝$\frac{\sqrt{\boxed{\text{オカ}}}}{\boxed{\text{キ}}}$ である。

⓪ 鋭角　① 直角　② 鈍角

線分 AC の垂直二等分線と直線 AB の交点を D とする。

$\cos$∠CAD＝$\cfrac{\boxed{\text{ク}}}{\boxed{\text{ケ}}}$ であるから, AD＝$\boxed{\text{コ}}$ であり, △DBC の面積は $\cfrac{\boxed{\text{サ}}\sqrt{\boxed{\text{シス}}}}{\boxed{\text{セ}}}$ である。

〔2〕全国各地の気象台が観測した「ソメイヨシノ(桜の種類)の開花日」や, 「モンシロチョウの初見日(初めて観測した日)」, 「ツバメの初見日」などの日付を気象庁が発表している。気象庁発表の日付は普通の月日形式であるが, この問題では該当する年の 1 月 1 日を「1」とし, 12 月 31 日を「365」(うるう年の場合は「366」)とする「年間通し日」に変更している。例えば, 2 月 3 日は,
1 月 31 日の「31」に 2 月 3 日の 3 を加えた「34」となる。

(1) 図 1 は全国 48 地点で観測しているソメイヨシノの 2012 年から 2017 年までの 6 年間の開花日を, 年ごとに箱ひげ図にして並べたものである。

図 2 はソメイヨシノの開花日の年ごとのヒストグラムである。ただし, 順番は年の順に並んでいるとは限らない。なお, ヒストグラムの各階級の区間は, 左側の数値を含み, 右側の数値を含まない。

次の $\boxed{\text{ソ}}$, $\boxed{\text{タ}}$ に当てはまるものを, 図 2 の ⓪~⑤のうちから一つずつ選べ。

・2013 年のヒストグラムは $\boxed{\text{ソ}}$ である。

・2017 年のヒストグラムは $\boxed{\text{タ}}$ である。

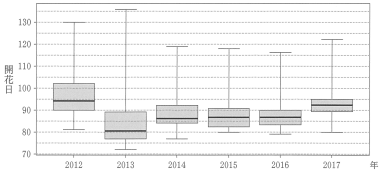
図1 ソメイヨシノの開花日の年別の箱ひげ図

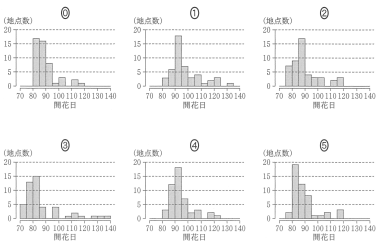
図2 ソメイヨシノの開花日の年別のヒストグラム

(出典：図1, 図2は気象庁「生物季節観測データ」Web ページにより作成)

(2) 図 3 と 図 4 は, モンシロチョウとツバメの両方を観測している 41 地点における, 2017 年の初見日の箱ひげ図と散布図である。散布図の点には重なった点が 2 点ある。なお, 散布図には原点を通り傾き 1 の直線(実線), 切片が －15 および 15 で傾きが 1 の 2 本の直線(破線) を付加している。

次の $\boxed{\text{チ}}$, $\boxed{\text{ツ}}$ に当てはまるものを, 下の⓪~⑦のうちから一つずつ選べ。ただし, 解答の順序は問わない。

図 3, 図 4 から読み取れることとして正しくないものは, $\boxed{\text{チ}}$, $\boxed{\text{ツ}}$ である。

⓪ モンシロチョウの初見日の最小値はツバメの初見日の最小値と同じである。

① モンシロチョウの初見日の最大値はツバメの初見日の最大値より大きい。

② モンシロチョウの初見日の中央値はツバメの初見日の中央値より大きい。

③ モンシロチョウの初見日の四分位範囲はツバメの初見日の四分位範囲の 3 倍より小さい。

④ モンシロチョウの初見日の四分位範囲は 15 日以下である。

⑤ ツバメの初見日の四分位範囲は 15 日以下である。

⑥ モンシロチョウとツバメの初見日が同じ所が少なくとも 4 地点ある。

⑦ 同一地点でのモンシロチョウの初見日とツバメの初見日の差は 15 日以下である。

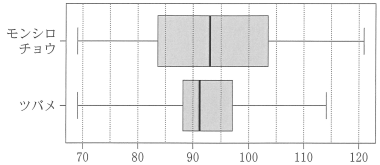
図3 モンシロチョウとツバメの初見日(2017 年)の箱ひげ図

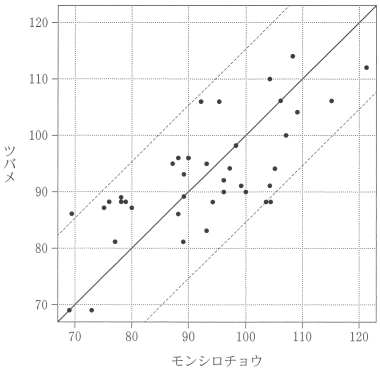
図4 モンシロチョウとツバメの初見日(2017 年)の散布図

(出典：図3, 図4は気象庁「生物季節観測データ」Web ページにより作成)

(3) 一般に $n$ 個の数値 $x_1$, $x_2$, $\dots$, $x_n$ からなるデータ $X$ の平均値を $\overline{x}$, 分散を $s^2$, 標準偏差を $s$ とする。各 $x_i$ に対して

$x’_i=\cfrac{x_i-\overline{x}}{s}$ $(i=1, 2, \cdots, n)$

と変換した $x’_1$, $x’_2$, $\cdots$, $x’_n$ をデータ $X’$ とする。ただし, $n$ ≧ 2, $s$ ＞ 0 とする。

次の $\boxed{\text{テ}}$,$\boxed{\text{ト}}$, $\boxed{\text{ナ}}$ に当てはまるものを, 下の⓪~⑧の
うちから一つずつ選べ。ただし, 同じものを繰り返し選んでもよい。

・$X$ の偏差 $x_1-\overline{x}$, $x_2-\overline{x}$, $\cdots$, $x_n-\overline{x}$ の平均値は $\boxed{\text{テ}}$ である。

・$X’$ の平均値は $\boxed{\text{ト}}$ である。

・$X’$ の標準偏差は $\boxed{\text{ナ}}$ である。

⓪ 0　① 1　② －1

③ $\overline{x}$　④ $s$　⑤ $\cfrac{1}{s}$

⑥ $s^2$　⑦ $\cfrac{1}{s^2}$　⑧ $\cfrac{\overline{x}}{s}$

図 4 で示されたモンシロチョウの初見日のデータ $M$ とツバメの初見日のデータ $T$ について上の変換を行ったデータをそれぞれ $M’$, $T’$ とする。

次の $\boxed{\text{ニ}}$ に当てはまるものを, 図 5 の⓪~③のうちから一つ選べ。

変換後のモンシロチョウの初見日のデータ $M’$ と変換後のツバメの初見日のデータ $T’$ の散布図は, $M$ と $T$ の標準偏差の値を考慮すると $\boxed{\text{ニ}}$ である。

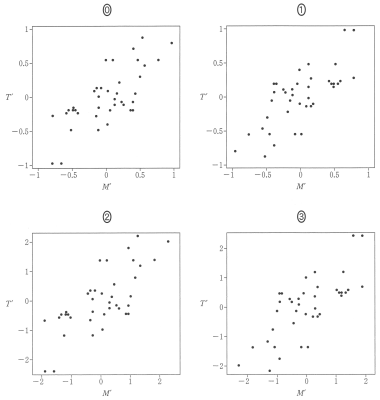
図5 四つの散布図