【スマホで読む・わかりやすい】センター数学IA2018追試【解説・正解・問題】

第5問　解答・解説

アイ ウ 10 1　エ オカ キ 2 10 5

ク 2　ケコ 24　サシ 60　スセソ 120

タチ 32　ツ 5

〔1〕

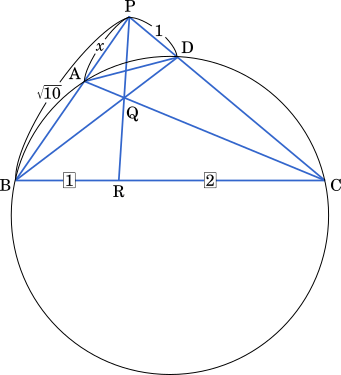
方べきの定理より

PA・PB＝PD・PC

$x\cdot\sqrt{10}=1\cdot$PC

$\sqrt{10}x$＝CD＋1

CD＝$\sqrt{10}x-1$

・・・アイウ

また

$\cfrac{\text{RC}}{\text{BR}}=2=\cfrac{2}{1}$

よって，RC：BR＝2：1

チェバの定理より

$\cfrac{\text{PA}}{\text{AB}}\cdot\cfrac{\text{BR}}{\text{RC}}\cdot\cfrac{\text{CD}}{\text{DP}}=1$

$\cfrac{x}{\sqrt{10}-x}\cdot\cfrac{1}{2}\cdot\cfrac{\sqrt{10}x-1}{1}=1$

$\cfrac{x(\sqrt{10}x-1)}{2(\sqrt{10}-x)}=1$

$x(\sqrt{10}x-1)=2(\sqrt{10}-x)$

$\sqrt{10}x^2-x=2\sqrt{10}-2x$

$\sqrt{10}x^2+x-2\sqrt{10}=0$

$x=\cfrac{-1\pm\sqrt{1+80}}{2\sqrt{10}}$

$\cfrac{-1\pm9}{2\sqrt{10}}=\cfrac{-10}{2\sqrt{10}},\cfrac{8}{2\sqrt{10}}$

$=-\cfrac{5}{\sqrt{10}},\cfrac{4}{\sqrt{10}}$

$=-\cfrac{\sqrt{10}}{2},\cfrac{2\sqrt{10}}{5}$

$x$ ＞ 0 より

$x=\cfrac{2\sqrt{10}}{5}$

・・・エオカキ

〔2〕

立方体では $v=8$，$e=12$，$f=6$ だから

$v-e+f=8-12+6=2$

・・・ク

$v$：$e$＝2：5 かつ $f=38$ のとき

$2e=5v$

$e=\cfrac{5}{2}v$

$v-e+f=2$ に代入して

$v-\cfrac{5}{2}v+38=2$

$v=24$

・・・ケコ

よって

$e=\cfrac{5}{2}\cdot24=60$

・・・サシ

これより，頂点の数 $v=24$，辺の数 $e=60$，面の数 $f=38$ となることから

$x+y=38$

$y=38-x$

正三角形の辺の数は $3x$，正方形の辺の数は $4x$ で表される。各面はそれぞれとなり合う面と各辺を共有するので，多面体の辺の数はそれぞれの辺の数の合計を 2 で割ったものである。

$\cfrac{3x+4y}{2}=60$

$3x+4y=120$

・・・スセソ

$y=38-x$ を代入すると

$3x+4(38-x)=120$

$3x+152-4x=120$

$x=32$

・・・タチ

また，各頂点はとなり合う頂点と辺を共有する。頂点の数は 24 個だから

$\cfrac{24\ell}{2}=60$

$\ell=5$

・・・ツ

第５問　問題文

〔1〕円に内接する四角形 ABCD の辺 AB の端点 A の側の延長と辺 CD の端点 D の側の延長が点 P で交わるとする。さらに，PA ＝ $x$，PB ＝ $\sqrt{10}$ および PD ＝ 1 とする。このとき

CD ＝ $\sqrt{\boxed{\text{アイ}}}x-\boxed{\text{ウ}}$

である。

対角線 AC と BD の交点を Q，直線 PQ と辺 BC の交点を R とし

$\cfrac{\text{RC}}{\text{BR}}=2$

とする。このとき

$x$ ＝ $\cfrac{\boxed{\text{エ}}\sqrt{\boxed{\text{オカ}}}}{\boxed{\text{キ}}}$

である。

〔2〕一般の凸多面体（へこみのない多面体）の頂点の数 $v$，辺の数 $e$，面の数 $f$ について $v-e+f$ の値を考える。例えば，立方体の場合で考えると，この値は $\boxed{\text{ク}}$ である。

以下では $v$：$e$ ＝2：5 かつ $f$ ＝ 38 であるような凸多面体について考える。オイラーの多面体定理により $v-e+f$ ＝ $\boxed{\text{ク}}$ であることがわかるので，$v$ ＝ $\boxed{\text{ケコ}}$，$e$ ＝ $\boxed{\text{サシ}}$ である。

さらに，この凸多面体は $x$ 個の正三角形の面と $y$ 個の正方形の面で構成されていて，各頂点に集まる辺の数はすべて同じ $\ell$ であるとする。このとき $3x+4y=\boxed{\text{スセソ}}$ であることから $x$ ＝ $\boxed{\text{タチ}}$ であり，さらに $\ell$ ＝ $\boxed{\text{ツ}}$ である。