【スマホで読む・わかりやすい】センター数学IA2018本試【解説・正解・問題】

第2問　解答・解説

ア イ 7 9　ウ エ オ 4 2 9　カ,キ 0,4

ク ケコ 2 33

サ,シ 1,6 (解答の順序は問わない)

ス,セ 4,5 (解答の順序は問わない)

ソ 2

〔1〕

余弦定理より

$6^2=5^2+9^2-2\cdot5\cdot9\cos$∠ABC

$36=25+81-90\cos$∠ABC

$90\cos$∠ABC＝70

$\cos$∠ABC＝$\cfrac{7}{9}$

・・・アイ

$\sin^2x+\cos^2x=1$ より

$\sin^2$∠ABC＋$\Big(\cfrac{7}{9}\Big)^2=1$

$\sin^2$∠ABC＝$\cfrac{32}{81}$

$\sin$∠ABC＝$\cfrac{4\sqrt{2}}{9}$

・・・ウエオ

四角形 ABCD が台形のとき

AB・$\sin$∠ABC＝$5\cdot\cfrac{4\sqrt{2}}{9}=\cfrac{20\sqrt{2}}{9}$

CD＝3 だから，値を比べると

$20\sqrt{2}=\sqrt{800}$

$\sqrt{784}$ ＜ $\sqrt{800}$ ＜ $\sqrt{841}$

28 ＜ $\sqrt{800}$ ＜ 29

$\cfrac{27}{9}$ ＜ $\cfrac{28}{9}$ ＜ $\cfrac{20\sqrt{2}}{9}$ ＜ $\cfrac{29}{4}$ ＜ $\cfrac{36}{9}$

3 ＜ $\cfrac{20\sqrt{2}}{9}$ ＜ 4

したがって

CD ＜ AB・$\sin$∠ABC

・・・カ

AB・$\sin$∠ABC は，A から BC に下ろした垂線の長さである。もし，AD // BC として台形を描くと，垂線の長さは CD と同じ，または短くなる。これは上の不等式と矛盾するので，四角形 ABCD は AB // CD の台形である。

・・・キ

AC と BD の交点を E とすると，余弦定理より

$9^2=5^2+6^2-2\cdot5\cdot6\cos$∠CAB

$81=25+36-60\cos$∠CAB

$60\cos$∠CAB＝－20

$\cos$∠CAB＝$-\cfrac{1}{3}$

△ABE∽△CDE だから

AC＝6，AE：CE＝5：3 より

AE＝$6\cdot\cfrac{5}{8}=\cfrac{15}{4}$

∠CAB＝∠EAB だから，余弦定理より

$\text{EB}^2=5^2+\Big(\cfrac{15}{4}\Big)^2-2\cdot5\cdot\cfrac{15}{4}\cos$∠EAB

$=25+\cfrac{225}{16}-\cfrac{75}{2}\Big(-\cfrac{1}{3}\Big)$

$=25+\cfrac{225}{16}+\cfrac{25}{2}$

$=\cfrac{400+225+200}{16}=\cfrac{825}{16}$

EB＝$\cfrac{5\sqrt{33}}{4}$

BE：DE＝5：3 だから

BD＝$\cfrac{5\sqrt{33}}{4}\cdot\cfrac{8}{5}=2\sqrt{33}$

・・・クケコ

〔2〕

(1)

⓪ 範囲が最も大きいのは，男子短距離グループだから，誤り。

① 正しい。

② 男子長距離グループの中央値は 176cm だが，度数最大の階級は 170cm 以上 175cm 未満だから，誤り。

③ 第1四分位数は 160cm 以上 162cm 未満だから，誤り。

④ すべての選手の中で最も身長の高い選手は男子短距離グループの中にいるので，誤り。

⑤ すべての選手の中で最も身長の低い選手は女子短距離グループの中にいるので，誤り。

⑥　正しい。

・・・サシ

(2)

$Z=\cfrac{W}{X}$ より，$X$ に対して $W$ の値が小さくなるほど $Z$ は小さくなることが分かる。これは，言い換えればデータが右下方向にあるほど $Z$ は小さくなるということである。

これをもとに $Z$ の箱ひげ図を見ると，女子長距離が(d)，男子短距離が(a)であることは容易に分かる。また，男子長距離と女子短距離について考えると，直線 $l_3$ と $l_4$ の間にあるデータのうち，最も $l_4$ に近いデータは男子長距離のなかにある。このデータは $Z$ の最大値を表すので，男子長距離が(c)，女子短距離が(b)である。

⓪ すべてのグループにおいて，$X$ と $W$ には正の相関があるので，誤り。

① 中央値が最も大きいのは男子短距離グループだから，誤り。

② $Z$ の範囲が最小なのは女子長距離グループだから，誤り。

③ 男子短距離距離グループは四分位範囲が最も大きいので，誤り。

④ 正しい。

⑤ 正しい。

・・・スセ

(3)

式を展開すると

$(x_1-\overline{x})(w_1-\overline{w})+\cdots+(x_n-\overline{x})(w_n-\overline{w})$

$=x_1w_1-x_1\overline{w}-w_1\overline{x}+\overline{x}\overline{w}+\cdots+x_nw_n-x_n\overline{w}-w_n\overline{x}+\overline{x}\overline{w}$

$=(x_1w_1+\cdots+x_nw_n)-(x_1+\cdots+x_n)\overline{w}-(w_1+\cdots+w_n)\overline{x}+n\overline{x}\overline{w}$

ここで，$x_1+\cdots+x_n=n\overline{x}$，$w_1+\cdots+w_n=n\overline{w}$ だから

$=x_1w_1+\cdots+x_nw_n-n\overline{x}\overline{w}-n\overline{x}\overline{w}+n\overline{x}\overline{w}$

$=x_1w_1+\cdots+x_nw_n-n\overline{x}\overline{w}$

・・・ソ

第２問

〔1〕四角形 ABCD において，3 辺の長さをそれぞれ AB ＝ 5，BC ＝ 9，CD ＝ 3，対角線 AC の長さを AC ＝ 6 とする。このとき

$\cos$∠ABC＝$\cfrac{\boxed{\text{ア}}}{\boxed{\text{イ}}}$，$\sin$∠ABC＝$\cfrac{\boxed{\text{ウ}}\sqrt{\boxed{\text{エ}}}}{\boxed{\text{オ}}}$

である。

ここで，四角形 ABCD は台形であるとする。

次の $\boxed{\text{カ}}$ には下の⓪～②から，$\boxed{\text{キ}}$ には③・④から当てはまるものを一つずつ選べ。

CD $\boxed{\text{カ}}$ AB・$\sin$ ∠ABC であるから $\boxed{\text{キ}}$ である。

⓪ ＜　① ＝　② ＞

③ 辺 AD と辺 BC が平行

④ 辺 AB と辺 CD が平行

したがって

BD ＝ $\boxed{\text{ク}}\sqrt{\boxed{\text{ケコ}}}$

である。

〔2〕ある陸上競技大会に出場した選手の身長（単位はcm）と体重（単位はkg）のデータが得られた。男子短距離，男子長距離，女子短距離，女子長距離の四つのグループに分けると，それぞれのグループの選手数は，男子短距離が 328 人，男子長距離が 271 人，女子短距離が 319 人，女子長距離が 263 人である。

(1) 次ページの図1および図2は，男子短距離，男子長距離，女子短距離，女子長距離の四つのグループにおける，身長のヒストグラムおよび箱ひげ図である。

次の $\boxed{\text{サ}}$，$\boxed{\text{シ}}$ に当てはまるものを，下の⓪～⑥のうちから一つずつ選べ。ただし，解答の順序は問わない。

図1および図2から読み取れる内容として正しいものは， $\boxed{\text{サ}}$，$\boxed{\text{シ}}$ である。

⓪ 四つのグループのうちで範囲が最も大きいのは，女子短距離グループである。

① 四つのグループのすべてにおいて，四分位範囲は 12 未満である。

② 男子長距離グループのヒストグラムでは，度数最大の階級に中央値が入っている。

③ 女子長距離グループのヒストグラムでは，度数最大の階級に第1四分位数が入っている。

④ すべての選手の中で最も身長の高い選手は，男子長距離グループの中にいる。

⑤ すべての選手の中で最も身長の低い選手は，女子長距離グループの中にいる。

⑥ 男子短距離グループの中央値と男子長距離グループの第3四分位数は，ともに 180 以上 182 未満である。

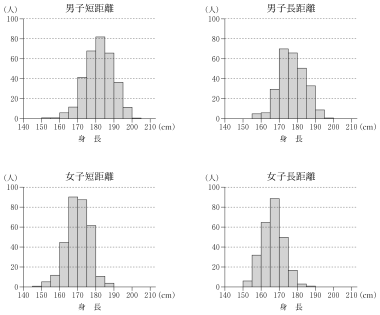
図1 身長のヒストグラム

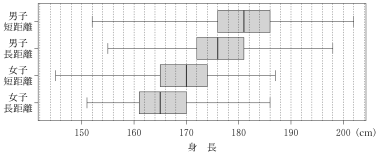
図2 身長の箱ひげ図

（出典：図1，図2はガーディアン社の Web ページにより作成）

(2) 身長を $H$，体重を $W$ とし，$X$ を $X$＝$\Big(\cfrac{H}{100}\Big)^2$ で，$Z$ を $Z$＝$\cfrac{W}{X}$ で定義する。次ページの図3は，男子短距離，男子長距離，女子短距離，女子長距離の四つのグループにおける $X$ と $W$ のデータの散布図である。ただし，原点を通り，傾きが 15，20，25，30 である四つの直線 $l_1$，$l_2$，$l_3$，$l_4$ も補助的に描いている。また，次ページの図4の(a)，(b)，(c)，(d)で示す $Z$ の四つの箱ひげ図は，男子短距離，男子長距離，女子短距離，女子長距離
の四つのグループのいずれかの箱ひげ図に対応している。

次の $\boxed{\text{ス}}$，$\boxed{\text{セ}}$ に当てはまるものを，下の⓪～⑤のうちから一つずつ選べ。ただし，解答の順序は問わない。

図3および図4から読み取れる内容として正しいものは，$\boxed{\text{ス}}$，$\boxed{\text{セ}}$ である。

⓪ 四つのグループのすべてにおいて，$X$ と $W$ には負の相関がある。

① 四つのグループのうちで $Z$ の中央値が一番大きいのは，男子長距離グループである。

② 四つのグループのうちで $Z$ の範囲が最小なのは，男子長距離グループである。

③ 四つのグループのうちで $Z$ の四分位範囲が最小なのは，男子短距離グループである。

④ 女子長距離グループのすべての $Z$ の値は 25 より小さい。

⑤ 男子長距離グループの $Z$ の箱ひげ図は(c)である。

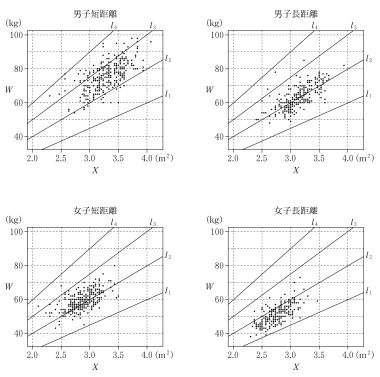
図3 $X$ と $W$ の散布図

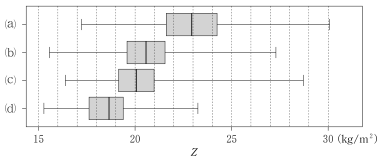
図4 $Z$ の箱ひげ図

（出典：図3，図4はガーディアン社の Web ページにより作成）

(3) $n$ を自然数とする。実数値のデータ $x_1$，$x_2$，$\cdots$，$x_n$ および $w_1$，$w_2$，$\cdots$，$w_n$ に対して，それぞれの平均値を

$\overline{x}$＝$\cfrac{x_1+x_2+\cdots+x_n}{n}$，

$\overline{w}$＝$\cfrac{w_1+w_2+\cdots+w_n}{n}$

とおく。等式$(x_1$＋$x_2$＋$\cdots$＋$x_n)\overline{w}$＝$n\overline{xw}$ などに注意すると，偏差の積の和は

$(x_1-\overline{x})(w_1-\overline{w})+(x_2-\overline{x})(w_2-\overline{w})+\cdots+(x_n-\overline{x})(w_n-\overline{w})$＝$x_1w_1+x_2w_2+\cdots+x_nw_n-\boxed{\text{ソ}}$

となることがわかる。$\boxed{\text{ソ}}$ に当てはまるものを，次の⓪～③のうちから一つ選べ。

⓪ $\overline{xw}$　① $(\overline{x}\space\overline{w})^2$　② $n\space\overline{x}\space\overline{w}$　③ $n^2\overline{x}\space\overline{w}$