【スマホで読む・わかりやすい】センター数学IA2017追試【解説・正解・問題】

第5問　解答・解説

ア イ 2 3　ウ エ 2 3　オカ キ 18 5

ク ケ 1 2　コ サ 4 5　シ 2

スセ ソ 32 5　タ チツ 9 32

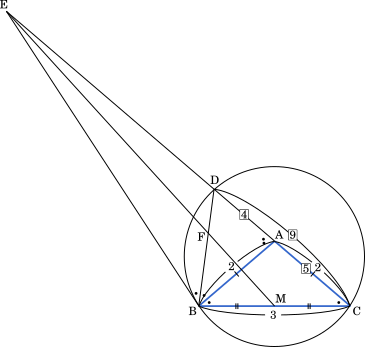
角二等分線の性質を用いて

BC：BD＝AC：AD

3：BD＝2：AD

3AD＝2BD

$\cfrac{\text{AD}}{\text{BD}}=\cfrac{2}{3}$

・・・アイ

△ABD ∽ △BCD より

BD：CD＝AB：BC

BD：CD＝2：3

3BD＝2CD

$\cfrac{\text{BD}}{\text{CD}}=\cfrac{2}{3}$

・・・ウエ

また

$\cfrac{\text{AD}}{\text{CD}}=\cfrac{\text{AD}}{\text{BD}}\cdot\cfrac{\text{BD}}{\text{CD}}$

$=\cfrac{2}{3}\cdot\cfrac{2}{3}=\cfrac{4}{9}$

よって，AD：CD＝4：9 となり，AC：AD＝5：4 である。これを用いて

CD＝$2\cdot\cfrac{9}{5}=\cfrac{18}{5}$

・・・オカキ

また，△BCD の外接円をつくると，接弦定理より

∠DBE＝∠DCB＝∠ABD

したがって

∠DBE＝$\cfrac{1}{2}$∠ABE

・・・クケ

さらに角二等分線の性質より

BA：BE＝AD：DE

ここで

AD＝AC・$\cfrac{4}{5}=2\cdot\cfrac{4}{5}=\cfrac{8}{5}$

よって

2：BE＝$\cfrac{8}{5}$：DE

2DE＝$\cfrac{8}{5}$ BE

$\cfrac{\text{DE}}{\text{BE}}=\cfrac{4}{5}$

・・・コサ

次に，BE と同じ長さの線分を求めると

三角形の外角の性質より

∠EAB＝∠ABC＋∠ACB

よって，∠BAE＝∠ABE となるので，△EAB は BE＝AE の二等辺三角形。

・・・シ

また，DE の長さを求めると

DE＝AE－AD

BE＝AE，AD＝$\cfrac{8}{5}$ より

DE=BE－$\cfrac{8}{5}$

DE：BE＝4：5 より

BE＝$\cfrac{5}{4}$ DE

これを代入して

DE＝$\cfrac{5}{4}$ DE－$\cfrac{8}{5}$

$\cfrac{1}{4}$ DE＝$\cfrac{8}{5}$

DE＝$\cfrac{32}{5}$

・・・スセソ

さらに，メネラウスの定理より

$\cfrac{\text{ED}}{\text{DC}}\cdot\cfrac{\text{CB}}{\text{BM}}\cdot\cfrac{\text{MF}}{\text{FE}}=1$

$\cfrac{\space\cfrac{32}{5}\space}{\cfrac{18}{5}}\cdot\cfrac{2}{1}\cdot\cfrac{\text{FM}}{\text{EF}}=1$

ここで

$\cfrac{\cfrac{32}{5}}{\cfrac{18}{5}}=\cfrac{\cfrac{32}{5}\times5}{\cfrac{18}{5}\times5}=\cfrac{32}{18}=\cfrac{16}{9}$

よって

$\cfrac{16}{9}\cdot\cfrac{2}{1}\cdot\cfrac{\text{FM}}{\text{EF}}=1$

$\cfrac{\text{FM}}{\text{EF}}=\cfrac{9}{32}$

・・・タチツ

第5問　問題文

二等辺三角形 ABC において, AB = AC = 2, BC = 3 とする。

直線 AC 上に, C とは異なる点 D を ∠ABC = ∠ABD を満たすようにとると，$\cfrac{\text{AD}}{\text{DB}}=\cfrac{\boxed{\text{ア}}}{\boxed{\text{イ}}}$ である。△ABD と △BCD において, ∠ABD = ∠BCD で ∠D は共通であるから, $\cfrac{\text{BD}}{\text{CD}}=\cfrac{\boxed{\text{ウ}}}{\boxed{\text{エ}}}$ である。$\cfrac{\text{AD}}{\text{CD}}=\cfrac{\text{AD}}{\text{BD}}\cdot\cfrac{\text{BD}}{\text{CD}}$ に着目すると, CD = $\cfrac{\boxed{\text{オカ}}}{\boxed{\text{キ}}}$ である。

△BCD の外接円を O とし, 点 B における円 O の接線と直線 AC との交点を E とすると, 点 E は辺 AC の A の側の延長上にある。このとき

∠DBE = $\cfrac{\boxed{\text{ク}}}{\boxed{\text{ケ}}}$ ∠ABE

であるから, $\cfrac{\text{DE}}{\text{BE}}=\cfrac{\boxed{\text{コ}}}{\boxed{\text{サ}}}$ である。

また, 線分 BE は線分 $\boxed{\text{シ}}$ と同じ長さである。$\boxed{\text{シ}}$ に当てはまるものを, 次の ⓪~④のうちから一つ選べ。

⓪ AB　① AD　② AE　③ BC　④ CD

したがって, DE = $\cfrac{\boxed{\text{スセ}}}{\boxed{\text{ソ}}}$ である。

辺 BC の中点を M とし, 線分 EM と線分 BD の交点を F とすると

$\cfrac{\text{FM}}{\text{EF}}=\cfrac{\boxed{\text{タ}}}{\boxed{\text{チツ}}}$

である。