【スマホで読む・わかりやすい】センター数学IA2017追試【解説・正解・問題】

第2問　解答・解説

ア 3　イ 7　ウ エ 1 2　オカ キ 21 3

クケ コ －1 2　サ シ 1 2　ス 3

セ,ソ 1, 4 (解答の順序は問わない)

タ 1　チ 3　ツ 4

〔1〕

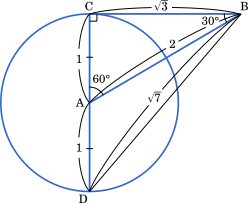
∠ACB ＝ 90° より，△ABC は辺の比が 1：2：$\sqrt{3}$ の直角二等辺三角形である。したがって，BC＝$\sqrt{3}$

・・・ア

また，三平方の定理より

BD＝$\sqrt{\text{BC}^2+\text{CD}^2}$

$=\sqrt{(\sqrt{3})^2+2^2}$

$=\sqrt{3+4}=\sqrt{7}$

・・・イ

さらに，∠ABC＝30° だから

$\sin$∠ABC＝$\cfrac{1}{2}$

・・・ウエ

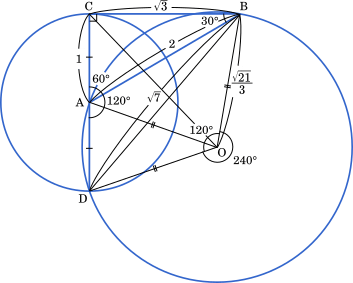
次に △ABD の外接円の半径を求めると

∠BAC＝60° より ∠BAD＝120°

正弦定理より

$2R=\cfrac{\sqrt{7}}{\sin\angle\text{BAD}}$

$=\cfrac{\space\sqrt{7}\space}{\cfrac{\sqrt{3}}{2}}=\cfrac{\space\sqrt{7}\times2\space}{\cfrac{\sqrt{3}}{2}\times2}=\cfrac{2\sqrt{7}}{\sqrt{3}}$

$=\cfrac{2\sqrt{21}}{3}$

$R=\cfrac{\sqrt{21}}{3}$

・・・オカキ

円周角と中心角の関係を用いて，∠BOD の点 A を含まない方の弧から作られる中心角は ∠BOD＝240°，これより A を含む方の弧から作られる中心角は ∠BOD＝120°

したがって，$\cos$∠BOD＝$\cfrac{-1}{2}$

・・・クケコ

また，$\sin$∠AOC と $\sin$∠COD の比を求めると，正弦定理より

$\cfrac{1}{\sin\angle\text{AOC}}=\cfrac{\cfrac{\sqrt{21}}{3}}{\sin\angle\text{ACO}}$

式を変形して

$\sin$∠ACO＝$\cfrac{\sqrt{21}}{3}\sin$∠AOC

また

$\cfrac{2}{\sin\angle\text{COD}}=\cfrac{\cfrac{\sqrt{21}}{3}}{\sin\angle\text{DCO}}$

$\sin$∠DCO＝$\cfrac{\sqrt{21}}{6}\sin$∠COD

∠ACO＝∠DCO だから

$\cfrac{\sqrt{21}}{3}\sin$∠AOC＝$\cfrac{\sqrt{21}}{6}\sin$∠COD

2 $\sin$∠AOC＝$\sin$∠COD

したがって

$\cfrac{\sin\angle\text{AOC}}{\sin\angle\text{COD}}=\cfrac{1}{2}$

・・・サシ

〔2〕

(1)

1 組の人数は 34 人だから，第1四分位数は得点の低い方から数えて 9 番目。表 1 より，第1四分位数は 50 点以上 55 点未満に含まれる。したがって，1 組は b である。

また，2 組の人数は 33 人だから，中央値は得点の低い方から数えて 17 番目。表 1 より，中央値は 65 点以上 70 点未満に含まれる。したがって，2 組は c である。

さらに，3 組の人数は 33 人だから，中央値は得点の低い方から 17 番目。表 1 より，中央値は 60 点以上 65 点未満。また，第1四分位数は得点の低い方から数えて 7 番目と 8 番目を足して 2 で割ったものである。表 1 より，7 番目と 8 番目は 55 点以上 60 点未満に含まれる。したがって，3 組は a である。

・・・ス

(2)

① 相関係数 $r$ は，共分散を $s_{sy}$，$x$，$y$ の標準偏差をそれぞれ $s_x$，$s_y$ とすると，$r=\cfrac{s_{xy}}{s_xs_y}$ と表される。したがって，$r=\cfrac{25.0}{8.4\times5.2}=0.57\cdots$ だから，誤り。

④

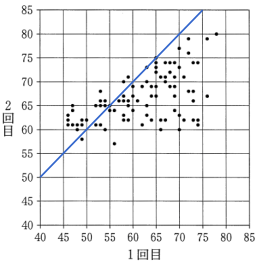
上の図のように直線を引くと，2 回目の得点が 1 回目の得点より 10 点以上高い生徒のデータは，直線より左上にある。この中には 1 回目の得点が 55 点以上の生徒が含まれるので，誤り。

・・・セソ

(3)

1 回目の得点 $x$ を新しい得点に換算したものを $y$ とすると

$y=50+10\times\cfrac{x-61.9}{8.4}$

$=\cfrac{10}{8.4}(x-61.9)+50$

と表すことができる。これは，比例式 $y=\cfrac{10}{8.4}x$ を平行移動したものであるため，もとの得点と新しい得点は比例の関係にある。

同様に 3 回目の得点は

$=\cfrac{10}{26.0}(x-133.3)+50$

となり，比例の関係にある。

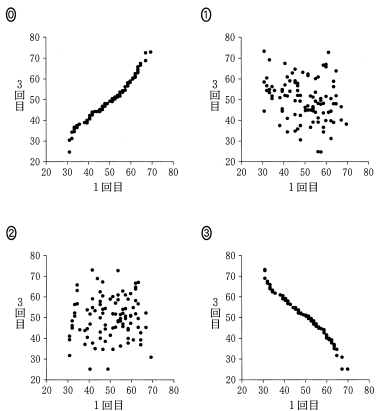
よって，新しい得点で散布図を作ると，データのグラフ上の位置関係は変わらない。したがって，①が正しい。

・・・タ

〔3〕

式を展開すると

$(x_1-\overline{w})^2+(x_2-\overline{w})^2+\cdots+(x_m-\overline{w})^2$

$={x_1}^2-2x_1\overline{w}+(\overline{w})^2+{x_2}^2-2x_2\overline{w}+(\overline{w})^2+\cdots+{x_m}^2-2x_m\overline{w}+(\overline{w})^2$

$=({x_1}^2+{x_2}^2+{x_m}^2)-2\overline{w}(x_1+x_2+\cdots+x_m)+m(\overline{w})^2$

$=m\Big\{\cfrac{1}{m}({x_1}^2+{x_2}^2+{x_m}^2)-(\overline{x})^2\Big\}+m(\overline{x})^2-2\overline{w}(x_1+x_2+\cdots+x_m)+m(\overline{w})^2$

$=m{S_A}^2+m(\overline{x})^2-2\overline{w}(x_1+x_2+\cdots+x_m)+m(\overline{w})^2$

ここで，$x_1+x_2+\cdots+x_m$ は $x$ の合計だから，$m\overline{x}$ と書き換えることができる。

$=m{S_A}^2+m(\overline{x})^2-2m\overline{x}\overline{w}+m(\overline{w})^2$

$=m{S_A}^2+m\{(\overline{x})^2-2\overline{x}\overline{w}+(\overline{w})^2\}$

$=m{S_A}^2+m(\overline{x}-\overline{w})^2$

・・・チ

また，$S^2$ を求めると

$S^2=\cfrac{1}{m+n}\{(x_1-\overline{w})^2+(x_2-\overline{w})^2+\cdots+(x_m-\overline{w})^2+(y_1-\overline{w})^2+(y_2-\overline{w})^2+\cdots+(y_n-\overline{w})^2\}$

ここで，上の計算式を利用すると

$(y_1-\overline{w})^2+(y_2-\overline{w})^2+\cdots+(y_n-\overline{w})^2$

$=n{S_B}^2+n(\overline{y}-\overline{w})^2$

となる。よって

$S^2=\cfrac{1}{m+n}\{m{S_A}^2+m(\overline{x}-\overline{w})^2+n{S_B}^2+n(\overline{y}-\overline{w})^2\}$

式を展開すると

$=\cfrac{1}{m+n}\{m{S_A}^2+m(\overline{x})^2-2m\overline{x}\overline{w}+m(\overline{w})^2+n{S_B}^2+n(\overline{y})^2-2n\overline{y}\overline{w}+n(\overline{w})^2\}$

$=\cfrac{1}{m+n}\{m{S_A}^2+n{S_B}^2+m(\overline{x})^2+n(\overline{y})^2-2\overline{w}(m\overline{x}+n\overline{y})+(m+n)(\overline{w})^2\}$

ここで，$m\overline{x}$，$n\overline{y}$ はそれぞれ $x$，$y$ の合計だから

$\cfrac{m\overline{x}+n\overline{y}}{m+n}=\overline{w}$

$m\overline{x}+n\overline{y}=(m+n)\overline{w}$

と表すことができる。よって

$S^2=\cfrac{1}{m+n}\{m{S_A}^2+n{S_B}^2+m(\overline{x})^2+n(\overline{y})^2-2(m+n)(\overline{w})^2+(m+n)(\overline{w})^2\}$

$=\cfrac{m{S_A}^2+n{S_B}^2+m(\overline{x})^2+n(\overline{y})^2-(m+n)(\overline{w})^2}{m+n}$

・・・ツ

第2問　問題文

〔1〕点 A を中心とする半径 1 の円がある。点 A から距離 2 の位置にある点 B から円 A に接線を 1 本引く。その接線と円 A との接点を C とし, 点 D を線分 CD が円 A の直径となるようにとる。

このとき

BC = $\sqrt{\boxed{\text{ア}}}$, BD = $\sqrt{\boxed{\text{イ}}}$, $\sin$∠ABC = $\cfrac{\boxed{\text{ウ}}}{\boxed{\text{エ}}}$

である。

また，△ABD の外接円の半径は $\cfrac{\sqrt{\boxed{\text{オカ}}}}{\boxed{\text{キ}}}$ である。その外接円の中心を O とすると, $\cos$∠BOD = $\cfrac{\boxed{\text{クケ}}}{\boxed{\text{コ}}}$, $\cfrac{\sin\angle\text{AOC}}{\sin\angle\text{COD}}=\cfrac{\boxed{\text{サ}}}{\boxed{\text{シ}}}$ である。

〔2〕1 組から 3 組の生徒 100 人に対し, テストを 3 回行った。1 回目と 2 回目のテストは 100 点満点, 3 回目は 200 点満点である。

(1) 次の表1および図1は, 1 回目のテストの組ごとの得点に対する度数分布表および箱ひげ図である。

表1

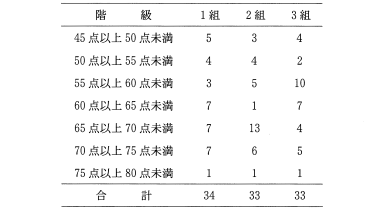
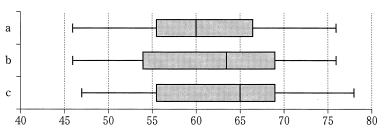
図1

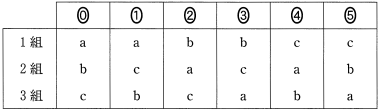
次の $\boxed{\text{ス}}$ に当てはまるものを, 下の⓪~⑤のうちから一つ選べ。

1組から3組の1回目のテストの結果と対応する図1の箱ひげ図の組合せは $\boxed{\text{ス}}$ である。

(2) 次の表2は, 1回目のテストの得点と2回目のテストの得点の標準偏差と共分散の値であり, 図2は, この2つのテストの得点の散布図と箱ひげ図である。ただし, 表2の数値は正確な値であり, 四捨五入されていないものとする。また,図2の散布図の点は重なっていることもある。

表2

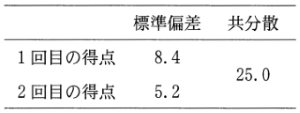
(共分散とは,1回目の得点の偏差と2回目の得点の偏差の積の平均値である。)

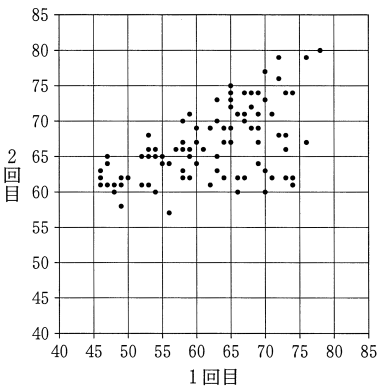
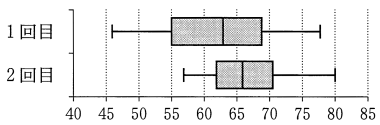
図2

次の $\boxed{\text{セ}}$, $\boxed{\text{ソ}}$ に当てはまるものを, 下の⓪~⑤のうちから一つずつ選べ。ただし, 解答の順序は問わない。

表2および図2の散布図と箱ひげ図について述べた文として誤っているものは, $\boxed{\text{セ}}$, $\boxed{\text{ソ}}$ である。

⓪ 四分位範囲は, 2回目の得点のほうが小さい。

① 表2から1回目の得点と2回目の得点の相関係数を計算すると, 0.65 以上になる。

② 1回目の得点が 55 点未満であった生徒は全員, 1回目の得点より2 回目の得点のほうが高い。

③ 2回目の得点が 70 点以上であった生徒は, 25 人以上いる。

④ 2回目の得点が1回目の得点より 10 点以上高い生徒は全員,1回目の得点が 55 点未満である。

⑤ 65点以上の得点をとった生徒の人数は, 1回目のテストより2回目のテストのほうが多い。

(3) 次の表3は, 1回目のテストの得点と3回目のテストの得点の平均点と標準偏差の値であり, 図3は, この2つのテストの得点の散布図である。ただし, 表3の数値は正確な値であり, 四捨五入されていないものとする。また, 図3の散布図の点は重なっていることもある。

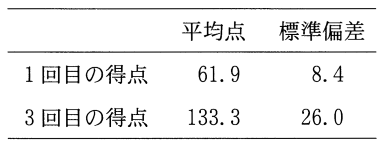
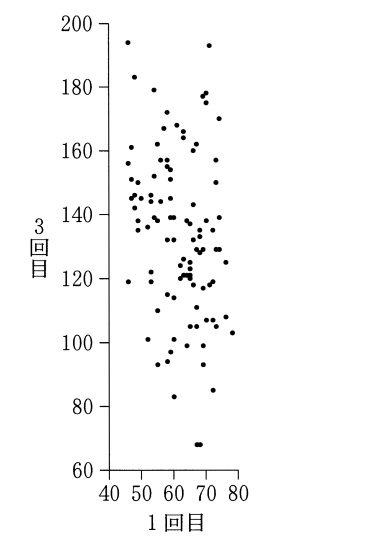
図3

ここで, 2つのテストの得点をそれぞれ, 次の計算式により新しい得点に換算した。

新しい得点 = $50+10\times\cfrac{\text{得点の偏差}}{標準偏差}\cdots\cdots$(＊)

次の $\boxed{\text{タ}}$ に当てはまるものを, 下の⓪~⑨のうちから一つ選べ。

1回目の得点を式(＊)により換算した新しい得点と3回目の得点を 式(＊)により換算した新しい得点の散布図は $\boxed{\text{タ}}$ である。

〔3〕A 組 $m$ 人とB 組 $n$ 人の生徒に対して行ったテストの得点を

A 組 $x_1, x_2,\cdots,x_m$

B 組 $y_1,y_2,\cdots,y_n$

と書く。各組の平均点を$\overline{x}$, $\overline{y}$, 分散を ${S_A}^2$, ${S_B}^2$ とする。また, A 組と B 組を合わせた $(m + n)$ 人の得点の平均点を $\overline{w}$, 分散を $S^2$ とする。これらの間に一般に成り立つ関係について調べる。

A 組の得点と $\overline{w}$ の差の2乗の和

$(x_1 – \overline{w})^2+(x_2-\overline{w})^2+\cdots+(x_m-\overline{w})^2$

を, $\overline{x}$, ${S_a}^2$, $\overline{w}$ を用いて表すと $\boxed{\text{チ}}$ である。ただし, ${S_A}^2$ は

${S_A}^2=\cfrac{1}{m}({x_1}^2+{x_2}^2+\cdots+{x_m}^2)-(\overline{x})^2$

で計算できる。$\boxed{\text{チ}}$ に当てはまるものを, 次の⓪~③のうちから一つ選べ。

⓪ ${S_A}^2+(\overline{x})^2+(\overline{w})^2$

① ${S_A}^2+(\overline{x}-\overline{w})^2$

② $m{S_A}^2+m\{(\overline{x})^2+(\overline{w})^2\}$

③ $m{S_A}^2+m(\overline{x}-\overline{w})^2$

A 組と B 組の生徒を合わせた $(m + n)$ 人の得点の分散 $S^2$ は $\boxed{\text{ツ}}$ に等しい。$\boxed{\text{ツ}}$ に当てはまるものを, 次の⓪~④のうちから一つ選べ。

⓪ $\cfrac{m{S_A}^2+n{S_B}^2+(m+n)\{(\overline{x}+\overline{y})^2-(\overline{w})^2\}}{m+n}$

① $\cfrac{m{S_A}^2+n{S_B}^2-(m+n)\{(\overline{x}+\overline{y})^2-(\overline{w})^2\}}{m+n}$

② $\cfrac{m{S_A}^2+n{S_B}^2-\{m(\overline{x})^2+n(\overline{y})^2\}+(m+n)(\overline{w})^2}{m+n}$

③ $\cfrac{m{S_A}^2+n{S_B}^2+m(\overline{x})^2+n(\overline{y})^2+(m+n)(\overline{w})^2}{m+n}$

④ $\cfrac{m{S_A}^2+n{S_B}^2+m(\overline{x})^2+n(\overline{y})^2-(m+n)(\overline{w})^2}{m+n}$