【スマホで読む・わかりやすい】センター数学IA2017本試【解説・正解・問題】

第5問　解答・解説

アイ 28　ウ エ 7 2　オカ キ 12 7

クケ　コ　21 5　サシ 60　ス セ ソ 2 3 3

タ チ ツ 4 3 3

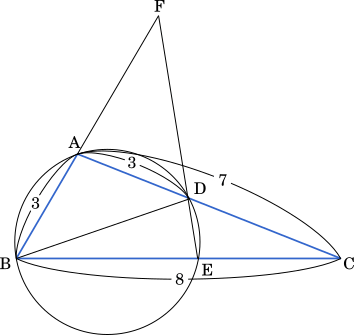
(1)

方べきの定理より

CD・CA ＝ CE・CB

7・4 ＝ CE・CB

したがって

BC・CE ＝ 28

・・・アイ

BC ＝ 8 だから

CE ＝ $\cfrac{28}{8}=\cfrac{7}{2}$

・・・ウエ

また，メネラウスの定理より

$\cfrac{\text{CE}}{\text{EB}}\cdot\cfrac{\text{BF}}{\text{FA}}\cdot\cfrac{\text{AD}}{\text{DC}}=1$

$\cfrac{\cfrac{7}{2}}{8-\cfrac{7}{2}}\cdot\cfrac{\text{BF}}{\text{FA}}\cdot\cfrac{3}{4}=1$

$\cfrac{7}{16-7}\cdot\cfrac{\text{BF}}{\text{FA}}\cdot\cfrac{3}{4}=1$

$\cfrac{7}{9}\cdot\cfrac{\text{BF}}{\text{FA}}\cdot\cfrac{3}{4}=1$

$\cfrac{\text{BF}}{\text{AF}}=\cfrac{12}{7}$

・・・オカキ

よって，BF：AF＝12：7

BF＝AB＋AF だから

AB＋AF：AF＝12：7

3＋AF：AF＝12：7

12AF＝7(3＋AF)

12AF＝21＋7AF

5AF＝21

AF＝$\cfrac{21}{5}$

・・・クケコ

(2)

余弦定理より

$7^2=3^2+8^2-2\cdot3\cdot8\cos$∠ABC

$49=9+64-48\cos$∠ABC

48 $\cos$∠ABC＝24

$\cos$∠ABC＝$\cfrac{1}{2}$

∠ABC＝60°

・・・サシ

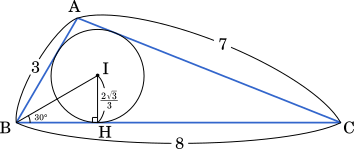
次に，△ABC の内接円の半径を求めるには，△ABC の面積を求めた上で，公式 $S=\cfrac{1}{2}r(a+b+c)$ を用いるとよい。

公式 $S=\cfrac{1}{2}bc\sin A$ より

$S=\cfrac{1}{2}\cdot3\cdot8\sin60\degree$

$=12\cdot\cfrac{\sqrt{3}}{2}=6\sqrt{3}$

よって

$6\sqrt{3}=\cfrac{1}{2}r(3+8+7)$

$6\sqrt{3}=9r$

$r=\cfrac{2\sqrt{3}}{3}$

・・・スセソ

次に，△ABC の内心を I とすると，∠IBC＝$\cfrac{1}{2}$∠ABC＝30°

I から BC に下ろした垂線と BC の交点を H とすると

$\cfrac{\text{IH}}{\text{BI}}=\sin$ 30°＝$\cfrac{1}{2}$

BI＝2IH

$=2\cdot\cfrac{2\sqrt{3}}{3}=\cfrac{4\sqrt{3}}{3}$

・・・タチツ

第5問　問題文

△ABC において, AB = 3, BC = 8, AC = 7 とする。

(1) 辺 AC 上に点 D を AD = 3 となるようにとり, △ABD の外接円と直線 BC の交点で B と異なるものを E とする。このとき, BC・CE = $\boxed{\text{アイ}}$ であるから, CE = $\cfrac{\boxed{\text{ウ}}}{\boxed{\text{エ}}}$ である。

直線 AB と直線 DE の交点を F とするとき, $\cfrac{\text{BF}}{\text{AF}}=\cfrac{\boxed{\text{オカ}}}{\boxed{\text{キ}}}$ であるから, AF = $\cfrac{\boxed{\text{クケ}}}{\boxed{\text{コ}}}$ である。

(2) ∠ABC = $\boxed{\text{サシ}}\degree$ である。△ABC の内接円の半径は $\cfrac{\boxed{\text{ス}}\sqrt{\boxed{\text{セ}}}}{\boxed{\text{ソ}}}$ であり, △ABC の内心を I とすると BI = $\cfrac{\boxed{\text{タ}}\sqrt{\boxed{\text{チ}}}}{\boxed{\text{ツ}}}$ である。